第7章 不等式 期末复习(2)不等式组 课件(共24张PPT)
文档属性
| 名称 | 第7章 不等式 期末复习(2)不等式组 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 954.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 16:54:26 | ||
图片预览








文档简介
(共24张PPT)
沪科版 七年级下册
第7章 不等式组 期末复习(2)
不等式组
一元一次不等式组的有关概念
一元一次不等式组的解法
确定不等式组的解集的两种方法
1.口诀法:求不等式组的解集时,可记住以下规律:同大取大;同小取小;大于小,小于大,取中间;大于大,小于小,是无解.
2.数轴法:运用数轴法确定不等式组的解集,就是将不等式组中的每一个不等式的解集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是此不等式组的解集.如果没有公共部分,则这个不等式组无解.
(一)不等式组典型例析
解下列不等式组:
3+x<3x-1 ②
2x+3>0 ①
(2)
②
5x-2<7x-4 ①
2x-1
3
3x+1
2
(1)
(3)
1<4x-3<5
>
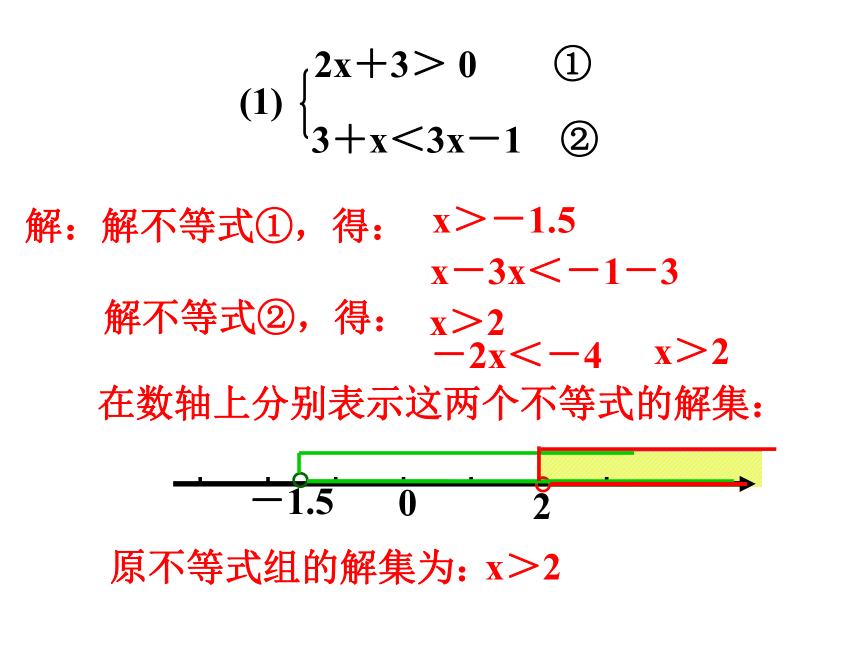
在数轴上分别表示这两个不等式的解集:
解不等式②,得:
解:解不等式①,得:
2
-1.5
0
原不等式组的解集为:
(1)
3+x<3x-1 ②
2x+3> 0 ①
x>-1.5
x>2
x>2
x-3x<-1-3
-2x<-4
x>2
在数轴上分别表示这两个不等式的解集:
解不等式②,得:
解:解不等式①,得:
1
-1
0
原不等式组无解
(2)
②
5x-2<7x-4 ①
x>1
x<-1
2x-1
3
>
3x+1
2
2(2x-1)>
3(3x+1)
4x-2 >
9x+3
4x-9x >
3+2
-5x >
5
在数轴上分别表示这两个不等式的解集:
解不等式②,得:
解不等式①,得:
2
1
0
原不等式组的解集为
(3)
x>1,
x<2.
1<4x-3<5
解:原不等式组可化为
4x-3>1
4x-3<5
1<x<2.
①
②
(二)不等式组的特殊解典型例析
1.已知不等式组的解集情况,求未知系数的
取值范围
例.已知关于x不等式组 无解,
求m的取值范围.
x-m>0 ①
x+3>2(x+2) ②
解:解不等式① ,得
解不等式②,得
x>m.
∵不等式组无解,
x<-1.
∴m≥-1.
∴ m的取值范围为m≥-1.
2.已知不等式组的解集,求未知系数的值
例.已知关于x不等式组 的
解集为1≤x<3,求a,b的取值范围.
x-a≥b+1 ①
x+2a>b ②
解:解不等式① ,得
解不等式②,得
x≥a+b+1.
∴不等式组的解集为a+b+1≤x<-2a+b.
x<-2a+b.
∴
∵不等式组的解集为-2≤x<3,
a+b+1=-2 ①
-2a+b=3 ②
∴
a=-2
b= -1.
3.已知不等式组的整数解的个数,求未知系数
的取值范围
例.已知关于x不等式组
只有3个整数解,求m的取值范围.
- <-1 ①
4(x-1)≤2(x-m) ②
解:解不等式① ,得
解不等式②,得
x>4.
∵不等式组只有3个整数解,
x≤2-m.
∴可以确定这3个整数解分别为5,6,7.
∴ 7≤2-m<8.
x-1
3
x
2
∴不等式组的解集为4<x≤2-m.
∴ -<m≤-5.
1. 不等式组 ,
的解集在数轴表示是( ).
x>1 ①
x-2>0 ②
2
1
0
2
1
0
2
1
0
2
1
0
C
D
A
B
B
(三)不等式组的 练习
1
2
3
-1
0A
-2
2. 不等式组 ,
的解集在数轴表示是( ).
2x+2>0 ①
-x≥-1 ②
1
2
3
-1
0B
-2
1
2
3
-1
0
-2
1
2
3
-1
0
-2
C
D
D
3.不等式组的解集在数轴上表示为,则原不等式组的解集为( )
A.x<2 B.x<3 C.x≤3 D.x≤2
A
4.若不等式组 有解,那么n的取值范围是( )
x>n
x< 8
A. n>8 B. n<8
C . n≤8 D. n≥8
B
5.不等式组 的整数解有( )
A.1个 B. 2个
C . 3个 D.无数个
-3x≤ x-8
2x-2< 6
B
1-x>0
x-a>0
6.已知关于x的不等式组
的整数解共有3个,则a的取值范围是 .
7.若关于x的一元一次不等式组
有解,则m的取值范围为 .
x-m>2
x-2m<0
-3≤a≤-2
8.若不等式组
无解,则a的取值范围是 .
5-2x≥-1
x-a>0
a≥3
m>2
3-2(x-2)≤9 ②
x-1
2
<1 ①
9.解不等式组 ,并把它的解集在数轴上表示出来.
2(1-x)+3>0 ①
x+2≥1 ②
(1)
(2)
将解集在数轴上表示为:
解:解不等式① ,得
解不等式②,得
-1x>-1.
x<2.5.
∴不等式组的解集为
2(1-x)+3>0 ①
x+2>1 ②
(1)
2.5
0
-1
将解集在数轴上表示为:
解:解不等式① ,得
解不等式②,得
2≤x<3.
x≥2.
x<3
∴不等式组的解集为
3
0
2
3-2(x-2)≤9 ②
x-1
2
<1 ①
(2)
10.求不等式组-2≤ ≤2的整数解.
1+2x
3
解不等式① ,得
解不等式②,得
∴不等式组的解集为:
解:
∴不等式组的整数解为:
不等式组可化为
1+2x
3
1+2x
3
≥-2 ①
≤2 ②
x≥-3.5
x≤2.5
x≤2.5
-3.5≤
± 3、
± 2、
± 1、
0.
11.如果不等式组 的解集为
x>4,那么a的取值范围是什么?
x> a
-x+2< x-6
解不等式①,得
x>4.
解:
①
解不等式②,得
x>a.
∵不等式组的解集为:
x>4.
∴a的取值范围是
a≤4.
②
12.方程组 的解 x,y都是正数,
求整数k.
3x+7y=k
2x+5y=20
解:
解方程组,得
x=
y=
5k-140
60-2k
∵ x>0,y>0,
5k-140>0
60-2k>0
∴
解这个不等式组,得
28<k<30
∴整数k为29.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级下册
第7章 不等式组 期末复习(2)
不等式组
一元一次不等式组的有关概念
一元一次不等式组的解法
确定不等式组的解集的两种方法
1.口诀法:求不等式组的解集时,可记住以下规律:同大取大;同小取小;大于小,小于大,取中间;大于大,小于小,是无解.
2.数轴法:运用数轴法确定不等式组的解集,就是将不等式组中的每一个不等式的解集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是此不等式组的解集.如果没有公共部分,则这个不等式组无解.
(一)不等式组典型例析
解下列不等式组:
3+x<3x-1 ②
2x+3>0 ①
(2)
②
5x-2<7x-4 ①
2x-1
3
3x+1
2
(1)
(3)
1<4x-3<5
>
在数轴上分别表示这两个不等式的解集:
解不等式②,得:
解:解不等式①,得:
2
-1.5
0
原不等式组的解集为:
(1)
3+x<3x-1 ②
2x+3> 0 ①
x>-1.5
x>2
x>2
x-3x<-1-3
-2x<-4
x>2
在数轴上分别表示这两个不等式的解集:
解不等式②,得:
解:解不等式①,得:
1
-1
0
原不等式组无解
(2)
②
5x-2<7x-4 ①
x>1
x<-1
2x-1
3
>
3x+1
2
2(2x-1)>
3(3x+1)
4x-2 >
9x+3
4x-9x >
3+2
-5x >
5
在数轴上分别表示这两个不等式的解集:
解不等式②,得:
解不等式①,得:
2
1
0
原不等式组的解集为
(3)
x>1,
x<2.
1<4x-3<5
解:原不等式组可化为
4x-3>1
4x-3<5
1<x<2.
①
②
(二)不等式组的特殊解典型例析
1.已知不等式组的解集情况,求未知系数的
取值范围
例.已知关于x不等式组 无解,
求m的取值范围.
x-m>0 ①
x+3>2(x+2) ②
解:解不等式① ,得
解不等式②,得
x>m.
∵不等式组无解,
x<-1.
∴m≥-1.
∴ m的取值范围为m≥-1.
2.已知不等式组的解集,求未知系数的值
例.已知关于x不等式组 的
解集为1≤x<3,求a,b的取值范围.
x-a≥b+1 ①
x+2a>b ②
解:解不等式① ,得
解不等式②,得
x≥a+b+1.
∴不等式组的解集为a+b+1≤x<-2a+b.
x<-2a+b.
∴
∵不等式组的解集为-2≤x<3,
a+b+1=-2 ①
-2a+b=3 ②
∴
a=-2
b= -1.
3.已知不等式组的整数解的个数,求未知系数
的取值范围
例.已知关于x不等式组
只有3个整数解,求m的取值范围.
- <-1 ①
4(x-1)≤2(x-m) ②
解:解不等式① ,得
解不等式②,得
x>4.
∵不等式组只有3个整数解,
x≤2-m.
∴可以确定这3个整数解分别为5,6,7.
∴ 7≤2-m<8.
x-1
3
x
2
∴不等式组的解集为4<x≤2-m.
∴ -<m≤-5.
1. 不等式组 ,
的解集在数轴表示是( ).
x>1 ①
x-2>0 ②
2
1
0
2
1
0
2
1
0
2
1
0
C
D
A
B
B
(三)不等式组的 练习
1
2
3
-1
0A
-2
2. 不等式组 ,
的解集在数轴表示是( ).
2x+2>0 ①
-x≥-1 ②
1
2
3
-1
0B
-2
1
2
3
-1
0
-2
1
2
3
-1
0
-2
C
D
D
3.不等式组的解集在数轴上表示为,则原不等式组的解集为( )
A.x<2 B.x<3 C.x≤3 D.x≤2
A
4.若不等式组 有解,那么n的取值范围是( )
x>n
x< 8
A. n>8 B. n<8
C . n≤8 D. n≥8
B
5.不等式组 的整数解有( )
A.1个 B. 2个
C . 3个 D.无数个
-3x≤ x-8
2x-2< 6
B
1-x>0
x-a>0
6.已知关于x的不等式组
的整数解共有3个,则a的取值范围是 .
7.若关于x的一元一次不等式组
有解,则m的取值范围为 .
x-m>2
x-2m<0
-3≤a≤-2
8.若不等式组
无解,则a的取值范围是 .
5-2x≥-1
x-a>0
a≥3
m>2
3-2(x-2)≤9 ②
x-1
2
<1 ①
9.解不等式组 ,并把它的解集在数轴上表示出来.
2(1-x)+3>0 ①
x+2≥1 ②
(1)
(2)
将解集在数轴上表示为:
解:解不等式① ,得
解不等式②,得
-1
x<2.5.
∴不等式组的解集为
2(1-x)+3>0 ①
x+2>1 ②
(1)
2.5
0
-1
将解集在数轴上表示为:
解:解不等式① ,得
解不等式②,得
2≤x<3.
x≥2.
x<3
∴不等式组的解集为
3
0
2
3-2(x-2)≤9 ②
x-1
2
<1 ①
(2)
10.求不等式组-2≤ ≤2的整数解.
1+2x
3
解不等式① ,得
解不等式②,得
∴不等式组的解集为:
解:
∴不等式组的整数解为:
不等式组可化为
1+2x
3
1+2x
3
≥-2 ①
≤2 ②
x≥-3.5
x≤2.5
x≤2.5
-3.5≤
± 3、
± 2、
± 1、
0.
11.如果不等式组 的解集为
x>4,那么a的取值范围是什么?
x> a
-x+2< x-6
解不等式①,得
x>4.
解:
①
解不等式②,得
x>a.
∵不等式组的解集为:
x>4.
∴a的取值范围是
a≤4.
②
12.方程组 的解 x,y都是正数,
求整数k.
3x+7y=k
2x+5y=20
解:
解方程组,得
x=
y=
5k-140
60-2k
∵ x>0,y>0,
5k-140>0
60-2k>0
∴
解这个不等式组,得
28<k<30
∴整数k为29.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
