青岛版七年级数学下册《平面图形的认识》复习课件(共21张PPT)
文档属性
| 名称 | 青岛版七年级数学下册《平面图形的认识》复习课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 16:03:45 | ||
图片预览







文档简介
(共21张PPT)
平面图形的认识
内角:
A
B
C
三个内角:如∠A,∠B,∠C
注意一个顶点上只有一个角时才能用顶点字母表示
顶点:
三个顶点,如顶点A,顶点B,顶点C.
边:
三条边 如 AB、BC、AC.
三角形中边 对面是顶点,顶点对面是边
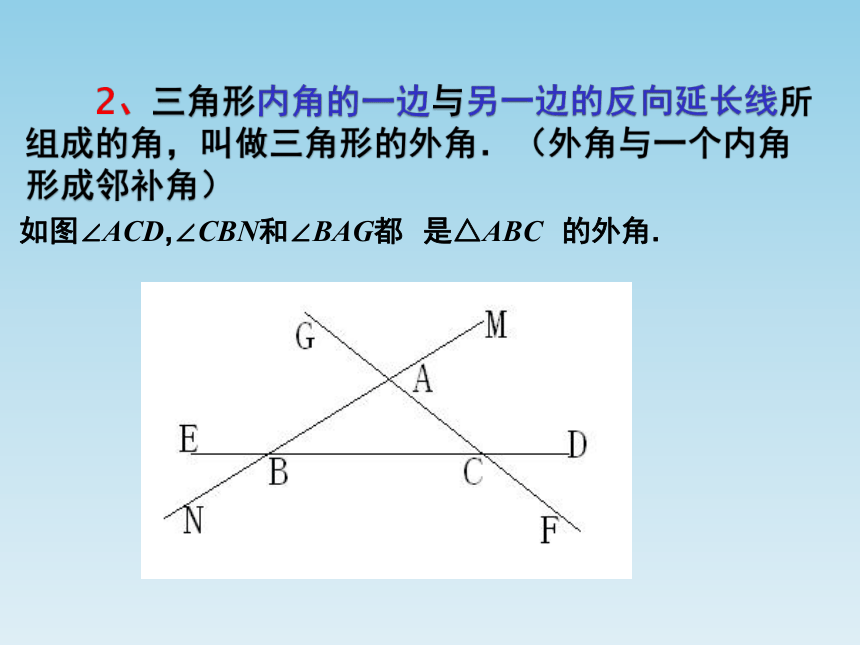
如图∠ACD,∠CBN和∠BAG都 是△ABC 的外角.
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
特别提示:等边三角形是特殊的等腰三角形.是底边和
腰相等的等腰三角形.等边必定等腰,等腰不一定等边.
锐角三角形
直角三角形
钝角三角形
在一个三角形中,最多有3个锐角,最多有1个直角,最多有1个钝角?
直角三角形通常用符号
“Rt△”表示.如Rt△ABC.
在直角三角形中,斜边最长
三角形的三边长分别为3㎝,8㎝,x㎝,且x为整数,那么x应满足5可能取的值共有5个,它们分别是6,7,8,9,10
例题:等腰三角形的周长为21cm,如果它的一边长为5cm,求其他两边的长.
提示5cm有可能是底边,也有可能是一条腰,分别讨论,但是5cm是腰形不成三角形.
A
B
C
D
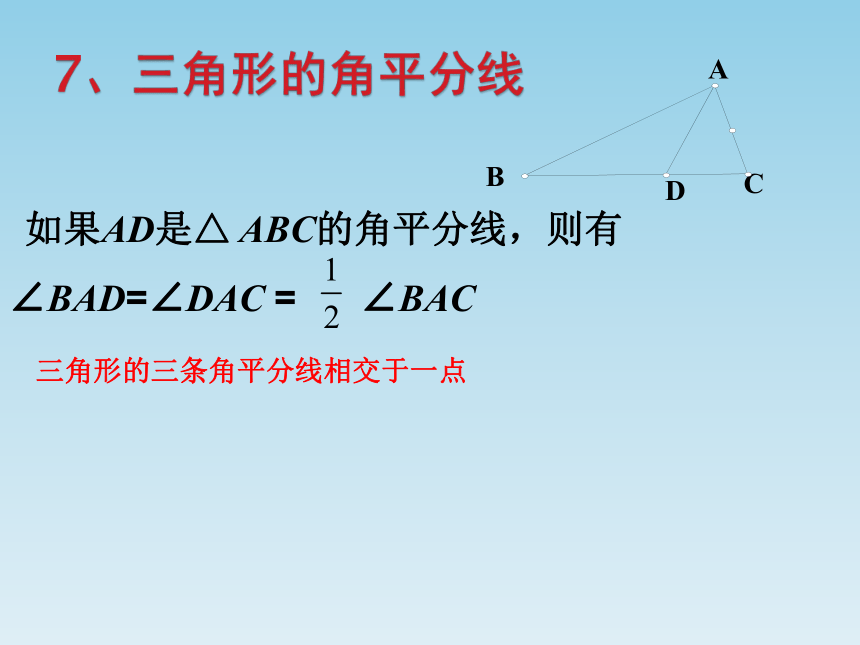
三角形的三条角平分线相交于一点
如果AD是△ ABC的角平分线,则有
∠BAD=∠DAC = ∠BAC
(1)顶点 对边 的中点所得线段 叫做三角形的中线.
A
B
C
D
如上图AD是△ABC 的中线,
则有( BD )=( DC )= BC;
△ABD的面积= △ADC的面积
三角形的三边中线相交于一点
从顶点向它的对边 画垂线,顶点和垂足所得线段 叫做三角形的高
A
B
C
D
三角形的三边的高不一定相交于一点
三角形的一个外角等于与它不相邻的两个内角的和.
10、三角形三个内角的和=180。
如图∠ACD=∠ B+ ∠A
重点例题课本151页例4
1、n边形从一个顶点出发的对角线的条数n-3
这些对角线把多边形分为n-2个三角形
n(n-3)
2
2、n边形总的对角线条数
3、在平面内,内角都相等,边也都相等的多边形叫做正多边形.
4、n边形内角和=(n-2) ·180°
正多边形一个内角=
5、任何多边形外角和都等于360°
正多边形一个外角=
1、点与圆的三种位置关系:
(1)点在圆上:点到圆心的距离等于半径
(2)点在圆内:点到圆心的距离小于半径
(3)点在圆外:点到圆心的距离大于半径
圆
2、连接圆上任意两点的线段叫做弦
经过圆心的弦叫做直径
直径是特殊的弦
3、能够重合的圆叫做等圆。等圆半径相同,面积相同,圆心不同
圆心相同、半径不等的圆叫做同心圆
1、已知线段a,作一条线段AB,使AB=a.
作法:
1.作射线AC
2.在射线AC上截取线段AB,AB 就是所要求作的线段
2.已知:∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:(1)作射线O′A′.
(2)以点 O 为圆心,以任意长为半径画弧,交OA于点C,交OB于点D.
(3)以点 O′为圆心,以 OC 长为半
径画弧,交O′A′于点C′.
(4)以点 O′ 为圆心,以 CD长为半
径画弧,交前面的弧于点D′.
(5)过点D′作射线 O′B′.
∠A′O′B′就是所求作的角.
3、已知两角和它们的夹边作三角形
例3 已知:∠1,∠2,线段m.
求作:△ABC,使BC=m, ∠B=∠1, ∠C=∠2
)
1
)
2
m
提示:先做夹边
4、已知两条边和它们的夹角作三角形
提示:先做夹角
5、已知三条边作三角形
平面图形的认识
内角:
A
B
C
三个内角:如∠A,∠B,∠C
注意一个顶点上只有一个角时才能用顶点字母表示
顶点:
三个顶点,如顶点A,顶点B,顶点C.
边:
三条边 如 AB、BC、AC.
三角形中边 对面是顶点,顶点对面是边
如图∠ACD,∠CBN和∠BAG都 是△ABC 的外角.
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
特别提示:等边三角形是特殊的等腰三角形.是底边和
腰相等的等腰三角形.等边必定等腰,等腰不一定等边.
锐角三角形
直角三角形
钝角三角形
在一个三角形中,最多有3个锐角,最多有1个直角,最多有1个钝角?
直角三角形通常用符号
“Rt△”表示.如Rt△ABC.
在直角三角形中,斜边最长
三角形的三边长分别为3㎝,8㎝,x㎝,且x为整数,那么x应满足5
例题:等腰三角形的周长为21cm,如果它的一边长为5cm,求其他两边的长.
提示5cm有可能是底边,也有可能是一条腰,分别讨论,但是5cm是腰形不成三角形.
A
B
C
D
三角形的三条角平分线相交于一点
如果AD是△ ABC的角平分线,则有
∠BAD=∠DAC = ∠BAC
(1)顶点 对边 的中点所得线段 叫做三角形的中线.
A
B
C
D
如上图AD是△ABC 的中线,
则有( BD )=( DC )= BC;
△ABD的面积= △ADC的面积
三角形的三边中线相交于一点
从顶点向它的对边 画垂线,顶点和垂足所得线段 叫做三角形的高
A
B
C
D
三角形的三边的高不一定相交于一点
三角形的一个外角等于与它不相邻的两个内角的和.
10、三角形三个内角的和=180。
如图∠ACD=∠ B+ ∠A
重点例题课本151页例4
1、n边形从一个顶点出发的对角线的条数n-3
这些对角线把多边形分为n-2个三角形
n(n-3)
2
2、n边形总的对角线条数
3、在平面内,内角都相等,边也都相等的多边形叫做正多边形.
4、n边形内角和=(n-2) ·180°
正多边形一个内角=
5、任何多边形外角和都等于360°
正多边形一个外角=
1、点与圆的三种位置关系:
(1)点在圆上:点到圆心的距离等于半径
(2)点在圆内:点到圆心的距离小于半径
(3)点在圆外:点到圆心的距离大于半径
圆
2、连接圆上任意两点的线段叫做弦
经过圆心的弦叫做直径
直径是特殊的弦
3、能够重合的圆叫做等圆。等圆半径相同,面积相同,圆心不同
圆心相同、半径不等的圆叫做同心圆
1、已知线段a,作一条线段AB,使AB=a.
作法:
1.作射线AC
2.在射线AC上截取线段AB,AB 就是所要求作的线段
2.已知:∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:(1)作射线O′A′.
(2)以点 O 为圆心,以任意长为半径画弧,交OA于点C,交OB于点D.
(3)以点 O′为圆心,以 OC 长为半
径画弧,交O′A′于点C′.
(4)以点 O′ 为圆心,以 CD长为半
径画弧,交前面的弧于点D′.
(5)过点D′作射线 O′B′.
∠A′O′B′就是所求作的角.
3、已知两角和它们的夹边作三角形
例3 已知:∠1,∠2,线段m.
求作:△ABC,使BC=m, ∠B=∠1, ∠C=∠2
)
1
)
2
m
提示:先做夹边
4、已知两条边和它们的夹角作三角形
提示:先做夹角
5、已知三条边作三角形
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
