青岛版七年级数学下册《平面图形的认识》复习课件(共21张PPT)
文档属性
| 名称 | 青岛版七年级数学下册《平面图形的认识》复习课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 16:05:39 | ||
图片预览







文档简介
(共21张PPT)
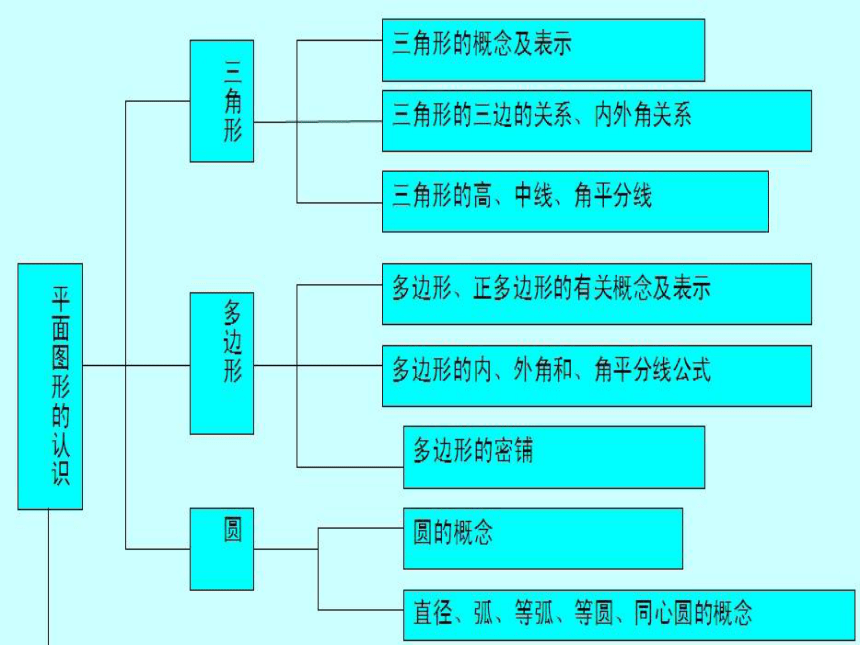
掌握三角形、多边形、圆的概念
经历对三角形、多边形、圆的有关性质的探索过程,掌握三角形的三边关系、内外角关系、多边形的内外角和公式、多边形的对角线公式,会用它们进行简单的有关计算.
经历多边形密铺条件的探索过程,尝试从不同角度解决问题。
会用基本尺规作图解决一些简单的作图问题.
复习目标
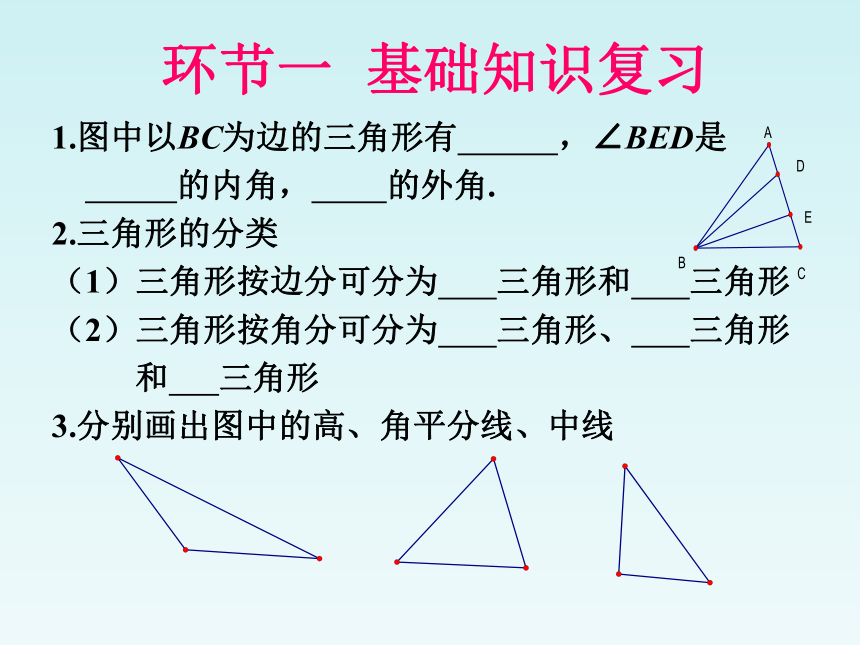
1.图中以BC为边的三角形有 ,∠BED是
的内角, 的外角.
2.三角形的分类
(1)三角形按边分可分为 三角形和 三角形
(2)三角形按角分可分为 三角形、 三角形
和 三角形
3.分别画出图中的高、角平分线、中线
环节一 基础知识复习
4.等腰三角形的两边分别是4和6,则周长为 .
5.多边形的内角和为 ,外角和为 ,对角线条数为 .
6.点与圆的位置关系有三种,分别是 , , .
如何判断?
环节二 专题讲解
题组一 三角形的三边关系
三角形的三边为a、b、c,用不等式表示三边关
系为: 利用这一性质可以解决如何构造三
角形的问题和求三角形边长的取值范围.
例1.三角形的最长边是10,另两边分别为x和4,周长为c,求x和c的取值范围。
解:已知三角形的两边长为10和4,那么第三边x的取值范围是10-4<x<10+4,即6<x<14,因为10是最长边,所以6<x≤10.所以周长c的取值范围是10+4+6<x≤10+10+4,故20<c≤24.
跟踪练习
1.有5条线段,长分别为1、2、3、4、5,以其中的三条为边,可以组成 个三角形,它们的边长分别为 .
2.已知,三角形的两边长分别为3和6,则第三边x的取值范围是 .
题组二:三角形的角平分线
例2.如图,△ABC中,BO、CO是角平分线.
若 ∠A=60°,则∠BOC= ,
若∠A=90°,则∠BOC= ,
若∠A=120°,则∠BOC= ,
猜想∠BOC和∠A之间的关系,并证明.
探究活动一:
若BO为∠ABC的平分线,CO为∠ABC的外角∠ACD的平分线,猜想∠BOC与∠A之间有何关系,请说明理由.
探究实验
若BO、CO分别为外角∠DBC和∠BCE的平分线,猜想∠BOC与∠A之间有何关系,请说明理由.
探究活动二
如图所示,△ABC的两个外角平分线相交于点D,若∠B=50°,则∠D=( )
A.60° B.80° C.65° D. 40°
训练反馈
题组三:三角形外角的性质
三角形的内角和是180°和三角形的一个外角等于和它不相邻的两个内角的和,是两个基本定理,可以解决许多有关三角形角度的问题.
例3.如图,已知∠B=∠CAB,∠ACD=
∠D,∠BAD=63°,求∠CAD的度数.
解:设∠CAD=x,则∠CAB=63°-x,
因为∠B=∠CAB,
∠ACD=∠D,所以∠B=∠CAB=63°-x,
∠ACD=∠D=2(63°-x)。在△ABD中,
由三角形的内角和等于180°,可得,
63°+(63°-x)+2(63°-x)=180°,解得x=24°,
所以∠CAD=24°.
B
C
A
D
反馈练习
1.求图中∠A+∠B+∠C+∠D+∠E的度数.
2.如图∠B=45°,∠A=30°,
∠C=25°,求∠ADC的大小.
A
B
E
C
D
B
A
C
D
题组四:多边形的性质
利用多边形的性质可以解决求边数和角的度数的问题.
例4.(1)若一个多边形的边数增加1,则这个多 边形的内角和增加 度.
(2)若将n边形的边数增加一倍,则它的内角和增加 度.
(3)已知多边形的边数恰好是从一个顶点出发的对角线数的2倍,求此多边形的边数与内角和.
实战演练
1.已知八边形的每个内角相等,求每个内角的度数。
2.已知正n边形的每个内角与其外角的差为90°,求边数n.
题组五:圆的性质
利用圆中直径与半径的关系及相关公式可以解决与圆有关的问题.
例5.如图,AB为⊙O的直径,CD为⊙O的弦,AB、
CD的延长线相交于点E,已知AB=2DE, ∠E
=18°,求∠AOC的度数.
分析:要求∠AOC的度数,由图知
∠AOC=∠C+∠E,故只需求出
∠C的度数,而由AB=2DE知DE与
半径相等,从而想到连结OD
构造等腰三角形ODE和等腰三角形OCD.
典题练习
1.已知⊙O的半径为10cm,根据下列点P到圆心的
距离,判定点P与圆的位置关系,并说明理由.
(1)8cm,(2)10cm,(3)12cm
2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,
则点P到⊙O上各点的最小距离是多少?
课堂小结
达标检测
1.已知等腰三角形的两边长为5和10,则第三边长为 ,周长为 .
2.有两根长为8cm、5cm的木棒,木工师傅要制作一个三角形,如果第三根木棒的长为整数,则第三根木棒的长度有哪几种选法?
3.如图,在直角△ABC中,∠C=90°,
AD平分∠BAC,BE平分∠ABC,
则∠APB= 度.
4.求图中∠A+∠B+∠C+∠D+∠E的度数.
5.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发地对角线的条数是( )
A.9 B.8 C.7 D.6
6.已知⊙ O的周长为10.
(1)若PO=5.5,则点P与圆的位置关系是什么
(2)若PO=4,则点P与圆的位置关系是什么
(3)若PO= ,则点P在圆上.
7.探究题:已知∠α、∠β,线段a,
求作:△ABC,使∠A=∠α,∠B=∠β,BC=a.
课本P.154
综合练习:5、7、8、10
作业
掌握三角形、多边形、圆的概念
经历对三角形、多边形、圆的有关性质的探索过程,掌握三角形的三边关系、内外角关系、多边形的内外角和公式、多边形的对角线公式,会用它们进行简单的有关计算.
经历多边形密铺条件的探索过程,尝试从不同角度解决问题。
会用基本尺规作图解决一些简单的作图问题.
复习目标
1.图中以BC为边的三角形有 ,∠BED是
的内角, 的外角.
2.三角形的分类
(1)三角形按边分可分为 三角形和 三角形
(2)三角形按角分可分为 三角形、 三角形
和 三角形
3.分别画出图中的高、角平分线、中线
环节一 基础知识复习
4.等腰三角形的两边分别是4和6,则周长为 .
5.多边形的内角和为 ,外角和为 ,对角线条数为 .
6.点与圆的位置关系有三种,分别是 , , .
如何判断?
环节二 专题讲解
题组一 三角形的三边关系
三角形的三边为a、b、c,用不等式表示三边关
系为: 利用这一性质可以解决如何构造三
角形的问题和求三角形边长的取值范围.
例1.三角形的最长边是10,另两边分别为x和4,周长为c,求x和c的取值范围。
解:已知三角形的两边长为10和4,那么第三边x的取值范围是10-4<x<10+4,即6<x<14,因为10是最长边,所以6<x≤10.所以周长c的取值范围是10+4+6<x≤10+10+4,故20<c≤24.
跟踪练习
1.有5条线段,长分别为1、2、3、4、5,以其中的三条为边,可以组成 个三角形,它们的边长分别为 .
2.已知,三角形的两边长分别为3和6,则第三边x的取值范围是 .
题组二:三角形的角平分线
例2.如图,△ABC中,BO、CO是角平分线.
若 ∠A=60°,则∠BOC= ,
若∠A=90°,则∠BOC= ,
若∠A=120°,则∠BOC= ,
猜想∠BOC和∠A之间的关系,并证明.
探究活动一:
若BO为∠ABC的平分线,CO为∠ABC的外角∠ACD的平分线,猜想∠BOC与∠A之间有何关系,请说明理由.
探究实验
若BO、CO分别为外角∠DBC和∠BCE的平分线,猜想∠BOC与∠A之间有何关系,请说明理由.
探究活动二
如图所示,△ABC的两个外角平分线相交于点D,若∠B=50°,则∠D=( )
A.60° B.80° C.65° D. 40°
训练反馈
题组三:三角形外角的性质
三角形的内角和是180°和三角形的一个外角等于和它不相邻的两个内角的和,是两个基本定理,可以解决许多有关三角形角度的问题.
例3.如图,已知∠B=∠CAB,∠ACD=
∠D,∠BAD=63°,求∠CAD的度数.
解:设∠CAD=x,则∠CAB=63°-x,
因为∠B=∠CAB,
∠ACD=∠D,所以∠B=∠CAB=63°-x,
∠ACD=∠D=2(63°-x)。在△ABD中,
由三角形的内角和等于180°,可得,
63°+(63°-x)+2(63°-x)=180°,解得x=24°,
所以∠CAD=24°.
B
C
A
D
反馈练习
1.求图中∠A+∠B+∠C+∠D+∠E的度数.
2.如图∠B=45°,∠A=30°,
∠C=25°,求∠ADC的大小.
A
B
E
C
D
B
A
C
D
题组四:多边形的性质
利用多边形的性质可以解决求边数和角的度数的问题.
例4.(1)若一个多边形的边数增加1,则这个多 边形的内角和增加 度.
(2)若将n边形的边数增加一倍,则它的内角和增加 度.
(3)已知多边形的边数恰好是从一个顶点出发的对角线数的2倍,求此多边形的边数与内角和.
实战演练
1.已知八边形的每个内角相等,求每个内角的度数。
2.已知正n边形的每个内角与其外角的差为90°,求边数n.
题组五:圆的性质
利用圆中直径与半径的关系及相关公式可以解决与圆有关的问题.
例5.如图,AB为⊙O的直径,CD为⊙O的弦,AB、
CD的延长线相交于点E,已知AB=2DE, ∠E
=18°,求∠AOC的度数.
分析:要求∠AOC的度数,由图知
∠AOC=∠C+∠E,故只需求出
∠C的度数,而由AB=2DE知DE与
半径相等,从而想到连结OD
构造等腰三角形ODE和等腰三角形OCD.
典题练习
1.已知⊙O的半径为10cm,根据下列点P到圆心的
距离,判定点P与圆的位置关系,并说明理由.
(1)8cm,(2)10cm,(3)12cm
2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,
则点P到⊙O上各点的最小距离是多少?
课堂小结
达标检测
1.已知等腰三角形的两边长为5和10,则第三边长为 ,周长为 .
2.有两根长为8cm、5cm的木棒,木工师傅要制作一个三角形,如果第三根木棒的长为整数,则第三根木棒的长度有哪几种选法?
3.如图,在直角△ABC中,∠C=90°,
AD平分∠BAC,BE平分∠ABC,
则∠APB= 度.
4.求图中∠A+∠B+∠C+∠D+∠E的度数.
5.一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发地对角线的条数是( )
A.9 B.8 C.7 D.6
6.已知⊙ O的周长为10.
(1)若PO=5.5,则点P与圆的位置关系是什么
(2)若PO=4,则点P与圆的位置关系是什么
(3)若PO= ,则点P在圆上.
7.探究题:已知∠α、∠β,线段a,
求作:△ABC,使∠A=∠α,∠B=∠β,BC=a.
课本P.154
综合练习:5、7、8、10
作业
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
