沪科版九年级下册25.1.2 正投影及其性质课件(共15张PPT)
文档属性
| 名称 | 沪科版九年级下册25.1.2 正投影及其性质课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 169.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 17:06:41 | ||
图片预览


文档简介
(共15张PPT)
第25章 投影与视图
25.1 第2课时 正投影及其性质
知识回顾
1. 什么是平行投影和中心投影?
2. 太阳发出的光照在物体上是 ,车灯发出的光照在物体上是 .
平行投影
中心投影
由平行光线形成的投影叫做平行投影.
由同一点 (点光源) 发出的光线形成的投影叫做中心投影.
获取新知
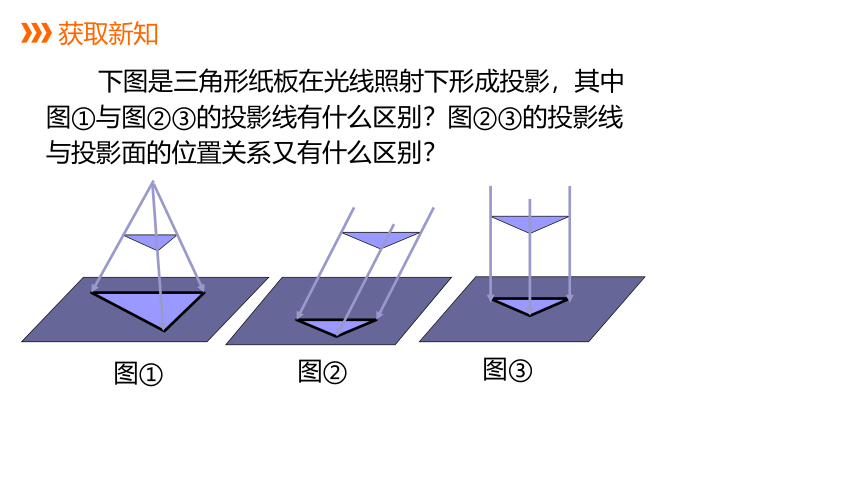
下图是三角形纸板在光线照射下形成投影,其中图①与图②③的投影线有什么区别?图②③的投影线与投影面的位置关系又有什么区别?
图①
图②
图③
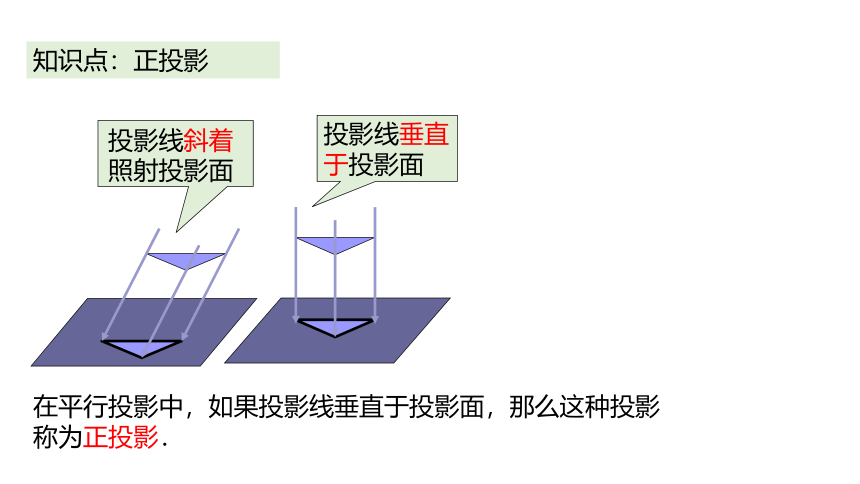
投影线斜着
照射投影面
投影线垂直于投影面
知识点:正投影
在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影.
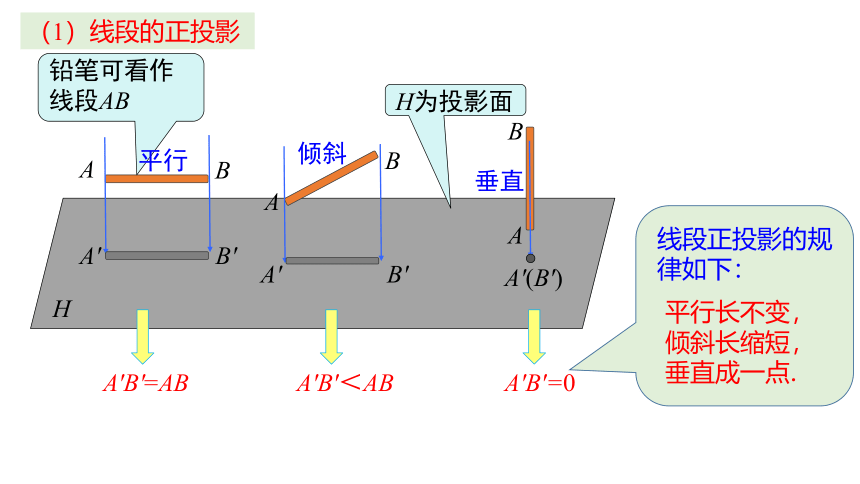
(1)线段的正投影
H
A
B
A
B
A
B
铅笔可看作线段AB
A'
B'
A'
B'
A'(B')
H为投影面
A'B'=AB
A'B'<AB
A'B'=0
平行
倾斜
垂直
线段正投影的规律如下:
平行长不变,
倾斜长缩短,
垂直成一点.
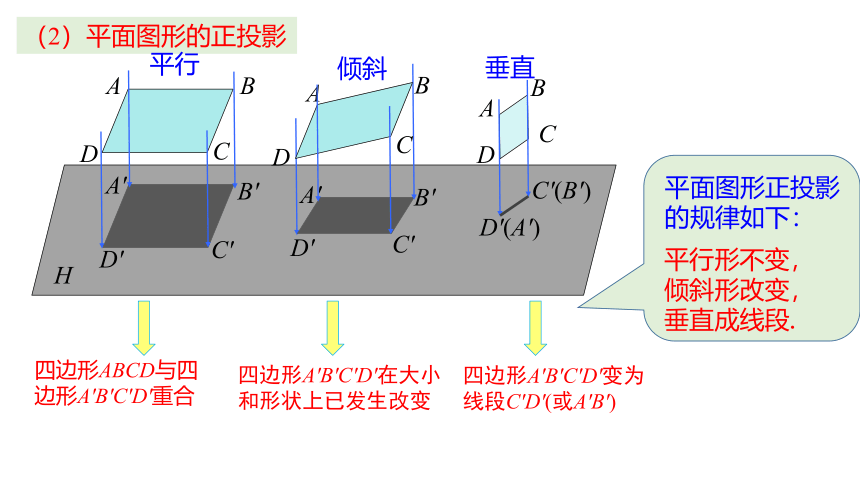
(2)平面图形的正投影
平面图形正投影的规律如下:
平行形不变,
倾斜形改变,
垂直成线段.
H
A
B
D
C
A'
B'
C'
D'
A'
B'
C'
D'
A
B
D
C
平行
倾斜
垂直
D'(A')
C'(B')
A
B
D
C
四边形ABCD与四边形A'B'C'D'重合
四边形A'B'C'D'在大小和形状上已发生改变
四边形A'B'C'D'变为线段C'D'(或A'B')
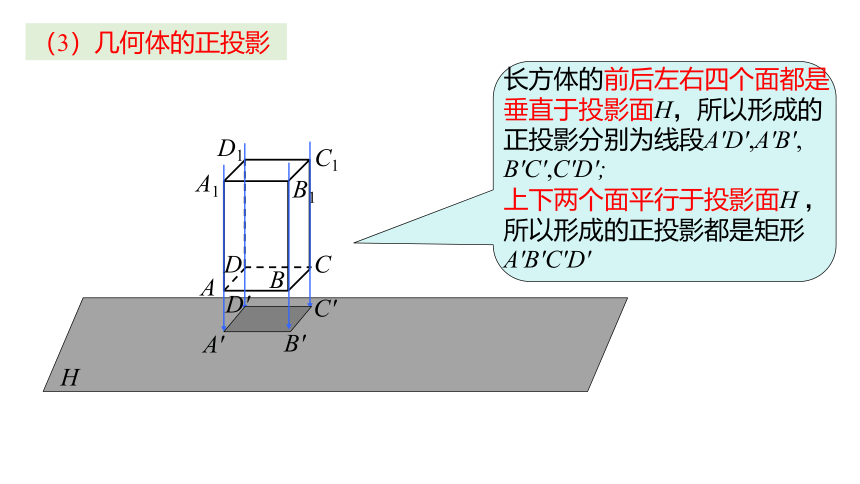
(3)几何体的正投影
H
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
长方体的前后左右四个面都是垂直于投影面H,所以形成的正投影分别为线段A'D',A'B', B'C',C'D';
上下两个面平行于投影面H ,所以形成的正投影都是矩形A'B'C'D'
H
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
规律如下:
一般地,一个几何体在一个平面上的正投影是一个平面图形.
一个几何体在一个平面上的正投影叫做这个几何体的视图.
例题讲解
例1 已知一根长为8 cm的木棒AB与投影面平行,投影线
垂直于投影面.
(1)求此时的影子A1B1的长度;
(2)如图是将木棒绕其端点A逆时针旋转30°后的示意图(此时平面ABB2A2垂直于投影面),求旋转后木棒的影子A2B2的长.
解:(1)因为木棒平行于投影面,所以A1B1=AB=8 cm,即此时的影子A1B1的长度为8 cm.
(2)如图,过点A作AH⊥BB2于点H.
因为AA2⊥A2B2,BB2⊥A2B2,
所以四边形AA2B2H为矩形,
所以AH=A2B2.
在Rt△ABH中,∠BAH=30°,AB=8 cm,
所以A2B2=AH=AB·cos 30°=8× =4 (cm).
即旋转后木棒的影子A2B2的长为4 cm.
例2 圆柱的轴截面平行于投影面 S,它的正投影是边长为 4的正方形,则这个圆柱的表面积是______.
4
4
圆柱的底面直径为4
圆柱的高为4
随堂演练
1. 下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
B
2. 木棒长为1.2m,则它的正投影的长一定( )
A. 大于1.2m B. 小于1.2m
C. 等于1.2m D. 小于或等于1.2m
D
3. 如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影是( )
D
课堂小结
正投影及其性质
线段的正投影
平面图形的正投影
几何体的正投影
平行长不变,倾斜长变短,垂直成一点
平行形不变,倾斜形改变,垂直成线段
平面图形
视图
第25章 投影与视图
25.1 第2课时 正投影及其性质
知识回顾
1. 什么是平行投影和中心投影?
2. 太阳发出的光照在物体上是 ,车灯发出的光照在物体上是 .
平行投影
中心投影
由平行光线形成的投影叫做平行投影.
由同一点 (点光源) 发出的光线形成的投影叫做中心投影.
获取新知
下图是三角形纸板在光线照射下形成投影,其中图①与图②③的投影线有什么区别?图②③的投影线与投影面的位置关系又有什么区别?
图①
图②
图③
投影线斜着
照射投影面
投影线垂直于投影面
知识点:正投影
在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影.
(1)线段的正投影
H
A
B
A
B
A
B
铅笔可看作线段AB
A'
B'
A'
B'
A'(B')
H为投影面
A'B'=AB
A'B'<AB
A'B'=0
平行
倾斜
垂直
线段正投影的规律如下:
平行长不变,
倾斜长缩短,
垂直成一点.
(2)平面图形的正投影
平面图形正投影的规律如下:
平行形不变,
倾斜形改变,
垂直成线段.
H
A
B
D
C
A'
B'
C'
D'
A'
B'
C'
D'
A
B
D
C
平行
倾斜
垂直
D'(A')
C'(B')
A
B
D
C
四边形ABCD与四边形A'B'C'D'重合
四边形A'B'C'D'在大小和形状上已发生改变
四边形A'B'C'D'变为线段C'D'(或A'B')
(3)几何体的正投影
H
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
长方体的前后左右四个面都是垂直于投影面H,所以形成的正投影分别为线段A'D',A'B', B'C',C'D';
上下两个面平行于投影面H ,所以形成的正投影都是矩形A'B'C'D'
H
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
规律如下:
一般地,一个几何体在一个平面上的正投影是一个平面图形.
一个几何体在一个平面上的正投影叫做这个几何体的视图.
例题讲解
例1 已知一根长为8 cm的木棒AB与投影面平行,投影线
垂直于投影面.
(1)求此时的影子A1B1的长度;
(2)如图是将木棒绕其端点A逆时针旋转30°后的示意图(此时平面ABB2A2垂直于投影面),求旋转后木棒的影子A2B2的长.
解:(1)因为木棒平行于投影面,所以A1B1=AB=8 cm,即此时的影子A1B1的长度为8 cm.
(2)如图,过点A作AH⊥BB2于点H.
因为AA2⊥A2B2,BB2⊥A2B2,
所以四边形AA2B2H为矩形,
所以AH=A2B2.
在Rt△ABH中,∠BAH=30°,AB=8 cm,
所以A2B2=AH=AB·cos 30°=8× =4 (cm).
即旋转后木棒的影子A2B2的长为4 cm.
例2 圆柱的轴截面平行于投影面 S,它的正投影是边长为 4的正方形,则这个圆柱的表面积是______.
4
4
圆柱的底面直径为4
圆柱的高为4
随堂演练
1. 下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
B
2. 木棒长为1.2m,则它的正投影的长一定( )
A. 大于1.2m B. 小于1.2m
C. 等于1.2m D. 小于或等于1.2m
D
3. 如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影是( )
D
课堂小结
正投影及其性质
线段的正投影
平面图形的正投影
几何体的正投影
平行长不变,倾斜长变短,垂直成一点
平行形不变,倾斜形改变,垂直成线段
平面图形
视图
