沪科版数学九年级下册26.2 第3课时 概率在实际生活中的应用 同步课件(共15张PPT)
文档属性
| 名称 | 沪科版数学九年级下册26.2 第3课时 概率在实际生活中的应用 同步课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 199.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 08:58:44 | ||
图片预览






文档简介
(共15张PPT)
第26章 概率初步
26.2 第3课时 概率在实际生活中的应用
例题讲解
例1 “石头、剪刀、布”是民间广为流传的一种游戏,游戏的两人每次做“石头”“剪刀”“布”三种手势中的一种,并 约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.现有甲、乙两人做这种游戏.
(1) 一次游戏中甲获胜、乙获胜的概率各是多少?
(2) 这种游戏对于两个人来说公平吗?
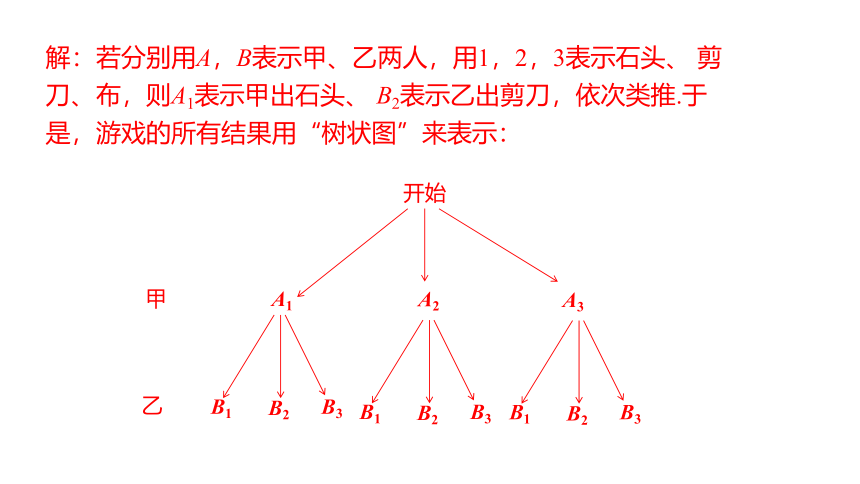
解:若分别用A,B表示甲、乙两人,用1,2,3表示石头、 剪刀、布,则A1表示甲出石头、 B2表示乙出剪刀,依次类推.于是,游戏的所有结果用“树状图”来表示:
开始
A1
A2
A3
B1
B3
B2
甲
乙
B1
B3
B2
B1
B3
B2
所有结果是9种,且出现的可能性相等.因此,一次游戏时:
甲获胜的结果有(A1,B2),(A2, B3),(A3, B1)这3 种,
故甲获胜的概率是 同理,乙获胜的概率也是
由(1)可知,这种游戏中,两人获胜的概率都是
机会均等,故游戏对于两人来说是公平的.
获取新知
【归纳总结】判断游戏公平性的方法:
游戏的公平性是通过比较游戏双方获胜的概率来判断的.
在条件相同的前提下,若参加游戏的每一方获胜的概率相等,则游戏公平,否则不公平.
例题讲解
例2 某人的密码箱密码由三个数字组成,每个数字都是从0 9中任选的.如果他忘记了自己设定的密码,求在一 次随机试验中他能打开箱子的概率.
解:设在一次随机试验中他能打开箱子的事件为A. 根据题意,在一次随机试验中选择的号码应是000 999中的任意一个3位数,所有可能出现的结果共有1000种, 且出现每一种结果的可能性相等.要能打开箱子, 即选择的号码与密码相同的结果只有1种,所以
P(A)=
答:在一次随机试验中他能打开箱子的概率为
例3 甲、乙两人要去风景区游玩,仅知道每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,但不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车,乙不乘第1辆车,并且仔细观察第2辆车的情况,如比第1辆车好,就乘第2辆车;如不比第1辆车好,就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?
解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:
(上中下),
(上下中),
(中上下),
(中下上),
(下上中),
(下中上).
假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲、乙两人分别会乘坐的汽车列表如下:
顺序 甲 乙
上中下
上下中
中上下
中下上
下上中
下中上
上
下
上
中
中
上
中
上
下
上
下
中
甲乘到上等、中等、下等3种汽车的概率都是 ;
乙乘到上等汽车的概率是 ,乙乘到中等汽车的概率是 ,乘坐下等汽车的概率只有
答:乙的乘车办法有利于乘上舒适度较好的车.
随堂演练
1.福彩3D“直选奖”玩法规则是:从由三个数字组成的数字组合000,001,002,…,998,999中任选一组数投注,当所选号码与开奖号码完全相同即中奖,则购买一注彩票中奖的概率为( )
D
2. 一个箱子中装有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后不放回,摸出黑色小球为赢,这个游戏( )
A.公平
B.不公平
C.先摸者赢的可能性大
D.后摸者赢的可能性大
A
3. 王红和刘芳两人玩转盘游戏,如图,把转盘A,B分别分成3等份,并在每一份内标上数字,游戏规则:转动两个转盘,停止后指针所指的两个数字之和为7时,王红胜;数字之和为8时,刘芳胜,那么这二人中获胜可能性较大的是________.
王红
4.端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其他均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.
(1)用画树状图或列表的方法表示出小悦拿到两个粽子的所有可能结果;
(2)请你计算小悦拿到的两个粽子都是肉馅的概率.
解:(1)将肉粽记为A,红枣粽子记为B,豆沙粽子记为C.画树状图如下:
(2)由(1)可得,小悦拿到的两个粽子都是肉馅的概率是
课堂小结
概率在实际生
活中的应用
彩票问题
游戏公平性
其他问题
直接列举法
列表法
画树状图法
每个参与的人获胜的概率彼此相等则游戏公平
第26章 概率初步
26.2 第3课时 概率在实际生活中的应用
例题讲解
例1 “石头、剪刀、布”是民间广为流传的一种游戏,游戏的两人每次做“石头”“剪刀”“布”三种手势中的一种,并 约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.现有甲、乙两人做这种游戏.
(1) 一次游戏中甲获胜、乙获胜的概率各是多少?
(2) 这种游戏对于两个人来说公平吗?
解:若分别用A,B表示甲、乙两人,用1,2,3表示石头、 剪刀、布,则A1表示甲出石头、 B2表示乙出剪刀,依次类推.于是,游戏的所有结果用“树状图”来表示:
开始
A1
A2
A3
B1
B3
B2
甲
乙
B1
B3
B2
B1
B3
B2
所有结果是9种,且出现的可能性相等.因此,一次游戏时:
甲获胜的结果有(A1,B2),(A2, B3),(A3, B1)这3 种,
故甲获胜的概率是 同理,乙获胜的概率也是
由(1)可知,这种游戏中,两人获胜的概率都是
机会均等,故游戏对于两人来说是公平的.
获取新知
【归纳总结】判断游戏公平性的方法:
游戏的公平性是通过比较游戏双方获胜的概率来判断的.
在条件相同的前提下,若参加游戏的每一方获胜的概率相等,则游戏公平,否则不公平.
例题讲解
例2 某人的密码箱密码由三个数字组成,每个数字都是从0 9中任选的.如果他忘记了自己设定的密码,求在一 次随机试验中他能打开箱子的概率.
解:设在一次随机试验中他能打开箱子的事件为A. 根据题意,在一次随机试验中选择的号码应是000 999中的任意一个3位数,所有可能出现的结果共有1000种, 且出现每一种结果的可能性相等.要能打开箱子, 即选择的号码与密码相同的结果只有1种,所以
P(A)=
答:在一次随机试验中他能打开箱子的概率为
例3 甲、乙两人要去风景区游玩,仅知道每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,但不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车,乙不乘第1辆车,并且仔细观察第2辆车的情况,如比第1辆车好,就乘第2辆车;如不比第1辆车好,就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?
解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:
(上中下),
(上下中),
(中上下),
(中下上),
(下上中),
(下中上).
假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲、乙两人分别会乘坐的汽车列表如下:
顺序 甲 乙
上中下
上下中
中上下
中下上
下上中
下中上
上
下
上
中
中
上
中
上
下
上
下
中
甲乘到上等、中等、下等3种汽车的概率都是 ;
乙乘到上等汽车的概率是 ,乙乘到中等汽车的概率是 ,乘坐下等汽车的概率只有
答:乙的乘车办法有利于乘上舒适度较好的车.
随堂演练
1.福彩3D“直选奖”玩法规则是:从由三个数字组成的数字组合000,001,002,…,998,999中任选一组数投注,当所选号码与开奖号码完全相同即中奖,则购买一注彩票中奖的概率为( )
D
2. 一个箱子中装有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后不放回,摸出黑色小球为赢,这个游戏( )
A.公平
B.不公平
C.先摸者赢的可能性大
D.后摸者赢的可能性大
A
3. 王红和刘芳两人玩转盘游戏,如图,把转盘A,B分别分成3等份,并在每一份内标上数字,游戏规则:转动两个转盘,停止后指针所指的两个数字之和为7时,王红胜;数字之和为8时,刘芳胜,那么这二人中获胜可能性较大的是________.
王红
4.端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其他均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.
(1)用画树状图或列表的方法表示出小悦拿到两个粽子的所有可能结果;
(2)请你计算小悦拿到的两个粽子都是肉馅的概率.
解:(1)将肉粽记为A,红枣粽子记为B,豆沙粽子记为C.画树状图如下:
(2)由(1)可得,小悦拿到的两个粽子都是肉馅的概率是
课堂小结
概率在实际生
活中的应用
彩票问题
游戏公平性
其他问题
直接列举法
列表法
画树状图法
每个参与的人获胜的概率彼此相等则游戏公平
