沪科版数学八年级下册 20.2平均数 课件 (共17张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 20.2平均数 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 585.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
20.2 数据的集中趋势与离散程度
1.数据的集中趋势
第一课时 平均数
1. 体育课上进行跳绳比赛,A组与B组各5名同学,他们一分钟的跳绳次数如下:
A: 155 162 176 140 150
B: 172 158 135 142 163
问: 哪一组的跳绳成绩好一些?
设疑引入
3.晓文上学期期中考试、期末考试数学成绩分别是88和96(百分制),如果规定期末总评时,期中考试成绩占30%,期末考试成绩占70%,晓文上学期的数学总评成绩为多少?
观察思考
上面的问题1中,我们已经收集到了数据
A: 155 162 176 140 150
B: 172 158 135 142 163
怎样分析数据,得出结论呢?
感悟新知
Ⅰ.平均数
().
对于一组数据,我们常用平均数来作为刻画它的集中趋势的一种方法.
一般地,如果有n 个数据
,,
那么,(…)就是这组数据的平均数,用“”表示,即
人们说“女性比男性寿命长”是依据什么得出的?
自主学习,合作交流
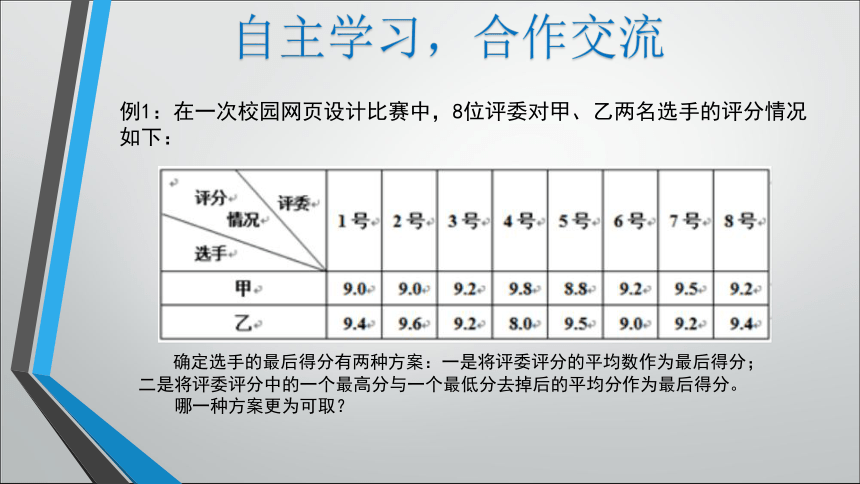
例1:在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委评分中的一个最高分与一个最低分去掉后的平均分作为最后得分。
哪一种方案更为可取?
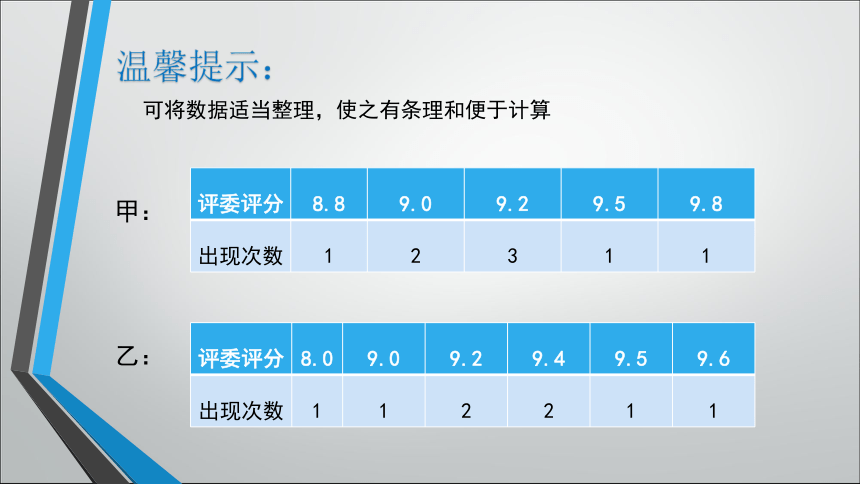
温馨提示:
可将数据适当整理,使之有条理和便于计算
评委评分 8.8 9.0 9.2 9.5 9.8
出现次数 1 2 3 1 1
评委评分 8.0 9.0 9.2 9.4 9.5 9.6
出现次数 1 1 2 2 1 1
甲:
乙:
解:按方案一计算甲、乙的最后得分为
这时,甲的成绩比乙高。
按方案二计算甲、乙的最后得分为
这时,乙的成绩比甲高。
议一议:
用平均数来刻画一组数据的集中趋势,容易受什么影响?
当我们用平均数来表示一组数据的集中趋势时,如果数据中出现一、两个极端数据,那么平均数对于这组数据所起的代表作用就会削弱,为了消除这种现象,可将少数极端数据去掉,只计算余下的数据的平均数.
小结:
合作探究
活动:探究加权平均数的概念及公式应用
例2:某校在招聘新教师时以考评成绩确定人选.甲、乙两位高校毕业生的各项考评成绩如下表:
(1)如果学校将教学设计、课堂教学和答辩按1:3:1的比例来计算各人的考评成绩,那么谁会被录用
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的成绩,那么谁会被录用?
议一议
2.例2中是用什么来表示各个指标的重要程度的?
1.各个指标的重要程度不一样,考评的结果一样吗?
感悟新知
II. 加权平均数
加权平均数计算公式:
其中,,…,分别表示数据,,…,出现的次数(如例1),或者表示数据,,…,在总结果中的比重(如例2),我们称其为各数据的权,叫做这n个数据的加权平均数。
思考与交流:
公式②与公式①有什么关系?
巩固练习:
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
计算这些运动员成绩的平均数(结果保留小数点后两位)。
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
2.某公司欲招聘一名公关人员,对甲、乙两位应试者进行了面试和笔试,
他们的成绩(百分制)如下表所示:
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁被录取?
(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的成绩,谁被录取?
应试者 面试 笔试
甲 86 90
乙 92 83
1.平均数计算:
平均数=各数据的和÷数据的个数
加权平均数=(各数据×该数据的权)的和÷总权数
总结
2.平均数的意义:
平均数是刻画一组数据的集中趋势的一种方法。
20.2 数据的集中趋势与离散程度
1.数据的集中趋势
第一课时 平均数
1. 体育课上进行跳绳比赛,A组与B组各5名同学,他们一分钟的跳绳次数如下:
A: 155 162 176 140 150
B: 172 158 135 142 163
问: 哪一组的跳绳成绩好一些?
设疑引入
3.晓文上学期期中考试、期末考试数学成绩分别是88和96(百分制),如果规定期末总评时,期中考试成绩占30%,期末考试成绩占70%,晓文上学期的数学总评成绩为多少?
观察思考
上面的问题1中,我们已经收集到了数据
A: 155 162 176 140 150
B: 172 158 135 142 163
怎样分析数据,得出结论呢?
感悟新知
Ⅰ.平均数
().
对于一组数据,我们常用平均数来作为刻画它的集中趋势的一种方法.
一般地,如果有n 个数据
,,
那么,(…)就是这组数据的平均数,用“”表示,即
人们说“女性比男性寿命长”是依据什么得出的?
自主学习,合作交流
例1:在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委评分中的一个最高分与一个最低分去掉后的平均分作为最后得分。
哪一种方案更为可取?
温馨提示:
可将数据适当整理,使之有条理和便于计算
评委评分 8.8 9.0 9.2 9.5 9.8
出现次数 1 2 3 1 1
评委评分 8.0 9.0 9.2 9.4 9.5 9.6
出现次数 1 1 2 2 1 1
甲:
乙:
解:按方案一计算甲、乙的最后得分为
这时,甲的成绩比乙高。
按方案二计算甲、乙的最后得分为
这时,乙的成绩比甲高。
议一议:
用平均数来刻画一组数据的集中趋势,容易受什么影响?
当我们用平均数来表示一组数据的集中趋势时,如果数据中出现一、两个极端数据,那么平均数对于这组数据所起的代表作用就会削弱,为了消除这种现象,可将少数极端数据去掉,只计算余下的数据的平均数.
小结:
合作探究
活动:探究加权平均数的概念及公式应用
例2:某校在招聘新教师时以考评成绩确定人选.甲、乙两位高校毕业生的各项考评成绩如下表:
(1)如果学校将教学设计、课堂教学和答辩按1:3:1的比例来计算各人的考评成绩,那么谁会被录用
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的成绩,那么谁会被录用?
议一议
2.例2中是用什么来表示各个指标的重要程度的?
1.各个指标的重要程度不一样,考评的结果一样吗?
感悟新知
II. 加权平均数
加权平均数计算公式:
其中,,…,分别表示数据,,…,出现的次数(如例1),或者表示数据,,…,在总结果中的比重(如例2),我们称其为各数据的权,叫做这n个数据的加权平均数。
思考与交流:
公式②与公式①有什么关系?
巩固练习:
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
计算这些运动员成绩的平均数(结果保留小数点后两位)。
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
2.某公司欲招聘一名公关人员,对甲、乙两位应试者进行了面试和笔试,
他们的成绩(百分制)如下表所示:
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁被录取?
(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的成绩,谁被录取?
应试者 面试 笔试
甲 86 90
乙 92 83
1.平均数计算:
平均数=各数据的和÷数据的个数
加权平均数=(各数据×该数据的权)的和÷总权数
总结
2.平均数的意义:
平均数是刻画一组数据的集中趋势的一种方法。
