6.4 生活中的圆周运动 导学案—2021-2022学年高一下学期物理人教版(2019)必修第二册(word版学案)
文档属性
| 名称 | 6.4 生活中的圆周运动 导学案—2021-2022学年高一下学期物理人教版(2019)必修第二册(word版学案) |  | |
| 格式 | zip | ||
| 文件大小 | 540.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-08 18:22:40 | ||
图片预览


文档简介
生活中的圆周运动
【学习目标】
1.会在具体问题中分析向心力的来源。
2.掌握应用牛顿运动定律解决匀速圆周运动问题的一般方法,会处理水平面内的匀速圆周运动问题。
【学习重难点】
会在具体问题中分析向心力的来源,并结合牛顿运动定律求解有关问题。
【学习过程】
【探究案】
探究一:火车转弯问题:火车转弯是一段圆周运动,需要有力来提供火车做圆周运动的向心力
【问题1】如果内、外轨是等高的,那么火车转弯时是如何获得向心力的?
【问题2】高速行驶的火车的轮缘与铁轨挤压,后果会怎样?
【问题3】那么应该如何解决这一实际问题?结合学过的知识加以讨论,提出可行的解决方案,并画出受力图,加以定性说明。
【问题4】火车转弯时的转弯半径为R,弯道的倾斜角度为α,火车转弯时的速度为多大时,才不至于对内、外轨道产生挤压?
A.外轨 内轨(低于、高于)。
B.此时火车的支持力FN的方向不再是竖直的,而是斜向弯道的内侧。
C.此时 的合力提供火车转弯所需的向心力。
D.转弯处要选择内外轨适当的高度差,使转弯时所需的向心力完全由
提供,这样外轨就不受轮缘的挤压了。
设内外轨的倾斜角度,火车转弯的半径为R,火车转弯的规定速度为v0,由图所示得向心力为= 由牛顿第二定律得:=m所以 = ,即火车转弯的规定速度
讨论:1.若火车速度小于,是内轨对火车轮缘有弹力还是外轮缘有弹力?
2.若火车速度大于,是内轨对火车轮缘有弹力还是外轮缘有弹力?
探究二:(圆锥摆)如图所示,用细线吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,,细线长度为L,小球运动时与竖直方向成角,求:
(1)小球运动的半径r
(2)小球向心力FN的大小
(3)小球线速度v的大小
(4)小球角速度w的大小
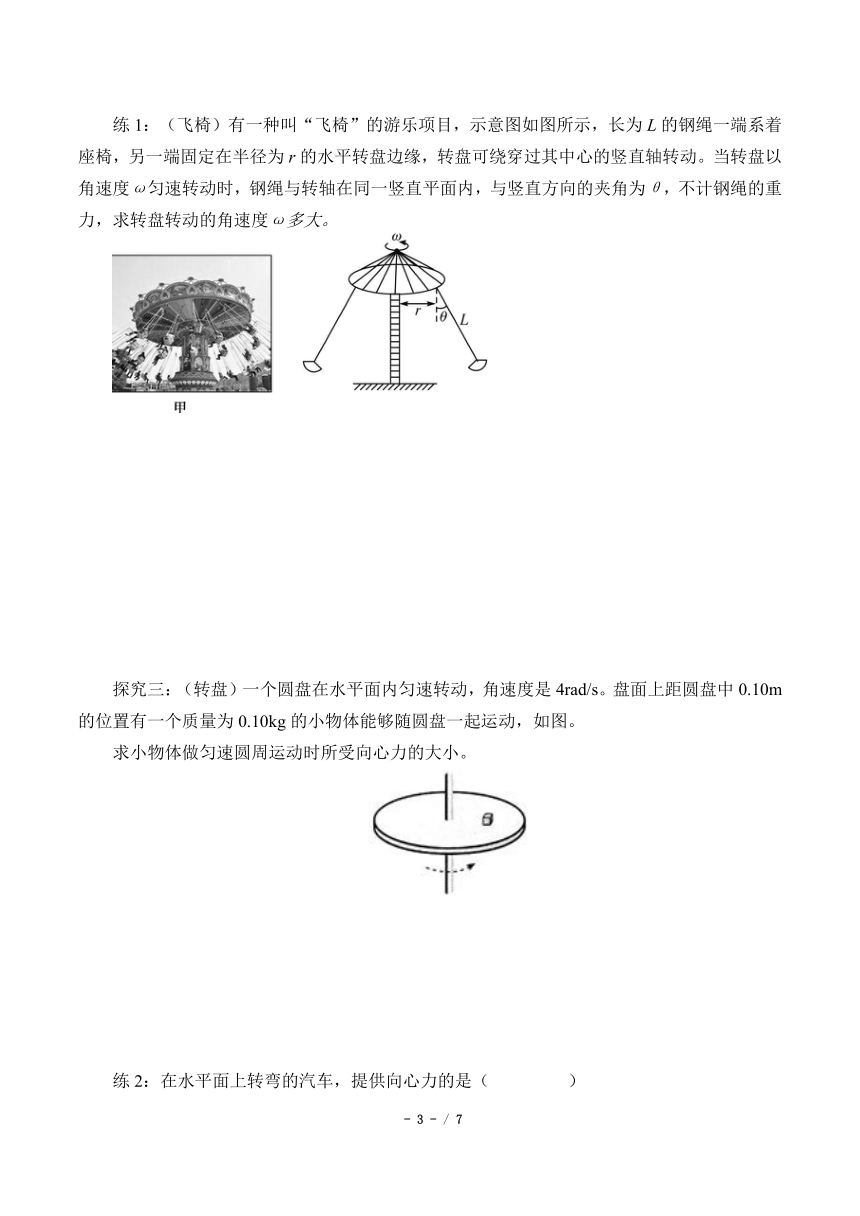
练1:(飞椅)有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动。当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω多大。
探究三:(转盘)一个圆盘在水平面内匀速转动,角速度是4rad/s。盘面上距圆盘中0.10m的位置有一个质量为0.10kg的小物体能够随圆盘一起运动,如图。
求小物体做匀速圆周运动时所受向心力的大小。
练2:在水平面上转弯的汽车,提供向心力的是( )
A.重力与支持力的合力 B.静摩擦力
C.滑动摩擦力 D.重力、支持力、牵引力的合力
练3:已知汽车的质量为m,所受最大静摩擦力是汽车重力的倍,已知重力加速度为g,汽车转弯时的安全行驶速度最大是多少?
探究四:(圆筒模型)如图所示,在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动,物体相对桶壁静止,则( )
A.物体受到重力、静摩擦力、弹力、向心力4个力的作用
B.物体所受向心力是物体所受的重力提供的
C.物体所受向心力是物体所受的弹力提供的
D.物体所受向心力是物体所受的静摩擦力提供的
若已知物体质量为m,圆筒半径为r,圆筒转动的角速度为w,则弹力大小为_______________。
练4:如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,小球紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,下列说法正确的是( )
A.重力提供向心力
B.筒壁支持力提供向心力
C.重力和筒壁支持力的合力提供向心力
D.小球受重力、支持力、向心力3个力的作用
训练案
1.【多选】在某转弯处,规定火车行驶的速率为v0,则下列说法中正确的是( )
A.当火车以速率v0行驶时,火车的重力与支持力的合力方向一定沿水平方向
B.当火车的速率v>v0时,火车对外轨有向外的侧向压力
C.当火车的速率v>v0时,火车对内轨有向内的挤压力
D.当火车的速率v2.如图所示,用细线吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,则小球受到的力有( )
A.重力、绳子的拉力、向心力
B.重力、绳子的拉力
C.重力
D.以上说法均不正确
3.【多选】如图所示的圆锥摆中,摆球A、B在同一水平面上作匀速圆周运动,关于A、B球的运动情况和受力情况,下列说法中正确的是( )
A.摆球A受重力、拉力和向心力的作用
B.摆球A受重力和拉力的作用
C.摆球A的向心力是重力和拉力的合力
D.摆球A、B做匀速圆周运动的线速度大小相等
【参考答案】
【探究案】
【问题4】
A.高于
C.重力和支持力
D.重力和支持力的合力
mgtanθ
mgtanθ m
讨论:1.【内轨】
2.【外轨】
探究二:
解题步骤:
1.明确研究对象
2.分析运动情况:①确定圆周所在平面(水平面、竖直平面)
②明确圆周运动的轨迹、圆心位置求圆周半径
3.进行受力分析,求出指向圆心的合力,即向心力
4.列方程(牛顿第二定律、牛顿第三定律)
5.求解
参考答案:
(1)小球运动的半径r=Lsin
(2)小球向心力FN=mgtan
(3)小球线速度v=
(4)小球角速度w=/( Lsin)
练1:答案:
探究三:答案:【0.16N】
练2:答案:B
练3:参考答案:
探究四:参考答案:C
若已知物体质量为m,圆筒半径为r,圆筒转动的角速度为w,则弹力大小为_mw2r_。
练4:参考答案:C
训练案
1.ABD
2.无
3.BC
2 / 2
【学习目标】
1.会在具体问题中分析向心力的来源。
2.掌握应用牛顿运动定律解决匀速圆周运动问题的一般方法,会处理水平面内的匀速圆周运动问题。
【学习重难点】
会在具体问题中分析向心力的来源,并结合牛顿运动定律求解有关问题。
【学习过程】
【探究案】
探究一:火车转弯问题:火车转弯是一段圆周运动,需要有力来提供火车做圆周运动的向心力
【问题1】如果内、外轨是等高的,那么火车转弯时是如何获得向心力的?
【问题2】高速行驶的火车的轮缘与铁轨挤压,后果会怎样?
【问题3】那么应该如何解决这一实际问题?结合学过的知识加以讨论,提出可行的解决方案,并画出受力图,加以定性说明。
【问题4】火车转弯时的转弯半径为R,弯道的倾斜角度为α,火车转弯时的速度为多大时,才不至于对内、外轨道产生挤压?
A.外轨 内轨(低于、高于)。
B.此时火车的支持力FN的方向不再是竖直的,而是斜向弯道的内侧。
C.此时 的合力提供火车转弯所需的向心力。
D.转弯处要选择内外轨适当的高度差,使转弯时所需的向心力完全由
提供,这样外轨就不受轮缘的挤压了。
设内外轨的倾斜角度,火车转弯的半径为R,火车转弯的规定速度为v0,由图所示得向心力为= 由牛顿第二定律得:=m所以 = ,即火车转弯的规定速度
讨论:1.若火车速度小于,是内轨对火车轮缘有弹力还是外轮缘有弹力?
2.若火车速度大于,是内轨对火车轮缘有弹力还是外轮缘有弹力?
探究二:(圆锥摆)如图所示,用细线吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,,细线长度为L,小球运动时与竖直方向成角,求:
(1)小球运动的半径r
(2)小球向心力FN的大小
(3)小球线速度v的大小
(4)小球角速度w的大小
练1:(飞椅)有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动。当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω多大。
探究三:(转盘)一个圆盘在水平面内匀速转动,角速度是4rad/s。盘面上距圆盘中0.10m的位置有一个质量为0.10kg的小物体能够随圆盘一起运动,如图。
求小物体做匀速圆周运动时所受向心力的大小。
练2:在水平面上转弯的汽车,提供向心力的是( )
A.重力与支持力的合力 B.静摩擦力
C.滑动摩擦力 D.重力、支持力、牵引力的合力
练3:已知汽车的质量为m,所受最大静摩擦力是汽车重力的倍,已知重力加速度为g,汽车转弯时的安全行驶速度最大是多少?
探究四:(圆筒模型)如图所示,在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动,物体相对桶壁静止,则( )
A.物体受到重力、静摩擦力、弹力、向心力4个力的作用
B.物体所受向心力是物体所受的重力提供的
C.物体所受向心力是物体所受的弹力提供的
D.物体所受向心力是物体所受的静摩擦力提供的
若已知物体质量为m,圆筒半径为r,圆筒转动的角速度为w,则弹力大小为_______________。
练4:如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,小球紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,下列说法正确的是( )
A.重力提供向心力
B.筒壁支持力提供向心力
C.重力和筒壁支持力的合力提供向心力
D.小球受重力、支持力、向心力3个力的作用
训练案
1.【多选】在某转弯处,规定火车行驶的速率为v0,则下列说法中正确的是( )
A.当火车以速率v0行驶时,火车的重力与支持力的合力方向一定沿水平方向
B.当火车的速率v>v0时,火车对外轨有向外的侧向压力
C.当火车的速率v>v0时,火车对内轨有向内的挤压力
D.当火车的速率v
A.重力、绳子的拉力、向心力
B.重力、绳子的拉力
C.重力
D.以上说法均不正确
3.【多选】如图所示的圆锥摆中,摆球A、B在同一水平面上作匀速圆周运动,关于A、B球的运动情况和受力情况,下列说法中正确的是( )
A.摆球A受重力、拉力和向心力的作用
B.摆球A受重力和拉力的作用
C.摆球A的向心力是重力和拉力的合力
D.摆球A、B做匀速圆周运动的线速度大小相等
【参考答案】
【探究案】
【问题4】
A.高于
C.重力和支持力
D.重力和支持力的合力
mgtanθ
mgtanθ m
讨论:1.【内轨】
2.【外轨】
探究二:
解题步骤:
1.明确研究对象
2.分析运动情况:①确定圆周所在平面(水平面、竖直平面)
②明确圆周运动的轨迹、圆心位置求圆周半径
3.进行受力分析,求出指向圆心的合力,即向心力
4.列方程(牛顿第二定律、牛顿第三定律)
5.求解
参考答案:
(1)小球运动的半径r=Lsin
(2)小球向心力FN=mgtan
(3)小球线速度v=
(4)小球角速度w=/( Lsin)
练1:答案:
探究三:答案:【0.16N】
练2:答案:B
练3:参考答案:
探究四:参考答案:C
若已知物体质量为m,圆筒半径为r,圆筒转动的角速度为w,则弹力大小为_mw2r_。
练4:参考答案:C
训练案
1.ABD
2.无
3.BC
2 / 2
