沪科版数学八年级下册 18.2 勾股定理的逆定理 课件(共10张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.2 勾股定理的逆定理 课件(共10张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览


文档简介
(共10张PPT)
18.2 勾股定理的逆定理
活动1:
O
A
B
如果数轴上的点A,B分别表示数 , , 两点A,B间的距离记作 ,那么 =
对于平面上的两点A,B间的距离,又如何计算它们的距离呢?
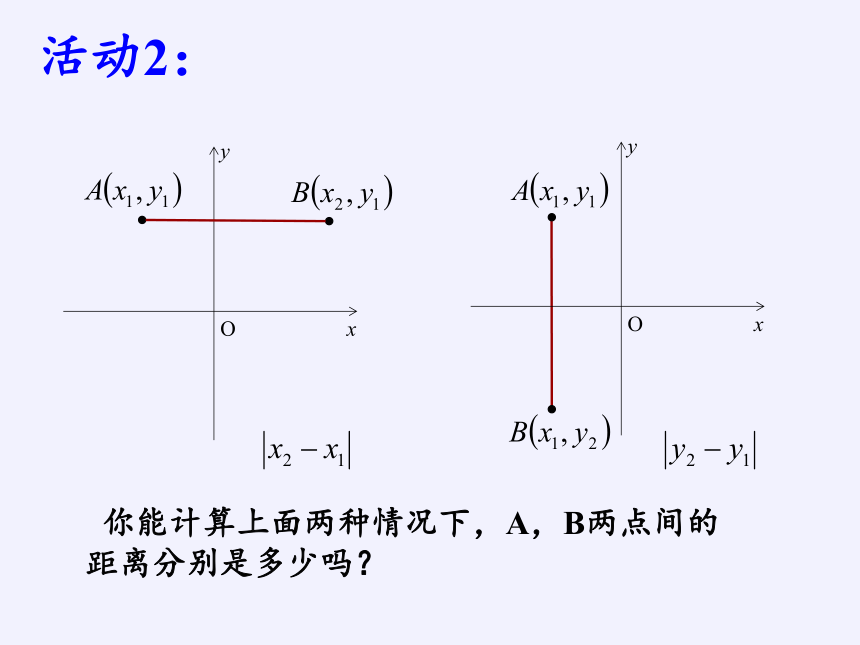
活动2:
O
y
x
O
y
x
你能计算上面两种情况下,A,B两点间的距离分别是多少吗?
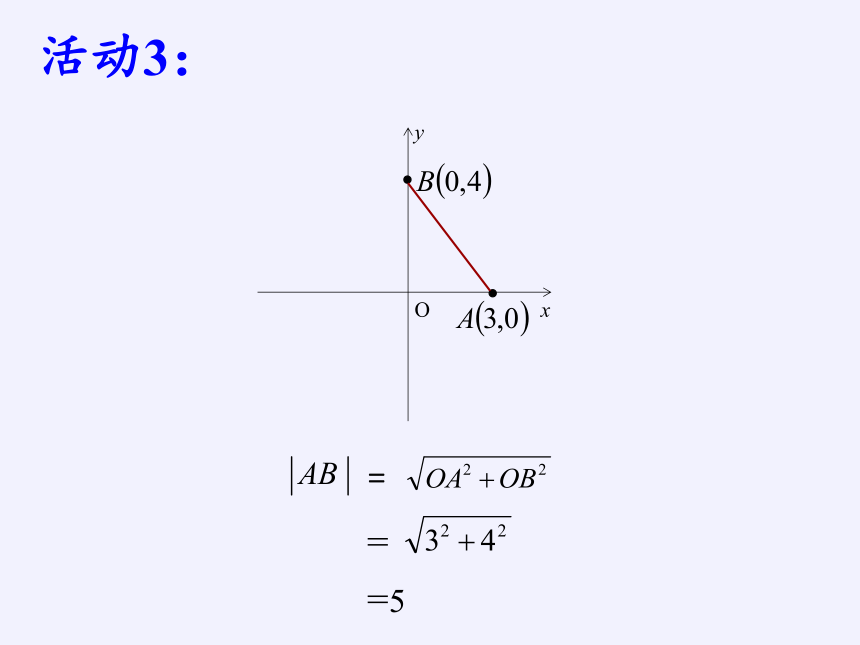
活动3:
O
y
x
=
=
=5
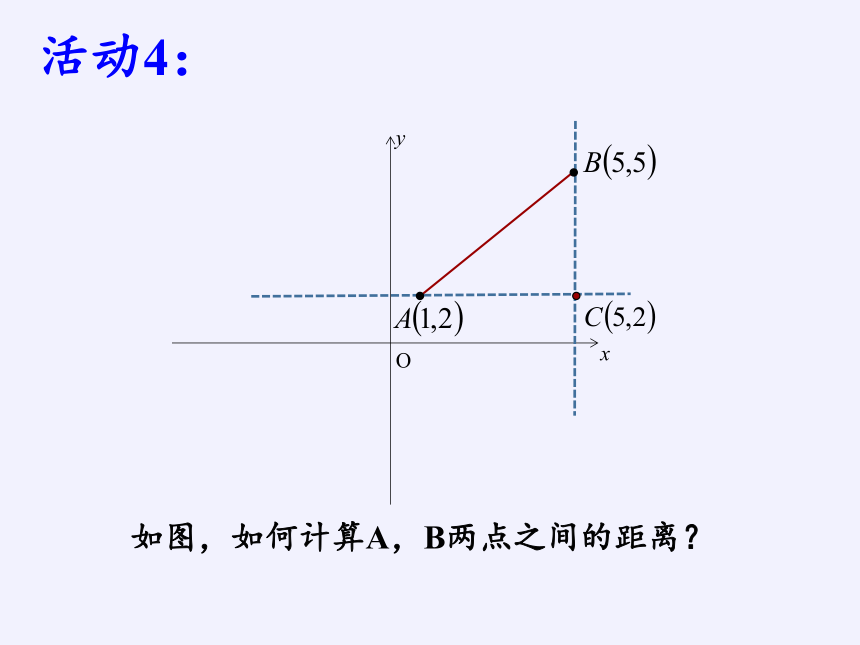
活动4:
O
y
x
如图,如何计算A,B两点之间的距离?
活动5:
O
y
x
作AC⊥x轴,BC⊥y轴,AC与BC相较于点C,
则△ABC是直角三角形,且∠C=90°,
∵ =
=
∴ = + = +
∴ =
(两点之间的距离公式)
练一练:
1、求下列两点之间的距离:
(1)A(-1,2),B(-5,-6)
(2)A(1,-5),B(7,3)
2、有两艘船在海上航行,测得两船的位置分别是(30,50),(105,150),求两船之间的距离。
通过本节课学习,你有什么收获?
作业设计
必做题:
1.求下列两点之间的距离:
(1)A(-1,0),B(2,3)
(2)A(4,3) ,B(7,-1)
2.已知△ABC的三个顶点是A(-2,0),B(2,0),C(1, ),试判断△ABC的形状。
作业设计
选做题:
坐标平面内有一点A(2, ),O为原点,在x轴上找一点B,使以O,A,B为顶点的三角形为等腰三角形,写出点B的坐标。
谢 谢
18.2 勾股定理的逆定理
活动1:
O
A
B
如果数轴上的点A,B分别表示数 , , 两点A,B间的距离记作 ,那么 =
对于平面上的两点A,B间的距离,又如何计算它们的距离呢?
活动2:
O
y
x
O
y
x
你能计算上面两种情况下,A,B两点间的距离分别是多少吗?
活动3:
O
y
x
=
=
=5
活动4:
O
y
x
如图,如何计算A,B两点之间的距离?
活动5:
O
y
x
作AC⊥x轴,BC⊥y轴,AC与BC相较于点C,
则△ABC是直角三角形,且∠C=90°,
∵ =
=
∴ = + = +
∴ =
(两点之间的距离公式)
练一练:
1、求下列两点之间的距离:
(1)A(-1,2),B(-5,-6)
(2)A(1,-5),B(7,3)
2、有两艘船在海上航行,测得两船的位置分别是(30,50),(105,150),求两船之间的距离。
通过本节课学习,你有什么收获?
作业设计
必做题:
1.求下列两点之间的距离:
(1)A(-1,0),B(2,3)
(2)A(4,3) ,B(7,-1)
2.已知△ABC的三个顶点是A(-2,0),B(2,0),C(1, ),试判断△ABC的形状。
作业设计
选做题:
坐标平面内有一点A(2, ),O为原点,在x轴上找一点B,使以O,A,B为顶点的三角形为等腰三角形,写出点B的坐标。
谢 谢
