鲁教版(五四制)数学六年级下册 6.5 整式的乘法-第一课时 课件(共14张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级下册 6.5 整式的乘法-第一课时 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
整式的乘法
第一课时
学习目标
知识与技能目标:
1.理解并掌握单项式的乘法法则。
2.能够熟练地进行单项式的乘法计算过程与方法目标:由问题情境,引发思考,通过合作探究,归纳单项式乘法的法则。
情感态度与价值观目标:
培养学生的归纳、概括能力、运算能力以及分析问题的思维方法。
重点:
单项式的乘法法则及其应用
难点:
理解运算法则及其探究过程
学习重难点
(1)预习。
(2)思考:单项式与单项式相乘可化为几个步骤?
(3)预习作业:
什么是单项式?
单项式由哪几部分组成?
(一)预习准备
1.下列代数式中,哪些是单项式?哪些不是?
√
√
√
√
【注意】
①单项式必须是整式,即分母中不能含有字母 。
②单项式的形式必须是数字与字母乘积的形式,不含有“+”或“-”号。
温故知新
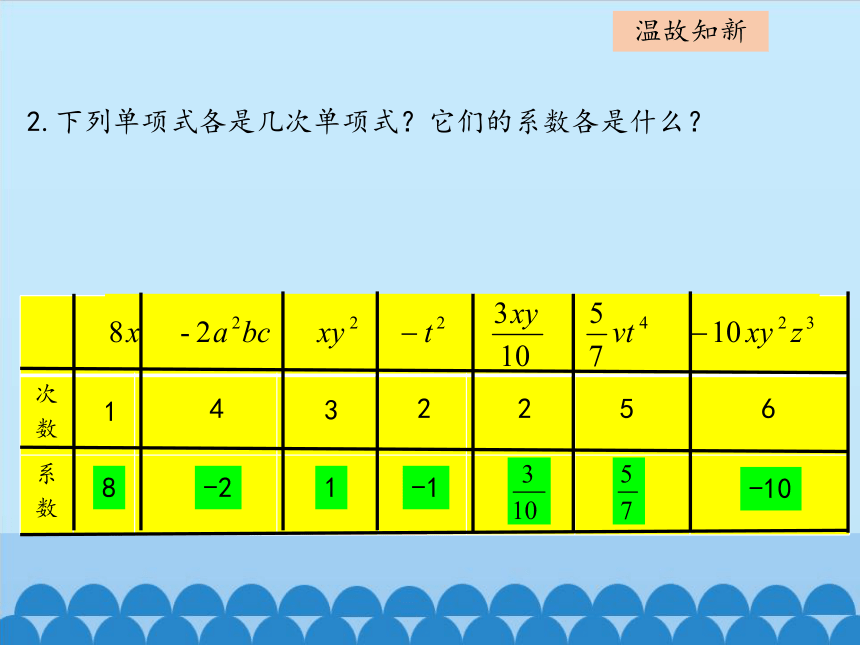
2.下列单项式各是几次单项式?它们的系数各是什么?
次 数
系 数
1
8
4
-2
3
1
2
-1
2
5
6
-10
温故知新
3.下列各式是什么运算?运算结果呢?
(1) =__________
(2) =__________
(3) =__ ____________
(4) =________ ____________
温故知新
(1) 等于什么?你是怎样计算的?
=
单项式
单项式
合作探究
例1:利用乘法交换律、结合律以及前面所学的幂的运算性质计算下列单项式乘以单项式。
知识应用
解:
知识应用
方法:1.系数:系数与系数相乘,作为积的系数。
注意:先确定系数的符号,再把系数的绝对值相乘。
2.字母:相同的字母与相同的字母相乘——同底数幂的乘法(底数不变,指数相加)。
注意:只在一个单项式中出现过的字母,连同它的指数作为积的一个因式)。
如果是多个单项式相乘__ __________
方法同样适用
且结果仍为单项式。
方法归纳
随堂练习
计算:
(1)5x3·2x2y; (2)(-3ɑb)·(-4b2);
(3)3ɑb·2ɑ; (4)yz·2y2z2;
(5)(2x2y)3·(-4xy2);(6) ɑ3b·6ɑ5b2c·(-ɑc2)2.
方法:1.系数:系数与系数相乘,作为积的系数。
注意:先确定系数的符号,再把系数的绝对值相乘。
2.字母:相同的字母与相同的字母相乘——同底数幂的乘法(底数不变,指数相加)。
注意:只在一个单项式中出现过的字母,连同它的指数作为积的一个因式。
如果是多个单项式相乘________ ____
方法同样适用
且结果仍为单项式
▲注意:有乘方,应先算乘方
回顾小结
谢 谢
整式的乘法
第一课时
学习目标
知识与技能目标:
1.理解并掌握单项式的乘法法则。
2.能够熟练地进行单项式的乘法计算过程与方法目标:由问题情境,引发思考,通过合作探究,归纳单项式乘法的法则。
情感态度与价值观目标:
培养学生的归纳、概括能力、运算能力以及分析问题的思维方法。
重点:
单项式的乘法法则及其应用
难点:
理解运算法则及其探究过程
学习重难点
(1)预习。
(2)思考:单项式与单项式相乘可化为几个步骤?
(3)预习作业:
什么是单项式?
单项式由哪几部分组成?
(一)预习准备
1.下列代数式中,哪些是单项式?哪些不是?
√
√
√
√
【注意】
①单项式必须是整式,即分母中不能含有字母 。
②单项式的形式必须是数字与字母乘积的形式,不含有“+”或“-”号。
温故知新
2.下列单项式各是几次单项式?它们的系数各是什么?
次 数
系 数
1
8
4
-2
3
1
2
-1
2
5
6
-10
温故知新
3.下列各式是什么运算?运算结果呢?
(1) =__________
(2) =__________
(3) =__ ____________
(4) =________ ____________
温故知新
(1) 等于什么?你是怎样计算的?
=
单项式
单项式
合作探究
例1:利用乘法交换律、结合律以及前面所学的幂的运算性质计算下列单项式乘以单项式。
知识应用
解:
知识应用
方法:1.系数:系数与系数相乘,作为积的系数。
注意:先确定系数的符号,再把系数的绝对值相乘。
2.字母:相同的字母与相同的字母相乘——同底数幂的乘法(底数不变,指数相加)。
注意:只在一个单项式中出现过的字母,连同它的指数作为积的一个因式)。
如果是多个单项式相乘__ __________
方法同样适用
且结果仍为单项式。
方法归纳
随堂练习
计算:
(1)5x3·2x2y; (2)(-3ɑb)·(-4b2);
(3)3ɑb·2ɑ; (4)yz·2y2z2;
(5)(2x2y)3·(-4xy2);(6) ɑ3b·6ɑ5b2c·(-ɑc2)2.
方法:1.系数:系数与系数相乘,作为积的系数。
注意:先确定系数的符号,再把系数的绝对值相乘。
2.字母:相同的字母与相同的字母相乘——同底数幂的乘法(底数不变,指数相加)。
注意:只在一个单项式中出现过的字母,连同它的指数作为积的一个因式。
如果是多个单项式相乘________ ____
方法同样适用
且结果仍为单项式
▲注意:有乘方,应先算乘方
回顾小结
谢 谢
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
