人教版数学九年级下册第二十九章 数学活动 课件(共15张PPT)
文档属性
| 名称 | 人教版数学九年级下册第二十九章 数学活动 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
数学活动
——三视图、展开图与立体图
如何画一个物体的三视图?
新课导入
如何根据几何体的三视图制作模型?
如何设计并制作笔筒?
这节课我们来完成这三个活动?
活动1 观察物体,画出三视图
请同学们按小组围成一桌,从自己的角度观察桌上摆放的物体,画出它们的三视图。
请根据你看到的三视图说出物体的形状.如果说得不对,请考虑改进所画的图,或者与同学交流。
推进新课
活动2 设计几何体,制作模型
(1)每个同学设计一个几何体,画出三视图。 (2)同桌之间交换三视图图纸,按照手中的三
视图制作几何体模型。
(3)同桌之间交流,看一看,作出的模型与设
计者的想法一致吗?
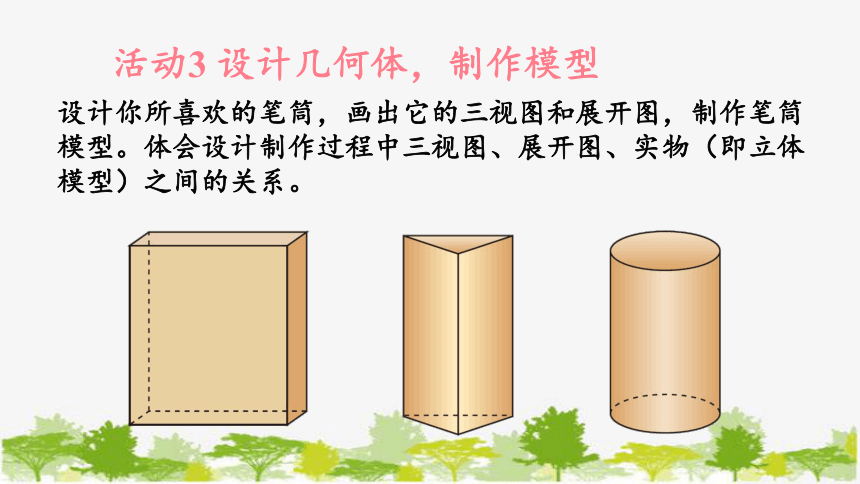
活动3 设计几何体,制作模型
设计你所喜欢的笔筒,画出它的三视图和展开图,制作笔筒模型。体会设计制作过程中三视图、展开图、实物(即立体模型)之间的关系。
基础巩固
1.下面四个图形中,是三棱柱的平面展开图的是( )
A B C D
A
随堂演练
2.有一实物如图所示,那么它的主视图是( )
A B C D
B
3.左图是一个小正方体的展开图,小正方体从如右图所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( )
A.和 B.谐 C.社 D.会
D
综合应用
4.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标数据(单位:mm),计算这个立体图形的表面积。
解: S底=6×8×2=96(mm2);
S侧=4×2×2+4×4×2
+6×2×2+8×2×2=104(mm2);
S表=96+104=200(mm2).
一个几何体及它的左视图、表面展开图如图所示。(几何体的上、下底面均为梯形)(单位:cm)
(1)写出这个几何体的名称;
(2)计算这个几何体的侧面积和左视图的面积。
解:(1)几何体是四棱柱
(2)S侧=13×(5+12+5+6)=364(cm2)
S左= (cm2)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
数学活动
——三视图、展开图与立体图
如何画一个物体的三视图?
新课导入
如何根据几何体的三视图制作模型?
如何设计并制作笔筒?
这节课我们来完成这三个活动?
活动1 观察物体,画出三视图
请同学们按小组围成一桌,从自己的角度观察桌上摆放的物体,画出它们的三视图。
请根据你看到的三视图说出物体的形状.如果说得不对,请考虑改进所画的图,或者与同学交流。
推进新课
活动2 设计几何体,制作模型
(1)每个同学设计一个几何体,画出三视图。 (2)同桌之间交换三视图图纸,按照手中的三
视图制作几何体模型。
(3)同桌之间交流,看一看,作出的模型与设
计者的想法一致吗?
活动3 设计几何体,制作模型
设计你所喜欢的笔筒,画出它的三视图和展开图,制作笔筒模型。体会设计制作过程中三视图、展开图、实物(即立体模型)之间的关系。
基础巩固
1.下面四个图形中,是三棱柱的平面展开图的是( )
A B C D
A
随堂演练
2.有一实物如图所示,那么它的主视图是( )
A B C D
B
3.左图是一个小正方体的展开图,小正方体从如右图所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( )
A.和 B.谐 C.社 D.会
D
综合应用
4.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标数据(单位:mm),计算这个立体图形的表面积。
解: S底=6×8×2=96(mm2);
S侧=4×2×2+4×4×2
+6×2×2+8×2×2=104(mm2);
S表=96+104=200(mm2).
一个几何体及它的左视图、表面展开图如图所示。(几何体的上、下底面均为梯形)(单位:cm)
(1)写出这个几何体的名称;
(2)计算这个几何体的侧面积和左视图的面积。
解:(1)几何体是四棱柱
(2)S侧=13×(5+12+5+6)=364(cm2)
S左= (cm2)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
