高中数学 2.3.2 离散型随机变量的方差 ppt
文档属性
| 名称 | 高中数学 2.3.2 离散型随机变量的方差 ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 75.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-11 00:00:00 | ||
图片预览





文档简介
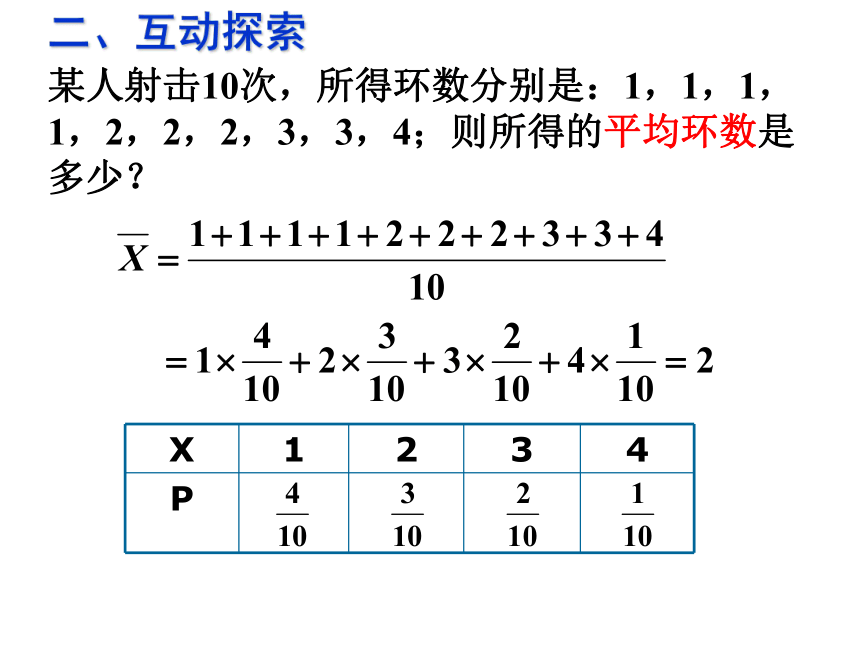
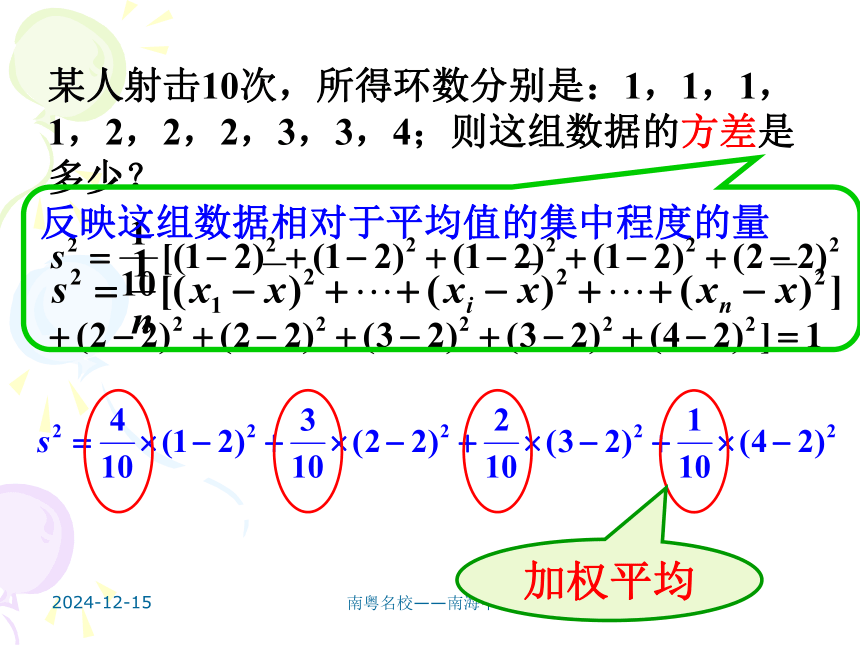
课件14张PPT。离散型随机变量的方差2019-1-19南粤名校——南海中学一、复习回顾1、离散型随机变量的数学期望2、数学期望的性质数学期望是反映离散型随机变量的平均水平2019-1-19南粤名校——南海中学某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?二、互动探索某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则这组数据的方差是多少?反映这组数据相对于平均值的集中程度的量加权平均2019-1-19南粤名校——南海中学离散型随机变量取值的方差一般地,若离散型随机变量X的概率分布为:则称为随机变量X的方差。称为随机变量X的标准差。它们都是反映离散型随机变量偏离于均值的平均程度的量,它们的值越小,则随机变量偏离于均值的平均程度越小,即越集中于均值。2019-1-19南粤名校——南海中学三、基础训练1、已知随机变量X的分布列求DX和σX。 解:2019-1-19南粤名校——南海中学2、若随机变量X满足P(X=c)=1,其中c为常数,求EX和DX。解:离散型随机变量X的分布列为:EX=c×1=cDX=(c-c)2×1=02019-1-19南粤名校——南海中学四、方差的应用例:甲、乙两名射手在同一条件下射击,所得环数X1, X2分布列如下:用击中环数的期望与方差分析比较两名射手的射击水平。解:表明甲、乙射击的平均水平没有差别,在多次射击中平均得分差别不会很大,但甲通常发挥比较稳定,多数得分在9环,而乙得分比较分散,近似平均分配在8-10环。2019-1-19南粤名校——南海中学问题1:如果你是教练,你会派谁参加比赛呢?问题2:如果其他对手的射击成绩都在8环左右,应派哪一名选手参赛?问题3:如果其他对手的射击成绩都在9环左右,应派哪一名选手参赛?2019-1-19南粤名校——南海中学练习:有甲乙两个单位都愿意聘用你,而你能获得如下信息:根据工资待遇的差异情况,你愿意选择哪家单位?2019-1-19南粤名校——南海中学解:在两个单位工资的数学期望相等的情况下,如果认为自己能力很强,应选择工资方差大的单位,即乙单位;如果认为自己能力不强,就应选择工资方差小的单位,即甲单位。2019-1-19南粤名校——南海中学五、几个常用公式:2019-1-19南粤名校——南海中学相关练习:3、有一批数量很大的商品,其中次品占1%,现从中任意地连续取出200件商品,设其次品数为X,求EX和DX。117100.82,1.982019-1-19南粤名校——南海中学六、课堂小结1、离散型随机变量取值的方差、标准差及意义2、记住几个常见公式2019-1-19南粤名校——南海中学
