第三章概率复习课件
图片预览







文档简介
课件21张PPT。概率复习课考点:1、随机事件
2、频率与概率的意义
3、古典概型
4、几何概型
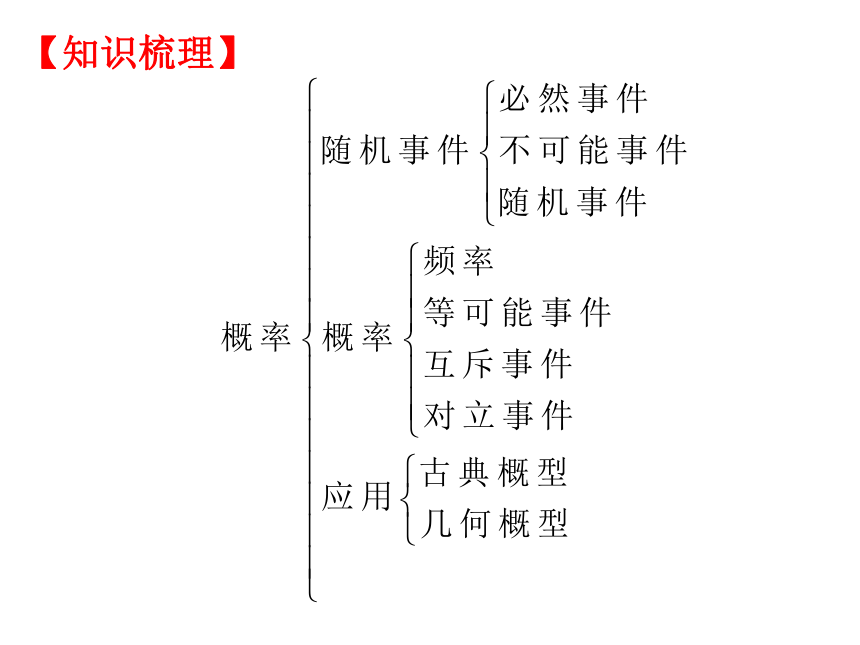
5、互斥事件和对立事件【知识梳理】【范例点睛】
例1.有三个人,每个人都以相同的概率被分配到四个房间中的每一间.试求(1)三个人都分配到同一房间的概率;(2)至少有两个人分配到同一房间的概率.思路点拨:∵三个人以同样的概率分配到每个房间,而三个人中每个人都可以分配到四个房间中的每一间,∴共有4×4×4=64种方法.
(1)三个人分配到同一房间有4中分法,故由等可能事件的概率可知,所求的概率为.(2)设事件A为”至少有两人分配到同一房间”,则事件A的对立事件为”三个人分配到三个不同的房间”.∵三个人分配到三个不同房间共有 不同种方法,∴ ,
∴
练习1: 有两个人在一座10层大楼的底层进入电梯,设他们中的每一个人自第二层起在每一层离开是等可能的,求两人在不同层离开的概率;
2、将一枚质地均匀的硬币连续抛掷4次,求出现“2次正面朝上,2次反面朝上”的概率3、鞋柜有4双不同的鞋,随机取出4只,试求下列事件的概率:
(3)取出的鞋全部成对。(4)取出的鞋至少有2只成对;(2)取出的鞋恰好有2只是成对的;(1)取出的鞋都不成对;例2.从(0,1)中随机地取两个数,求下列情况下的概率.
(1)两数之和小于1.2; (2)两数平方和小于 .方法点评:(1)设两数分别为 ,则,
(2)同样设两数分别为,则 , .∴两数之和小于1.2的点的概率 .
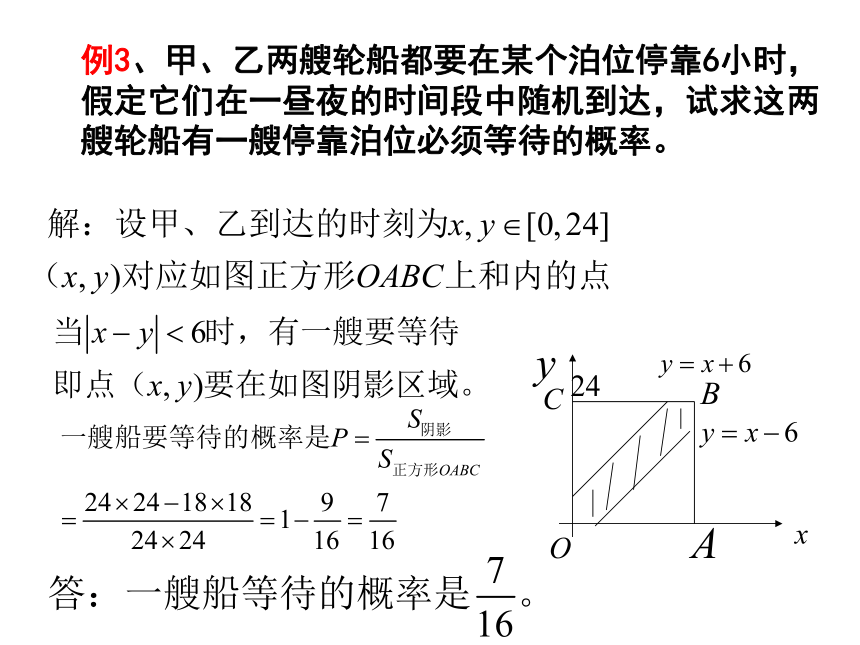
练习4、向正方形网格随机抛掷半径为1cm的硬币,已知每个小正方形的边长为5cm,求硬币与正方形的边有公共点的概率.例3、甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,试求这两艘轮船有一艘停靠泊位必须等待的概率。练习5、甲乙两人相约在8点至9点之间在某地碰头,约定早到者到达后应等20分钟方可离开.如果两人在8点至9点之间到达的时刻是随机的,求两人相遇的可能性.单元测试
选择题(每题4分,共40分)
1.下列事件中不可能事件是 ( )
A.三角形的内角和为180°
B.三角形中大边对的角大,小边对的角小
C.锐角三角形中两个内角的和小于90°
D.三角形中任意两边的和大于第三边
2.在12件同类产品中,有10件是正品,2件是次品,从中任意抽出3件的必然事件是 ( )
A.3件都是正品 B.至少有1件是次品
C.3件都是次品 D.至少有一件是正品
3.把红桃,黑桃,方块,梅花四张纸牌随机发给甲,乙,丙,丁四个人,每人分得一张,事件“甲分得梅花”与事件“乙分得梅花”是 ( )A.对立事件 B.不可能事件
C.互斥但不对立事件 D.以上答案均不对
4.掷一颗骰子,出现点数是2或4的概率是 ( )
A. B. C. D.CDCB5.将一枚质地均匀的硬币连掷4次,出现“2次正面朝上,2次反面朝上”的概率是 ( )
A . B. C. D.
6.以集合 中的任意两个元素分别作为一个分数的分子,分母,则这个分数为既约分数(分子和分母互质)的概率为( )
A. B. C. D.
7.先后抛掷两颗骰子,设出现的点数之和是12,11,10的概率依次是 ,则 ( )
A. B. C. D.
8.玻璃球盒中装有各色球12只,其中5红,4黑,2白,1绿,从中取1球为红或黑的概率为 ( )
A. B. C. D.CABD9.随机试验,同时掷三颗骰子,记录三颗骰子的点数之和,试验的基本事件总数是 ( )
A. 15 B. 16 C. 17 D.18
10.有4条线段,长度分别为1,3,5,7,从这四条线段中任取三条,则所取三条线段能构成一个三角形的概率是 ( )
A. B. C. D.BA填空题(每题4分,共16分)
11.已知 , 则 ____.
12. 将一颗骰子先后抛掷2次,出现点数之和
等于8的概率等于______________.
13.甲,乙两人下棋,甲获胜的概率为30%,两人下成和棋的概率为50%,则甲不输的概率为_____________.
14.从含有500个个体的总体中一次性地抽取25个个体,假定其中每个个体被抽到的概率相等,那么总体中的每个个体被抽取到的概率等于____________.80% 0.05求:(1)派出医生至多2人的概率;
(2)派出医生至少2人的概率.16.某医院一天内派出医生下乡医疗,派出医生人数及其概率如下:15.已知随机事件E为”掷一枚骰子,观察点数”,事件A表示”点数小于5”,事件B表示”点数是奇数”,事件C表示”点数是偶数”.问:
(1)事件A+C表示什么?
(2)事件 分别表示什么?
A+C表示出现点数为1,2,3,4,6. 0.46 0.74 17.过半径为1的圆内一条直径上任意一点作垂直于直径的弦,求弦长超过圆内接等边三角形BCD边长的概率.18.设有一正方形网格,其各个最小正方形的边长为4cm,现用直径为2cm的硬币投掷到此网格上,求硬币落下后与格线没有公共点的概率.1:判断下列给出的事件是否为互斥事件, 是否为对立事件,并说明道理.
从40张扑克牌(红桃,黑桃,方块,梅花点数从1~10各10张)中,任取一张.(1)”抽出红桃”与”抽出黑桃”;
(2)”抽出红色牌”与”抽出黑色牌”
(3)”抽出牌点数为5的倍数”与”抽出的牌点数大于9”.
思路点拨:根据互斥事件与对立事件的定义进行判断.判断是否为互斥事件,主要是看两事件是否同时发生;判断是否为对立事件,首先看是否为互斥事件,然后再看两事件是否必有一个发生,若必有一个发生,则为对立事件,否则,不是对立事件.2:在某一时期内,一条河流某处的最高水位在各个范围内的概率如下:计算在同一时期内,河流这一处的年最高水位在下列范围内的概率:
(1) ;
(2) ;
(3) .是必然事件一定互斥 D. 与与一定不互斥 【自我检测】
1.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的事件是 ( )
A.至少有1个白球和全是白球 B.至少有1个白球和至少有1个红球
C.恰有1个白球和恰有2个白球 D.至少有1个红球和全是白球
2.如果事件A,B互斥,那么 ( )
A.A+B是必然事件 B.C.3.下列命题中,真命题的个数是 ( )
①将一枚硬币抛两次,设事件A为”两次出现正面”,事件B为”只有一次出现反面”,则事件A与B是对立事件;
②若事件A与B为对立事件,则事件A与B为互斥事件
③若事件A 与B为互斥事件,则事件A与B为对立事件;
④若事件A与B为对立事件,则事件A+B为必然事件.
A.1 B. 2 C.3 D.44.甲,乙两人下棋,甲获胜的概率为40%,甲不输的概率为90%,则甲,乙两人下成和棋的概率为 ( )
A.60% B.30% C.10% D.50%
5.某射击运动员在一次射击训练中,命中10环,9环,8环,7环的概率分别为0.21,0.23,0.25,0.28.则这名运动员在一次射击中:命中10环或9环的概率是__________,少于7环的概率是____________.
6.在区间[0,10]上任取一个数,求 或 的概率___________.7.有5张1角,3张2角和2张5角的邮票,任取2张,求其中两张是同价格的概率___________.
8.已知随机事件E为”掷一枚骰子,观察点数”,事件A表示”点数小于5”,事件B表示”点数是奇数”,事件C表示”点数是偶数”.问:(1)事件A+C表示什么?(2)事件 分别表示什么?9.我国已经正式加入WTO,包括汽车在内的进口商品将最多在5年内把关税全部降低到世贸组织所要求的水平,其中有21%的进口商品恰好5年关税达到要求,18%的进口商品恰好4年关税达到要求,其余的进口商品将在3年或3年内达到要求,求进口汽车在不超过4年的时间内关税达到要求的概率.10.袋中有2个伍分硬币,2个贰分硬币,2个壹分硬币,从中任取3个,求总数超过7分的概率.
2、频率与概率的意义
3、古典概型
4、几何概型
5、互斥事件和对立事件【知识梳理】【范例点睛】
例1.有三个人,每个人都以相同的概率被分配到四个房间中的每一间.试求(1)三个人都分配到同一房间的概率;(2)至少有两个人分配到同一房间的概率.思路点拨:∵三个人以同样的概率分配到每个房间,而三个人中每个人都可以分配到四个房间中的每一间,∴共有4×4×4=64种方法.
(1)三个人分配到同一房间有4中分法,故由等可能事件的概率可知,所求的概率为.(2)设事件A为”至少有两人分配到同一房间”,则事件A的对立事件为”三个人分配到三个不同的房间”.∵三个人分配到三个不同房间共有 不同种方法,∴ ,
∴
练习1: 有两个人在一座10层大楼的底层进入电梯,设他们中的每一个人自第二层起在每一层离开是等可能的,求两人在不同层离开的概率;
2、将一枚质地均匀的硬币连续抛掷4次,求出现“2次正面朝上,2次反面朝上”的概率3、鞋柜有4双不同的鞋,随机取出4只,试求下列事件的概率:
(3)取出的鞋全部成对。(4)取出的鞋至少有2只成对;(2)取出的鞋恰好有2只是成对的;(1)取出的鞋都不成对;例2.从(0,1)中随机地取两个数,求下列情况下的概率.
(1)两数之和小于1.2; (2)两数平方和小于 .方法点评:(1)设两数分别为 ,则,
(2)同样设两数分别为,则 , .∴两数之和小于1.2的点的概率 .
练习4、向正方形网格随机抛掷半径为1cm的硬币,已知每个小正方形的边长为5cm,求硬币与正方形的边有公共点的概率.例3、甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,试求这两艘轮船有一艘停靠泊位必须等待的概率。练习5、甲乙两人相约在8点至9点之间在某地碰头,约定早到者到达后应等20分钟方可离开.如果两人在8点至9点之间到达的时刻是随机的,求两人相遇的可能性.单元测试
选择题(每题4分,共40分)
1.下列事件中不可能事件是 ( )
A.三角形的内角和为180°
B.三角形中大边对的角大,小边对的角小
C.锐角三角形中两个内角的和小于90°
D.三角形中任意两边的和大于第三边
2.在12件同类产品中,有10件是正品,2件是次品,从中任意抽出3件的必然事件是 ( )
A.3件都是正品 B.至少有1件是次品
C.3件都是次品 D.至少有一件是正品
3.把红桃,黑桃,方块,梅花四张纸牌随机发给甲,乙,丙,丁四个人,每人分得一张,事件“甲分得梅花”与事件“乙分得梅花”是 ( )A.对立事件 B.不可能事件
C.互斥但不对立事件 D.以上答案均不对
4.掷一颗骰子,出现点数是2或4的概率是 ( )
A. B. C. D.CDCB5.将一枚质地均匀的硬币连掷4次,出现“2次正面朝上,2次反面朝上”的概率是 ( )
A . B. C. D.
6.以集合 中的任意两个元素分别作为一个分数的分子,分母,则这个分数为既约分数(分子和分母互质)的概率为( )
A. B. C. D.
7.先后抛掷两颗骰子,设出现的点数之和是12,11,10的概率依次是 ,则 ( )
A. B. C. D.
8.玻璃球盒中装有各色球12只,其中5红,4黑,2白,1绿,从中取1球为红或黑的概率为 ( )
A. B. C. D.CABD9.随机试验,同时掷三颗骰子,记录三颗骰子的点数之和,试验的基本事件总数是 ( )
A. 15 B. 16 C. 17 D.18
10.有4条线段,长度分别为1,3,5,7,从这四条线段中任取三条,则所取三条线段能构成一个三角形的概率是 ( )
A. B. C. D.BA填空题(每题4分,共16分)
11.已知 , 则 ____.
12. 将一颗骰子先后抛掷2次,出现点数之和
等于8的概率等于______________.
13.甲,乙两人下棋,甲获胜的概率为30%,两人下成和棋的概率为50%,则甲不输的概率为_____________.
14.从含有500个个体的总体中一次性地抽取25个个体,假定其中每个个体被抽到的概率相等,那么总体中的每个个体被抽取到的概率等于____________.80% 0.05求:(1)派出医生至多2人的概率;
(2)派出医生至少2人的概率.16.某医院一天内派出医生下乡医疗,派出医生人数及其概率如下:15.已知随机事件E为”掷一枚骰子,观察点数”,事件A表示”点数小于5”,事件B表示”点数是奇数”,事件C表示”点数是偶数”.问:
(1)事件A+C表示什么?
(2)事件 分别表示什么?
A+C表示出现点数为1,2,3,4,6. 0.46 0.74 17.过半径为1的圆内一条直径上任意一点作垂直于直径的弦,求弦长超过圆内接等边三角形BCD边长的概率.18.设有一正方形网格,其各个最小正方形的边长为4cm,现用直径为2cm的硬币投掷到此网格上,求硬币落下后与格线没有公共点的概率.1:判断下列给出的事件是否为互斥事件, 是否为对立事件,并说明道理.
从40张扑克牌(红桃,黑桃,方块,梅花点数从1~10各10张)中,任取一张.(1)”抽出红桃”与”抽出黑桃”;
(2)”抽出红色牌”与”抽出黑色牌”
(3)”抽出牌点数为5的倍数”与”抽出的牌点数大于9”.
思路点拨:根据互斥事件与对立事件的定义进行判断.判断是否为互斥事件,主要是看两事件是否同时发生;判断是否为对立事件,首先看是否为互斥事件,然后再看两事件是否必有一个发生,若必有一个发生,则为对立事件,否则,不是对立事件.2:在某一时期内,一条河流某处的最高水位在各个范围内的概率如下:计算在同一时期内,河流这一处的年最高水位在下列范围内的概率:
(1) ;
(2) ;
(3) .是必然事件一定互斥 D. 与与一定不互斥 【自我检测】
1.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的事件是 ( )
A.至少有1个白球和全是白球 B.至少有1个白球和至少有1个红球
C.恰有1个白球和恰有2个白球 D.至少有1个红球和全是白球
2.如果事件A,B互斥,那么 ( )
A.A+B是必然事件 B.C.3.下列命题中,真命题的个数是 ( )
①将一枚硬币抛两次,设事件A为”两次出现正面”,事件B为”只有一次出现反面”,则事件A与B是对立事件;
②若事件A与B为对立事件,则事件A与B为互斥事件
③若事件A 与B为互斥事件,则事件A与B为对立事件;
④若事件A与B为对立事件,则事件A+B为必然事件.
A.1 B. 2 C.3 D.44.甲,乙两人下棋,甲获胜的概率为40%,甲不输的概率为90%,则甲,乙两人下成和棋的概率为 ( )
A.60% B.30% C.10% D.50%
5.某射击运动员在一次射击训练中,命中10环,9环,8环,7环的概率分别为0.21,0.23,0.25,0.28.则这名运动员在一次射击中:命中10环或9环的概率是__________,少于7环的概率是____________.
6.在区间[0,10]上任取一个数,求 或 的概率___________.7.有5张1角,3张2角和2张5角的邮票,任取2张,求其中两张是同价格的概率___________.
8.已知随机事件E为”掷一枚骰子,观察点数”,事件A表示”点数小于5”,事件B表示”点数是奇数”,事件C表示”点数是偶数”.问:(1)事件A+C表示什么?(2)事件 分别表示什么?9.我国已经正式加入WTO,包括汽车在内的进口商品将最多在5年内把关税全部降低到世贸组织所要求的水平,其中有21%的进口商品恰好5年关税达到要求,18%的进口商品恰好4年关税达到要求,其余的进口商品将在3年或3年内达到要求,求进口汽车在不超过4年的时间内关税达到要求的概率.10.袋中有2个伍分硬币,2个贰分硬币,2个壹分硬币,从中任取3个,求总数超过7分的概率.
