函数单调性

课件22张PPT。☆★函数的单调性 教学目标函数的单调性 地位与作用 设计反思 板书设计 重点与难点 教法与学法 教学过程 “函数的单调性”是函数重要性质之一,在
教材中起着承上启下的作用。一方面，是初中
有关内容的深化，提高，使学生对函数单调性
从感性认识提高到理性认识。另一方面，可以
通过对函数单调性的学习，为后面学习指数函
数、对数函数、及数列这种特殊的函数打下基
础，与不等式、求函数的值域、最值，导数等
等都有着紧密的联系。
地位与作用 教学目标 重点: 函数单调性的判断和应用. 重点与难点 难点: 理解函数单调性的概念,判
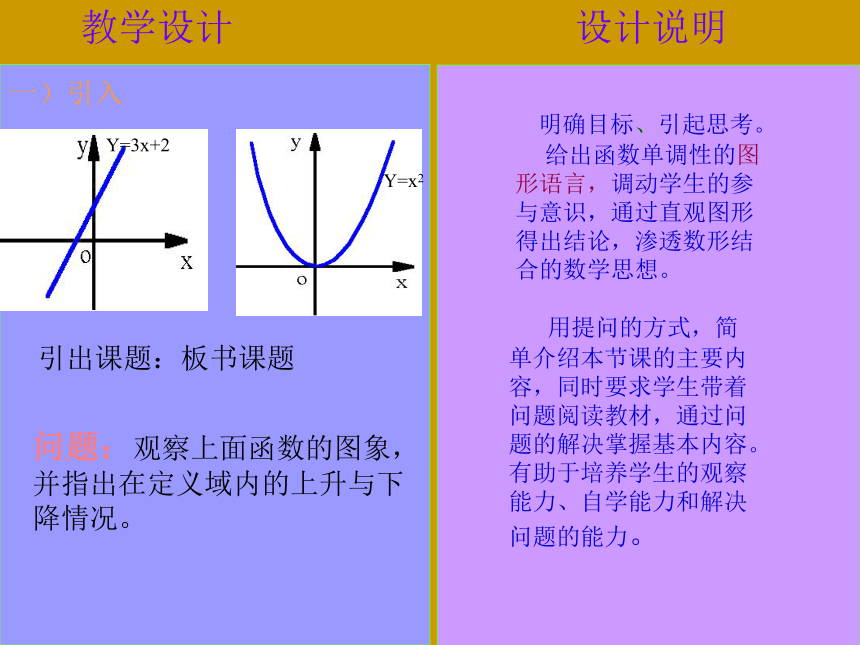
断和证明函数的单调性. 教 法: 自学辅导法，讨论法，讲授法 教法与学法 学 法: 阅读—归纳—讨论—练习 教学手段: 多媒体电脑及投影仪教学过程教学设计设计说明引出课题：板书课题一）引入问题：观察上面函数的图象，并指出在定义域内的上升与下降情况。 明确目标、引起思考。
给出函数单调性的图
形语言，调动学生的参
与意识，通过直观图形
得出结论，渗透数形结
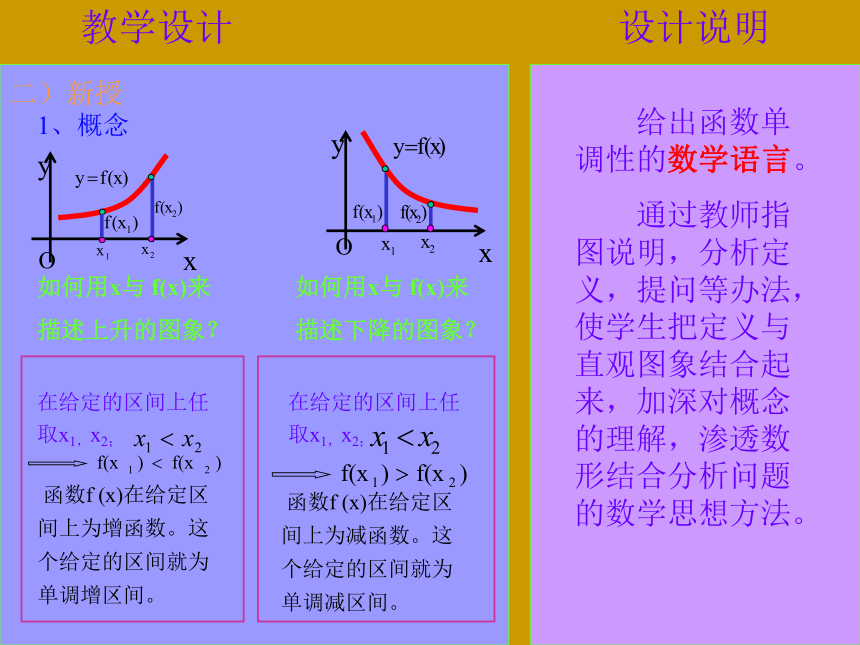
合的数学思想。 用提问的方式，简单介绍本节课的主要内容，同时要求学生带着问题阅读教材，通过问题的解决掌握基本内容。有助于培养学生的观察能力、自学能力和解决问题的能力。教学设计设计说明二）新授如何用x与 f(x)来
描述上升的图象？如何用x与 f(x)来
描述下降的图象？ 给出函数单调性的数学语言。
通过教师指图说明，分析定义，提问等办法，使学生把定义与直观图象结合起来，加深对概念的理解，渗透数形结合分析问题的数学思想方法。1、概念教学设计设计说明2、判定（证明）方法(1)图象法： 从左向右看图象的升降情况 提出问题：要求学生
结合概念中的图示及例1，
归纳总结其中的判断方法。
因例1较简单，不详细
讲解，只用多媒体演示其
图象的变化情况。
但要讲清：
①单调区间的开闭
②增、减区间的表示
③图象升、降的看法解答 通过本例培养学生的观察、分析能力。教学设计设计说明讨论一般性 通过讨论使学生深入理解和掌握概念，培养学生的抽象思维能力，培养学生研究数学的能力，学会归纳总结。教学设计设计说明(2)定义法：利用定义判定(证明)函数的增、减性例2：证明函数f(x)=3x+2在
R上是增函数。 由于例2难度较大，学生难以从中归纳出判断(证明)方法及步骤，因而有必要先详细讲解，通过分析、引导学生抽象、概括出方法及步骤，提示学生注意证明过程的规范性及严谨性。同时说明数学题型间的转化关系，使学生体验数学中的艺术美。
归纳判定(证明)方法并加以比较说明；使学生突破本节的难点，掌握重点内容。解答教学设计设计说明例3 证明函数f(x)=1/x 在
(0，+∞)上是减函数。解答教学设计设计说明 通过练习加深对概念的理解，熟悉判断方法，达到巩固，消化新知的目的。同时强化解题步骤，形成并提高解题能力。 对本节课内容
作全面小结，除知
识外，对所用到的
数学方法，也进行
适当的小结。布置选做提的目的在于分层教学.三）巩固四）作业函数的单调性板 书 设 计幻灯投影一、引入（投影）
二、新课
1、概念（投影）
2、表示方法
（1）图示法
例1： （投影）
一般性讨论（投影）
（2）定义法 例2： （投影）
步骤：（投影）
例3： （投影）
作业： （投影） 以上就是我对《函数的单调性》这节课
的教学设想.各位专家、评委，本节课我在
概念教学上进行了一些尝试.在教学过程中，
我努力创设一个探索数学的学习环境,通过设
计一系列问题,使学生在探究问题的过程中，
亲身经历数学概念的发生与发展过程，从而
逐步把握概念的实质内涵,深入理解概念. 设计反思 数与形,本是相倚依
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘,几何代数统一体
永远联系莫分离
—— 华罗庚
感谢各位老师莅临指导再 见！例1：如图是定义在闭区间[-5,5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一个单调区间上， y=f(x)是增函数还是减函数。在区间[-2,1), [3, 5]上是增函数。答：函数y=f(x)的单调区间有[-5,-2),[-2,1), [1,3), [3,5], 其中 y=f(x)在区间[-5, -2), [1,3)上是减函数，例2：证明函数f(x)=3x+2在R上是增函数。 f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)由x1即 f(x1)取值定号变形作差判断例3、证明函数f(x)=1/x 在(0，+∞)上是减函数。 证明：设x1,x2是(0，+∞)上任意两个实数，且x1 则 f(x1)- f(x2)=又由x10
所以f(x1)- f(x2)>0
即f(x1)> f(x2)
所以f(x)=1/x 在(0，+∞)上是减函数。例3、证明函数f(x)=1/x 在(0，+∞)上是减函数。法 一讨论