人教版九年级数学上册22.1.1二次函数 线上说课比赛课件(共23张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.1二次函数 线上说课比赛课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 23:49:50 | ||
图片预览







文档简介
(共25张PPT)
22.1.1二次函数
目 录
教材分析
教法学法
教学过程
学情分析
01
教材分析
一、教材分析
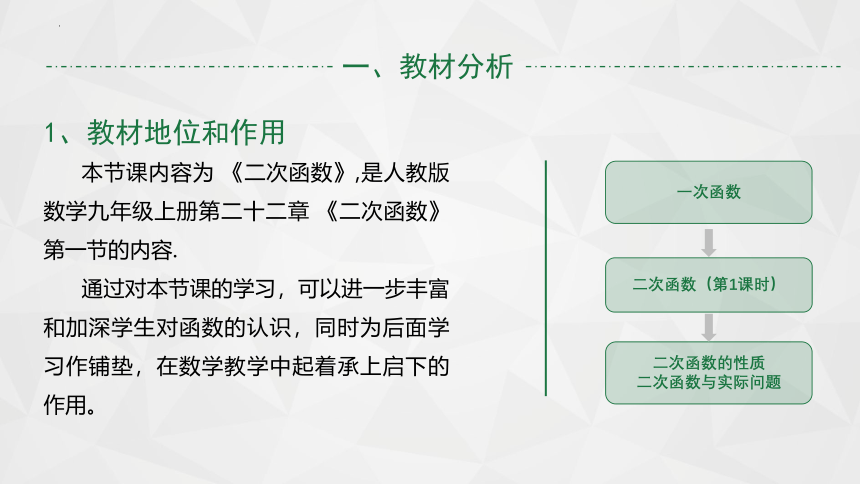
本节课内容为 《二次函数》,是人教版数学九年级上册第二十二章 《二次函数》第一节的内容.
通过对本节课的学习,可以进一步丰富和加深学生对函数的认识,同时为后面学习作铺垫,在数学教学中起着承上启下的作用。
二次函数(第1课时)
一次函数
二次函数的性质
二次函数与实际问题
1、教材地位和作用
一、教材分析
知识与技能
1.经历探索和表示二次函数关系的过程,获得二次函数的概念。
2、应用二次函数的概念解决问题。
3.通过分析实际问题的情境,确定二次函数表达式。
过程与方法
关注数学知识与实际的结合,让学生在实际背景中理解数量关系和变化规律。
经历从实际问题中建立数学模型、形成模型观念,用数学的语言表达世界。
情感与价值观
让学生在数学问题探究中,感受探索与创造,提升学习数学的兴趣,进一步发展应用意识。
2、教学的目标和要求
一、教材分析
教学重点
经历探索和表示二次函数关系的过程,获得二次函数的概念。
教学难点
通过分析实际问题的情境,确定二次函数表达式。
02
二、学情分析
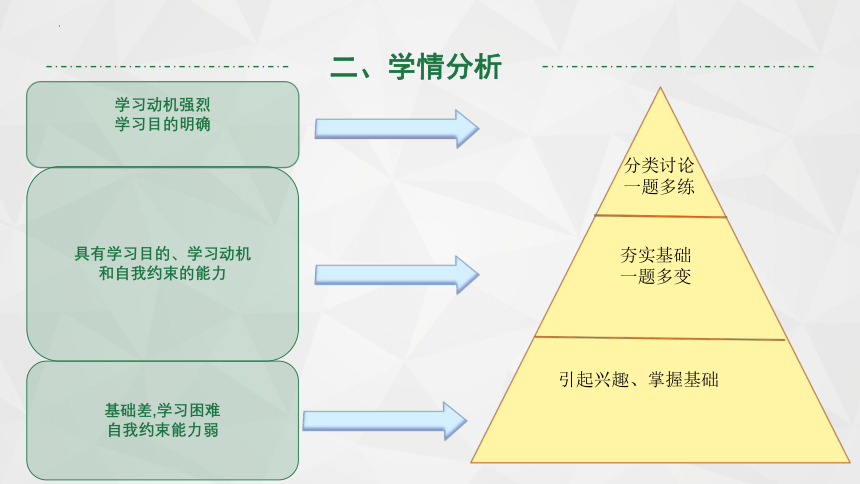
二、学情分析
学习动机强烈
学习目的明确
具有学习目的、学习动机
和自我约束的能力
基础差,学习困难
自我约束能力弱
分类讨论一题多练
夯实基础
一题多变
引起兴趣、掌握基础
03
教法学法
三、教法学法
根据学生现阶段学习情况不同,有针对的提问相应学生,促进不同层次学生积极参与课堂教学中,满足不同层次学生需要。
引导学生通过对同一题型不同形式和不同题型同一形式进行讨论研究,促进学生积极思考,独立探索,培养学生思维能力。
分层教学法
探究法
启发法
以教师为主导,通过不断设问促进学生对二次函数概念的掌握。
教法:
学法:
类比推理法、归纳法、自主学习法
04
说教学过程
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
1、如图,在靠墙(墙长为10m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为24m,
(1)求鸡场的长y(m)与宽x(m)的函数关系式,并求自变量的取值范围.
(2)求鸡场面积 S(m2)与x(m)的函数关系式,并求自变量的取值范围
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
问题1:正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,
则 y 关于x 的关系式为 .
问题2:n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
问题3:某工厂一种产品现在的年产量是20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间有什么关系?
即
即
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
这些函数有什么共同点?
注意:1. 自变量的最高次数是2。
2. 二次项的系数a≠0,可以没有一次项和常数项,但不能没有二次项。
3. 二次函数解析式必须是整式。
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
例
判断下列函数是否是二次函数
( )
( )
( )
( )
形式:
看含自变量的代数式是否为整数
化简:
将含自变量的代数式化简
判断:
根据系数、次数的要求判断
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
二次函数必须是“2”
四、说教学过程
例
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
2.如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
1、矩形窗户的周长是6m,写出窗户的面积y(m2)与窗户的宽x(m)之间的函数关系式,
根据实际问题建立函数解析式的步骤:
(1)仔细审题,设出适当的自变量;
(2)找出等量关系,列出函数解析式;
(3)根据问题的要求,作适当的变形;
(4)根据实际要求,写出自变量的取值范围(在较为复杂且没有要求的情况下,也可不必写)
四、说教学过程
4.某超市经销一种销售成本为每件20元的商品,据市场调查分析,如果按照每件25元销售,一周能售出1000件;若销售单价每涨1元,每周销售量就减少20件,设销售单价为x元(x大于25),一周销售量为y件。
(1)写出y与x的函数关系;(标明x的取值范围)
(2)设一周的销售利润为S元,写出S与x之间的函数关系式;
3.某工厂现有80台机器,每台机器平均每天生产384件产品.现准备增加一批同类机器以提高生产总量.在试生产中发现,由于其他生产条件没有改变,因此,每增加一台机器,每台机器平均每天将减少生产4件产品.如果增加x台机器,每天的生产总量为y件,请写出y与x之间的函数关系式;
例
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
实际训练法——知行统一
分层演练——注重学生间个别差异
一题多变——发散思维
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
学生方面:梳理本节课知识,系统化掌握本节课要点,同时帮助学生找到本节课的短板和不足,查漏补缺。
教师方面:在梳理总结本节课的同时,了解学生掌握情况,为后面进行教学辅导和进一步教学做准备。进行课堂小结时与教学目标进行对照,为下一步教学反思做准备。
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
作业
四、说教学过程
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
解实际问题与二次函数步骤:
22.1.1二次函数
(1)审题,设自变量;
(2)找出等量关系,
(3)列出函数解析式;
(4)写出自变量的取值范围
教学预测
能够对于实际问题建立二次函数
可能会对不同类型的当中的隐含条件会产生疑问
类型题多练寻找内在规律
在二次函数概念的获得容易实现
在实际问题建立二次函数过程中会产生审题不清、找不到隐含自变量等问题
小组内互相分析,组内探讨,类型题多练
对二次函数一般形式能够识记,实际问题解决中能够设出简单明显的自变量
列出函数关系式较难
小组合作、鼓励教学
感谢您的观看!
22.1.1二次函数
目 录
教材分析
教法学法
教学过程
学情分析
01
教材分析
一、教材分析
本节课内容为 《二次函数》,是人教版数学九年级上册第二十二章 《二次函数》第一节的内容.
通过对本节课的学习,可以进一步丰富和加深学生对函数的认识,同时为后面学习作铺垫,在数学教学中起着承上启下的作用。
二次函数(第1课时)
一次函数
二次函数的性质
二次函数与实际问题
1、教材地位和作用
一、教材分析
知识与技能
1.经历探索和表示二次函数关系的过程,获得二次函数的概念。
2、应用二次函数的概念解决问题。
3.通过分析实际问题的情境,确定二次函数表达式。
过程与方法
关注数学知识与实际的结合,让学生在实际背景中理解数量关系和变化规律。
经历从实际问题中建立数学模型、形成模型观念,用数学的语言表达世界。
情感与价值观
让学生在数学问题探究中,感受探索与创造,提升学习数学的兴趣,进一步发展应用意识。
2、教学的目标和要求
一、教材分析
教学重点
经历探索和表示二次函数关系的过程,获得二次函数的概念。
教学难点
通过分析实际问题的情境,确定二次函数表达式。
02
二、学情分析
二、学情分析
学习动机强烈
学习目的明确
具有学习目的、学习动机
和自我约束的能力
基础差,学习困难
自我约束能力弱
分类讨论一题多练
夯实基础
一题多变
引起兴趣、掌握基础
03
教法学法
三、教法学法
根据学生现阶段学习情况不同,有针对的提问相应学生,促进不同层次学生积极参与课堂教学中,满足不同层次学生需要。
引导学生通过对同一题型不同形式和不同题型同一形式进行讨论研究,促进学生积极思考,独立探索,培养学生思维能力。
分层教学法
探究法
启发法
以教师为主导,通过不断设问促进学生对二次函数概念的掌握。
教法:
学法:
类比推理法、归纳法、自主学习法
04
说教学过程
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
1、如图,在靠墙(墙长为10m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为24m,
(1)求鸡场的长y(m)与宽x(m)的函数关系式,并求自变量的取值范围.
(2)求鸡场面积 S(m2)与x(m)的函数关系式,并求自变量的取值范围
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
问题1:正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,
则 y 关于x 的关系式为 .
问题2:n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
问题3:某工厂一种产品现在的年产量是20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间有什么关系?
即
即
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
这些函数有什么共同点?
注意:1. 自变量的最高次数是2。
2. 二次项的系数a≠0,可以没有一次项和常数项,但不能没有二次项。
3. 二次函数解析式必须是整式。
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
例
判断下列函数是否是二次函数
( )
( )
( )
( )
形式:
看含自变量的代数式是否为整数
化简:
将含自变量的代数式化简
判断:
根据系数、次数的要求判断
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
二次函数必须是“2”
四、说教学过程
例
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
温故知新
讲授新课
课堂小结
布置作业
板书设计
针对训练
2.如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
1、矩形窗户的周长是6m,写出窗户的面积y(m2)与窗户的宽x(m)之间的函数关系式,
根据实际问题建立函数解析式的步骤:
(1)仔细审题,设出适当的自变量;
(2)找出等量关系,列出函数解析式;
(3)根据问题的要求,作适当的变形;
(4)根据实际要求,写出自变量的取值范围(在较为复杂且没有要求的情况下,也可不必写)
四、说教学过程
4.某超市经销一种销售成本为每件20元的商品,据市场调查分析,如果按照每件25元销售,一周能售出1000件;若销售单价每涨1元,每周销售量就减少20件,设销售单价为x元(x大于25),一周销售量为y件。
(1)写出y与x的函数关系;(标明x的取值范围)
(2)设一周的销售利润为S元,写出S与x之间的函数关系式;
3.某工厂现有80台机器,每台机器平均每天生产384件产品.现准备增加一批同类机器以提高生产总量.在试生产中发现,由于其他生产条件没有改变,因此,每增加一台机器,每台机器平均每天将减少生产4件产品.如果增加x台机器,每天的生产总量为y件,请写出y与x之间的函数关系式;
例
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
实际训练法——知行统一
分层演练——注重学生间个别差异
一题多变——发散思维
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
学生方面:梳理本节课知识,系统化掌握本节课要点,同时帮助学生找到本节课的短板和不足,查漏补缺。
教师方面:在梳理总结本节课的同时,了解学生掌握情况,为后面进行教学辅导和进一步教学做准备。进行课堂小结时与教学目标进行对照,为下一步教学反思做准备。
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
四、说教学过程
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
作业
四、说教学过程
导入新课
讲授新课
课堂小结
布置作业
板书设计
针对训练
解实际问题与二次函数步骤:
22.1.1二次函数
(1)审题,设自变量;
(2)找出等量关系,
(3)列出函数解析式;
(4)写出自变量的取值范围
教学预测
能够对于实际问题建立二次函数
可能会对不同类型的当中的隐含条件会产生疑问
类型题多练寻找内在规律
在二次函数概念的获得容易实现
在实际问题建立二次函数过程中会产生审题不清、找不到隐含自变量等问题
小组内互相分析,组内探讨,类型题多练
对二次函数一般形式能够识记,实际问题解决中能够设出简单明显的自变量
列出函数关系式较难
小组合作、鼓励教学
感谢您的观看!
同课章节目录
