高中人教A版数学1.1.1柱、锥、台、球的结构特征(一)ppt课件
文档属性
| 名称 | 高中人教A版数学1.1.1柱、锥、台、球的结构特征(一)ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 488.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-12 10:07:26 | ||
图片预览





文档简介
课件28张PPT。1.1.1柱、锥、台、球的结构特征复 习 引 入1. 经典的建筑给人以美的享受,其
中奥秘为何?世间万物,为何千姿
百态? 复 习 引 入2. 小学与初中在平面上研究过哪些
几何图形?在空间范围上研究过哪些
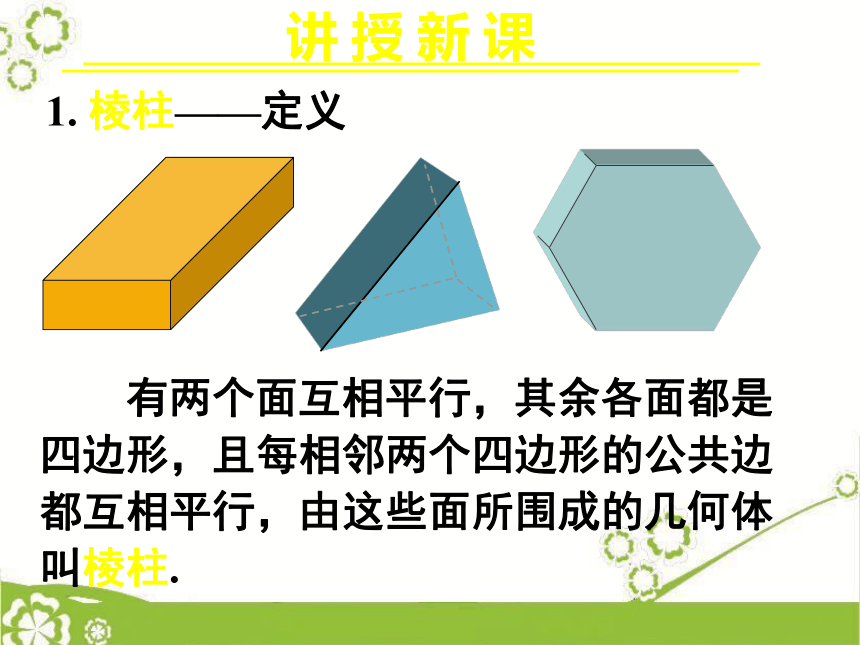
几何图形?1. 棱柱——定义讲 授 新 课 有两个面互相平行,其余各面都是
四边形,且每相邻两个四边形的公共边
都互相平行,由这些面所围成的几何体
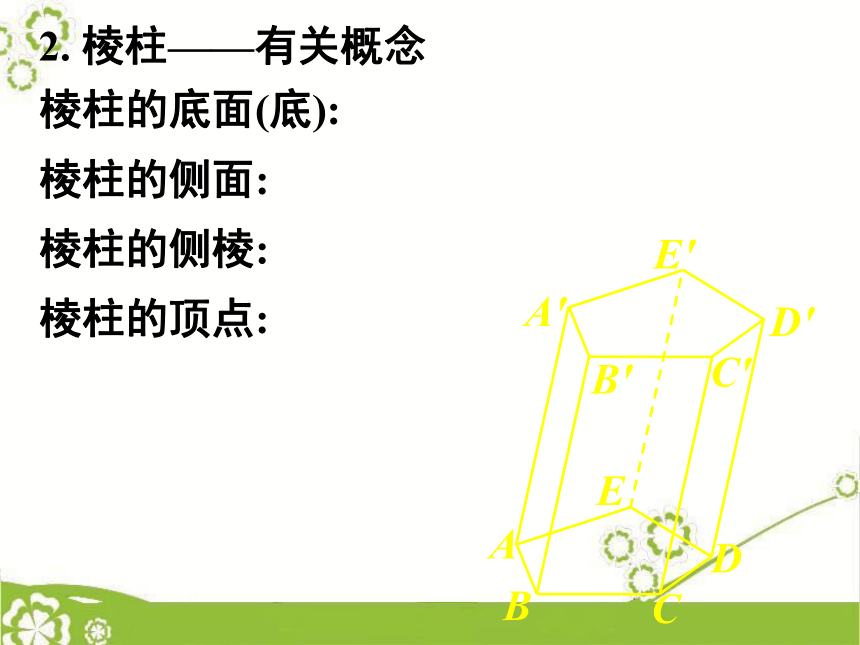
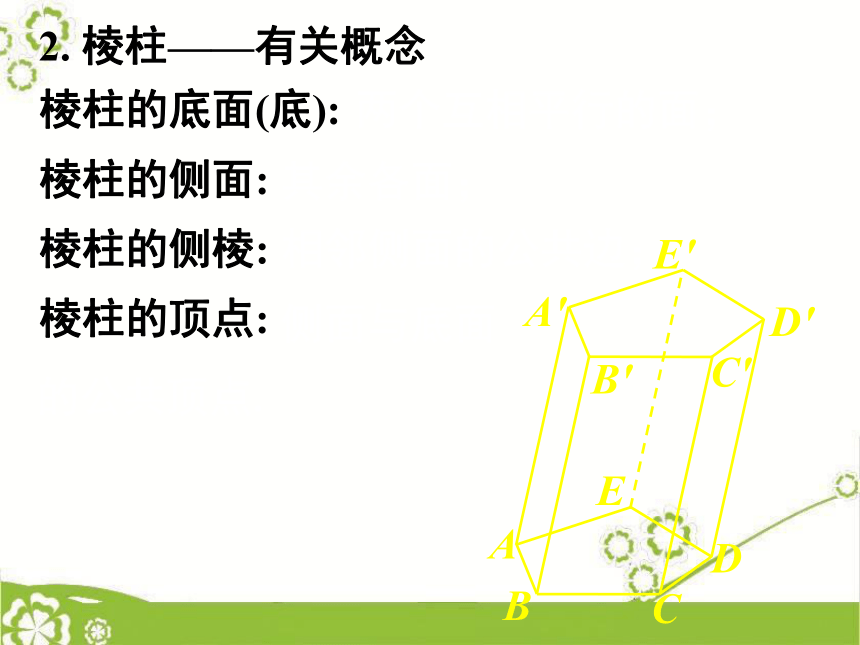
叫棱柱.讲 授 新 课1. 棱柱——定义EDACBE'D'A'C'B'棱柱的底面(底):
棱柱的侧面:
棱柱的侧棱:
棱柱的顶点:2. 棱柱——有关概念EDACBE'D'A'C'B'棱柱的底面(底):
棱柱的侧面:
棱柱的侧棱:
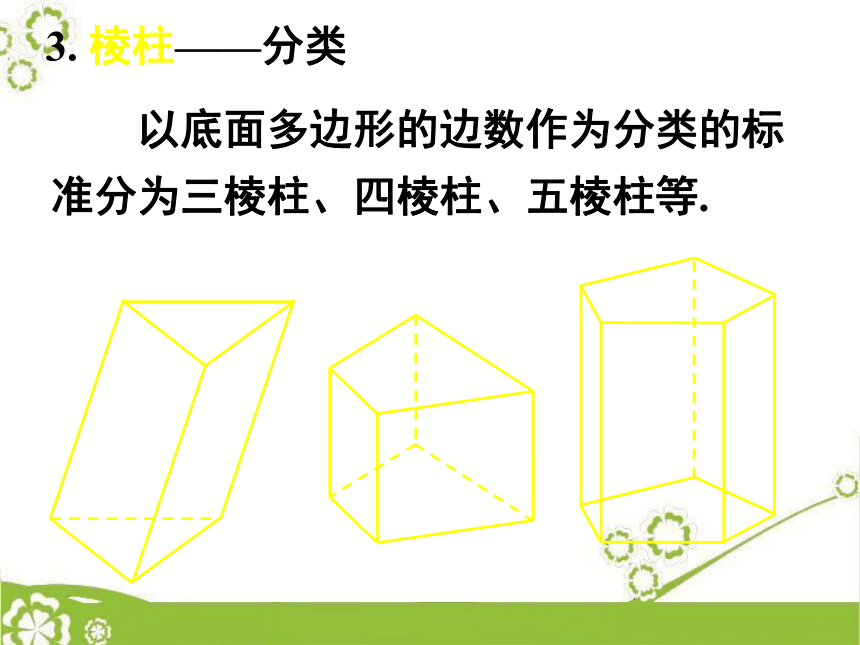
棱柱的顶点:两个互相平行的面;相邻侧面的公共边;其余各面;2. 棱柱——有关概念的公共顶点.侧面与底面 以底面多边形的边数作为分类的标
准分为三棱柱、四棱柱、五棱柱等. 3. 棱柱——分类4. 棱锥——定义 有一个面是多边形,其余各面都是
有一个公共顶点的三角形,由这些面所
围成的几何体叫棱锥.5. 棱锥——有关概念棱锥的侧面:棱锥的底面或底:棱椎的侧棱:棱锥的顶点:SBCDA5. 棱锥——有关概念棱锥的侧面:棱锥的底面或底:棱椎的侧棱:有公共顶点的各三角形;余下的那个多边形;两个相邻侧面的公共边;棱锥的顶点:各侧面的公共顶点.SBCDA棱锥的底面棱锥的侧面棱锥的顶点棱锥的侧棱BCDEAOS5. 棱锥——有关概念6. 棱锥——分类 底面是三角形、四边形、五边形
……的棱锥分别叫做三棱锥、四棱锥、
五棱锥……其中三棱锥又叫做四面体.讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?7. 圆柱、圆锥的结构特征: ① 讨论:圆柱、圆锥如何形成?7. 圆柱、圆锥的结构特征: ② 定义:
① 讨论:圆柱、圆锥如何形成?7. 圆柱、圆锥的结构特征: ② 定义:以矩形的一边所在的直线为轴
旋转,其余三边旋转所成的曲面所围成
的几何体叫圆柱;以直角三角形的一条
直角边为旋转轴,其余两边旋转所成的
曲面所围成的几何体叫圆锥.① 讨论:圆柱、圆锥如何形成? 棱柱与圆柱、棱柱与棱锥的
共同特征是什么? 讨 论:观察下面的几何体,哪些是棱柱?1. 观察下面的几何体,哪些是棱柱?练习√√√1. 观察下面的几何体,哪些是棱柱?练习2.有两个面互相平行,其余各面都是平
行四边形的几何体是不是棱柱(举反
例说明)
3.棱柱的任何两个平面都可以作为棱柱
的底面吗?练习4.教材P.7练习第1、2题. 5. 已知圆锥的轴截面等腰三角形的腰长为
5cm, 面积为12cm2,求圆锥的底面半径.
6. 已知圆柱的底面半径为3cm,轴截面面
积为24cm2,求圆柱的母线长.
7. 正四棱锥的底面积为4 cm2,侧面等
腰三角形面积为6cm2,求正四棱锥侧棱.练习 几何图形;
相关概念;
相关性质;
生活实例.课 堂 小 结课 后 作 业2. 《习案》第一课时.1. 阅读教材P.1~ P.4;
中奥秘为何?世间万物,为何千姿
百态? 复 习 引 入2. 小学与初中在平面上研究过哪些
几何图形?在空间范围上研究过哪些
几何图形?1. 棱柱——定义讲 授 新 课 有两个面互相平行,其余各面都是
四边形,且每相邻两个四边形的公共边
都互相平行,由这些面所围成的几何体
叫棱柱.讲 授 新 课1. 棱柱——定义EDACBE'D'A'C'B'棱柱的底面(底):
棱柱的侧面:
棱柱的侧棱:
棱柱的顶点:2. 棱柱——有关概念EDACBE'D'A'C'B'棱柱的底面(底):
棱柱的侧面:
棱柱的侧棱:
棱柱的顶点:两个互相平行的面;相邻侧面的公共边;其余各面;2. 棱柱——有关概念的公共顶点.侧面与底面 以底面多边形的边数作为分类的标
准分为三棱柱、四棱柱、五棱柱等. 3. 棱柱——分类4. 棱锥——定义 有一个面是多边形,其余各面都是
有一个公共顶点的三角形,由这些面所
围成的几何体叫棱锥.5. 棱锥——有关概念棱锥的侧面:棱锥的底面或底:棱椎的侧棱:棱锥的顶点:SBCDA5. 棱锥——有关概念棱锥的侧面:棱锥的底面或底:棱椎的侧棱:有公共顶点的各三角形;余下的那个多边形;两个相邻侧面的公共边;棱锥的顶点:各侧面的公共顶点.SBCDA棱锥的底面棱锥的侧面棱锥的顶点棱锥的侧棱BCDEAOS5. 棱锥——有关概念6. 棱锥——分类 底面是三角形、四边形、五边形
……的棱锥分别叫做三棱锥、四棱锥、
五棱锥……其中三棱锥又叫做四面体.讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?讨论:棱柱、棱锥分别具有一些什么几何
性质?有什么共同的性质?7. 圆柱、圆锥的结构特征: ① 讨论:圆柱、圆锥如何形成?7. 圆柱、圆锥的结构特征: ② 定义:
① 讨论:圆柱、圆锥如何形成?7. 圆柱、圆锥的结构特征: ② 定义:以矩形的一边所在的直线为轴
旋转,其余三边旋转所成的曲面所围成
的几何体叫圆柱;以直角三角形的一条
直角边为旋转轴,其余两边旋转所成的
曲面所围成的几何体叫圆锥.① 讨论:圆柱、圆锥如何形成? 棱柱与圆柱、棱柱与棱锥的
共同特征是什么? 讨 论:观察下面的几何体,哪些是棱柱?1. 观察下面的几何体,哪些是棱柱?练习√√√1. 观察下面的几何体,哪些是棱柱?练习2.有两个面互相平行,其余各面都是平
行四边形的几何体是不是棱柱(举反
例说明)
3.棱柱的任何两个平面都可以作为棱柱
的底面吗?练习4.教材P.7练习第1、2题. 5. 已知圆锥的轴截面等腰三角形的腰长为
5cm, 面积为12cm2,求圆锥的底面半径.
6. 已知圆柱的底面半径为3cm,轴截面面
积为24cm2,求圆柱的母线长.
7. 正四棱锥的底面积为4 cm2,侧面等
腰三角形面积为6cm2,求正四棱锥侧棱.练习 几何图形;
相关概念;
相关性质;
生活实例.课 堂 小 结课 后 作 业2. 《习案》第一课时.1. 阅读教材P.1~ P.4;
