沪科版八年级下册 19.1 多边形内角和课件(共33张PPT)
文档属性
| 名称 | 沪科版八年级下册 19.1 多边形内角和课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
19.1 多边形内角和
小明的设想
2018上海国际花展在上海植物园展出。清明小长假期间,小明和家人一起,慕名前去。
小明的设想
2018上海国际花展在上海植物园展出。清明小长假期间,小明和家人一起,慕名前去。
游客如梭,大家纷纷拿出相机把这些美丽的画面定格下来。
小明的设想
小明有一个设想:
要是能设计一个内角和是2018°的多边形花坛该多有意义啊!
小明的这个想法能实现吗?
19.1 多边形内角和
1、了解多边形、多边形的顶点、边、内角、外角及对角线等概念。
2、会用字母表示多边形。
3、探索并掌握求多边形内角和的方法。
4、掌握多边形内角和定理,并会应用解决问题。
学习目标
旧知回顾
※三角形内角和定理
三角形内角和为180 .
※三角形的概念
平面内,由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形,叫做三角形.
三条
探索新知
探索1. 多边形的相关概念:
⑴什么是多边形?
⑵有哪些元素?
⑶如何表示?
⑷什么是凸多边形?
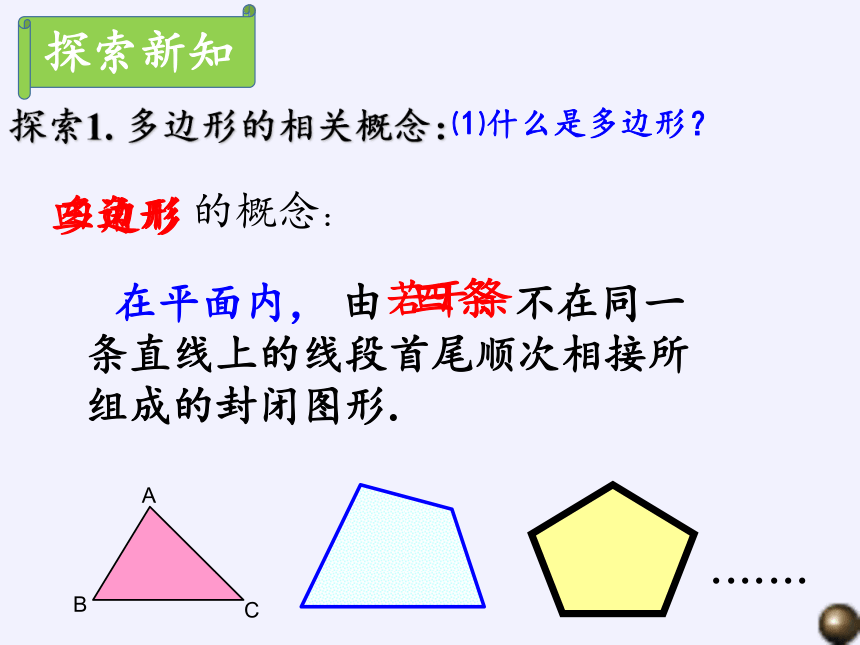
多边形
四边形
三角形
在平面内, 由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形.
的概念:
三条
A
B
C
.......
若干条
四条
探索新知
探索1. 多边形的相关概念:
⑴什么是多边形?
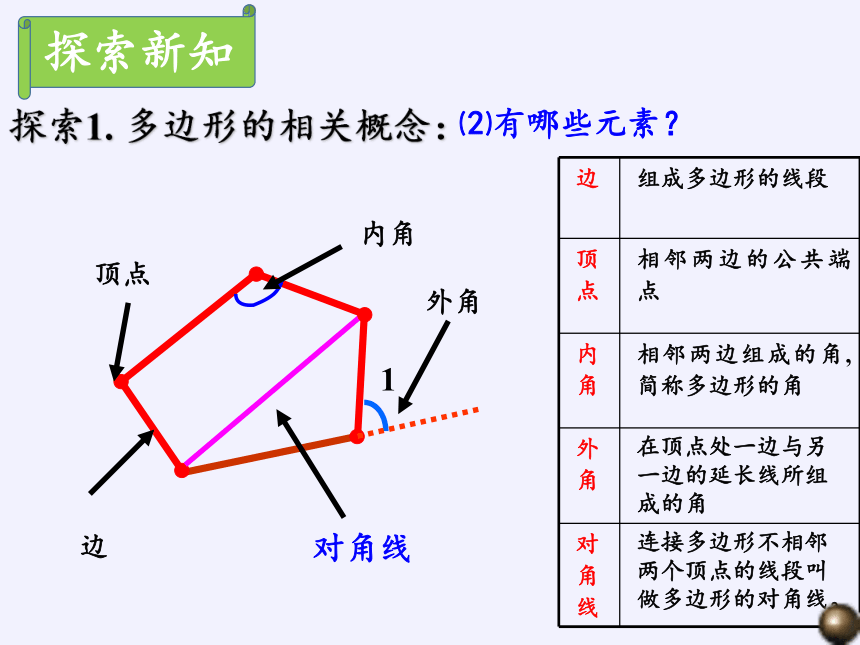
内角
对角线
外角
1
顶点
边
探索新知
边 组成多边形的线段
顶点 相邻两边的公共端点
内角 相邻两边组成的角,简称多边形的角
外角 在顶点处一边与另一边的延长线所组成的角
对角线 连接多边形不相邻两个顶点的线段叫做多边形的对角线。
⑵有哪些元素?
探索1. 多边形的相关概念:
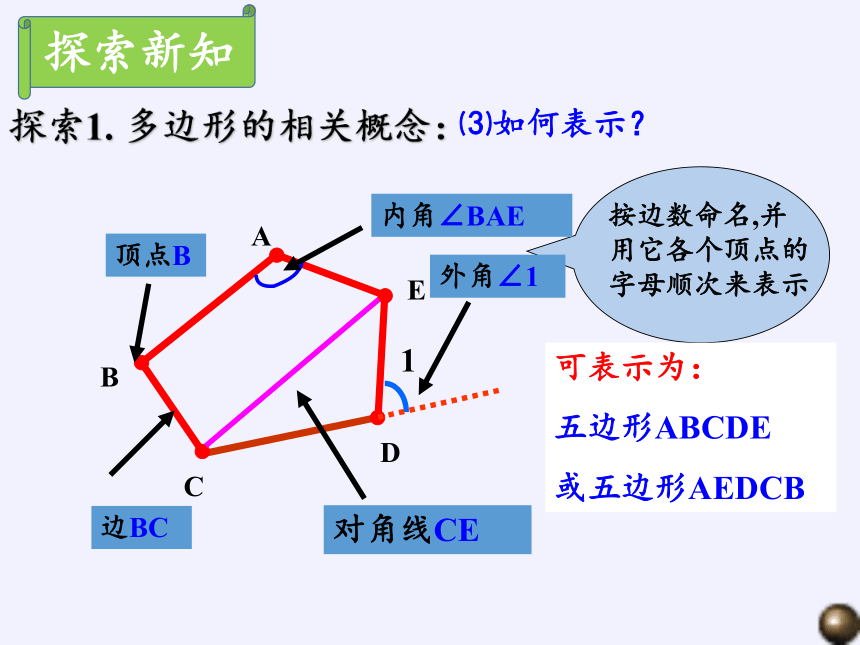
内角∠BAE
对角线CE
A
B
C
D
E
外角∠1
1
顶点B
边BC
探索新知
⑶如何表示?
可表示为:
五边形ABCDE
或五边形AEDCB
按边数命名,并用它各个顶点的字母顺次来表示
探索1. 多边形的相关概念:
凸多边形
非凸多边形
一个多边形,如果把它的任何一边双向延长,其他各边都在延长线所得直线的同一旁,这样的多边形就是凸多边形
A
B
C
D
A
B
C
D
探索新知
⑷什么是凸多边形?
注意:今后如果不作说明,我们说的多边形都是凸多边形.
探索1. 多边形的相关概念:
⑴四边形的内角和?
探索2. 多边形的内角和:
探索新知
⑵五边形的内角和?
⑶六边形的内角和?
⑷n边形的内角和?
探索新知
⑴四边形的内角和?
探索2. 多边形的内角和:
利用三角形知识探索四边形内角和等于多少度?你能想到几种办法?
想一想
1.请你试着用不同的方法得出四边形内角和,在横线上写出算式和计算结果.
2.用直尺作图,分割线用虚线表示.
动动手
探索新知
⑴四边形的内角和?
探索2. 多边形的内角和:
共同点:找一个点,将四边形转化为三角形。
共同点是什么
探索新知
⑵五边形的内角和?
探索2. 多边形的内角和:
你能仿照求四边形内角和的方法求五边形的内角和吗?
想一想
探索新知
⑶六边形的内角和?
探索2. 多边形的内角和:
你能仿照求四边形内角和的方法求六边形的内角和吗?
想一想
多边形的边数 图 形(分割成三角形) 分割出的三角形的个数 多边形的内角和
…… …… …… ……
(n-2)×180
4× 180
2× 180
3× 180
1× 180
1
2
3
4
n-2
3
4
5
6
n
探索新知
⑷n边形的内角和?
探索2. 多边形的内角和:
归纳总结
n边形的内角和等于(n-2) 180 (n≥3且为整数)
你能给出证明吗?
证明:
∵n边形有n个顶点,
∴从一个顶点出发作对角线,将n边形分割成(n-2)个三角形,
∴n边形的内角和就是这(n-2)三角形内角和之和
即 (n-2) 180
多边形内角和定理
例1:求八边形的内角和的度数。
解:当n=8时,
(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
运用新知
例2:已知,一个多边形的内角和是1800°,求它的边数。
运用新知
解 : 设这个多边形有n条边,
(n-2) ×180°=1800°
解,得 n =12
答:它的边数是12.
小明的设想
小明有一个设想:
要是能设计一个内角和是2018°的多边形花坛该多有意义啊!
小明的这个想法能实现吗?
很遗憾不能
巩固练习一:
1、七边形内角和为( )
900°
2、十七边形内角和为( )
2700°
巩固练习二:
1、多边形内角和为1260°则它是
( )边形。
2、多边形内角和为2160°则它是
( )边形。
九
十四
①
②
③
A
B
C
D
E
M
N
解:
①三角形,内角和为180°
②四边形,内角和为360°
③五边形,内角和为540°
有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
学以致用
学以致用
如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量,质检员测得∠BAE=122°,∠DCF=155°. 如果你是质检员,如何知道模板是否合格 为什么
课堂小结
1、了解多边形、多边形的顶点、边、内角、外角及对角线等概念。
2、会用字母表示多边形。
3、探索并掌握求多边形内角和的方法。
4、掌握多边形内角和定理,并会应用解决问题。
课后作业
1. 同步 19.1 (一)
从四边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从五边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从六边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
一
两
三
从n边形的一个顶点出发,可以引 __条对角线,共有 条对角线. (n≥3且为整数)
(n-3)
(1)
(2)
(3)
…
两
五
九
2. 思考
活动一:探索四边形内角和
探索研究
①过一个顶点画对角线1条,得到2个三角形,
内角和为 2×180°=3600
活动一:探索四边形内角和
探索研究
②在四边形内部任取一点,连接各顶点,
内角和为 4×180°-360°=360°
活动一:探索四边形内角和
探索研究
③在四边形一边上任取一点,连接不相邻的各顶点,
内角和为 3×180°-180°=360°
活动一:探索四边形内角和
探索研究
④在四边形外部任取一点,连接各顶点,
内角和为 3×180°-180°=360°
谢 谢
19.1 多边形内角和
小明的设想
2018上海国际花展在上海植物园展出。清明小长假期间,小明和家人一起,慕名前去。
小明的设想
2018上海国际花展在上海植物园展出。清明小长假期间,小明和家人一起,慕名前去。
游客如梭,大家纷纷拿出相机把这些美丽的画面定格下来。
小明的设想
小明有一个设想:
要是能设计一个内角和是2018°的多边形花坛该多有意义啊!
小明的这个想法能实现吗?
19.1 多边形内角和
1、了解多边形、多边形的顶点、边、内角、外角及对角线等概念。
2、会用字母表示多边形。
3、探索并掌握求多边形内角和的方法。
4、掌握多边形内角和定理,并会应用解决问题。
学习目标
旧知回顾
※三角形内角和定理
三角形内角和为180 .
※三角形的概念
平面内,由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形,叫做三角形.
三条
探索新知
探索1. 多边形的相关概念:
⑴什么是多边形?
⑵有哪些元素?
⑶如何表示?
⑷什么是凸多边形?
多边形
四边形
三角形
在平面内, 由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形.
的概念:
三条
A
B
C
.......
若干条
四条
探索新知
探索1. 多边形的相关概念:
⑴什么是多边形?
内角
对角线
外角
1
顶点
边
探索新知
边 组成多边形的线段
顶点 相邻两边的公共端点
内角 相邻两边组成的角,简称多边形的角
外角 在顶点处一边与另一边的延长线所组成的角
对角线 连接多边形不相邻两个顶点的线段叫做多边形的对角线。
⑵有哪些元素?
探索1. 多边形的相关概念:
内角∠BAE
对角线CE
A
B
C
D
E
外角∠1
1
顶点B
边BC
探索新知
⑶如何表示?
可表示为:
五边形ABCDE
或五边形AEDCB
按边数命名,并用它各个顶点的字母顺次来表示
探索1. 多边形的相关概念:
凸多边形
非凸多边形
一个多边形,如果把它的任何一边双向延长,其他各边都在延长线所得直线的同一旁,这样的多边形就是凸多边形
A
B
C
D
A
B
C
D
探索新知
⑷什么是凸多边形?
注意:今后如果不作说明,我们说的多边形都是凸多边形.
探索1. 多边形的相关概念:
⑴四边形的内角和?
探索2. 多边形的内角和:
探索新知
⑵五边形的内角和?
⑶六边形的内角和?
⑷n边形的内角和?
探索新知
⑴四边形的内角和?
探索2. 多边形的内角和:
利用三角形知识探索四边形内角和等于多少度?你能想到几种办法?
想一想
1.请你试着用不同的方法得出四边形内角和,在横线上写出算式和计算结果.
2.用直尺作图,分割线用虚线表示.
动动手
探索新知
⑴四边形的内角和?
探索2. 多边形的内角和:
共同点:找一个点,将四边形转化为三角形。
共同点是什么
探索新知
⑵五边形的内角和?
探索2. 多边形的内角和:
你能仿照求四边形内角和的方法求五边形的内角和吗?
想一想
探索新知
⑶六边形的内角和?
探索2. 多边形的内角和:
你能仿照求四边形内角和的方法求六边形的内角和吗?
想一想
多边形的边数 图 形(分割成三角形) 分割出的三角形的个数 多边形的内角和
…… …… …… ……
(n-2)×180
4× 180
2× 180
3× 180
1× 180
1
2
3
4
n-2
3
4
5
6
n
探索新知
⑷n边形的内角和?
探索2. 多边形的内角和:
归纳总结
n边形的内角和等于(n-2) 180 (n≥3且为整数)
你能给出证明吗?
证明:
∵n边形有n个顶点,
∴从一个顶点出发作对角线,将n边形分割成(n-2)个三角形,
∴n边形的内角和就是这(n-2)三角形内角和之和
即 (n-2) 180
多边形内角和定理
例1:求八边形的内角和的度数。
解:当n=8时,
(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
运用新知
例2:已知,一个多边形的内角和是1800°,求它的边数。
运用新知
解 : 设这个多边形有n条边,
(n-2) ×180°=1800°
解,得 n =12
答:它的边数是12.
小明的设想
小明有一个设想:
要是能设计一个内角和是2018°的多边形花坛该多有意义啊!
小明的这个想法能实现吗?
很遗憾不能
巩固练习一:
1、七边形内角和为( )
900°
2、十七边形内角和为( )
2700°
巩固练习二:
1、多边形内角和为1260°则它是
( )边形。
2、多边形内角和为2160°则它是
( )边形。
九
十四
①
②
③
A
B
C
D
E
M
N
解:
①三角形,内角和为180°
②四边形,内角和为360°
③五边形,内角和为540°
有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
学以致用
学以致用
如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量,质检员测得∠BAE=122°,∠DCF=155°. 如果你是质检员,如何知道模板是否合格 为什么
课堂小结
1、了解多边形、多边形的顶点、边、内角、外角及对角线等概念。
2、会用字母表示多边形。
3、探索并掌握求多边形内角和的方法。
4、掌握多边形内角和定理,并会应用解决问题。
课后作业
1. 同步 19.1 (一)
从四边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从五边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从六边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
一
两
三
从n边形的一个顶点出发,可以引 __条对角线,共有 条对角线. (n≥3且为整数)
(n-3)
(1)
(2)
(3)
…
两
五
九
2. 思考
活动一:探索四边形内角和
探索研究
①过一个顶点画对角线1条,得到2个三角形,
内角和为 2×180°=3600
活动一:探索四边形内角和
探索研究
②在四边形内部任取一点,连接各顶点,
内角和为 4×180°-360°=360°
活动一:探索四边形内角和
探索研究
③在四边形一边上任取一点,连接不相邻的各顶点,
内角和为 3×180°-180°=360°
活动一:探索四边形内角和
探索研究
④在四边形外部任取一点,连接各顶点,
内角和为 3×180°-180°=360°
谢 谢
