人教版小学数学六年级下册 第三单元 3.1 圆柱 真题同步练习(含答案)
文档属性
| 名称 | 人教版小学数学六年级下册 第三单元 3.1 圆柱 真题同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 72.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 09:45:57 | ||
图片预览



文档简介
人教版小学数学六年级下册
第三单元 3.1 圆柱 真题同步练习
一、单选题
1.(2021六下·滨海期中)如图,把底面直径6厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比原来增加30平方厘米,那么圆柱的体积是( )立方厘米。
A.30π B.45π C.60π D.180π
2.(2021六下·惠阳月考)一个圆柱的底面半径扩大到原来的3倍,高不变,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.12
3.(2021五下·岱岳期末)我们在探究圆柱体积公式时,运用的方法是( )。
A.假设 B.倒推 C.转化
4.圆柱的高和底面上的任意一条直径所成的角都是( )。
A.锐角 B.直角 C.钝角
5.(2021六下·龙华月考)有一个圆柱,底面半径是5cm,若高增加2cm,则侧面积增加( )cm2。
A.15 B.31.4 C.62.8 D.125.6
6.(2021·龙岗)一名儿童每天水的需求量约1500毫升。笑笑用里面直径8厘米、高10厘米的圆柱形水杯喝水,她一天喝( )杯水比较合适。
A.2 B.3 C.4 D.5
7.(2022六下·牡丹月考)圆柱的高不变,底面半径缩小到原来的 ,则现在圆柱的体积( )。
A.缩小到原来的 B.缩小到原来的
C.缩小到原来的 D.不变
8.(2021·坪山)已知正方体和圆柱的高相等,底面积也相等,则他们的体积( )。
A.一样大 B.正方体的体积大 C.圆柱的体积大
9.(2021·兴化)圆锥和圆柱底面积相等,体积的比是1:4,如果圆锥的高是2.4厘米,那么圆柱高是( )。
A.9.6厘米 B.3.2厘米 C.0.6厘米 D.4.2厘米
10.(2022六下·成武月考)一个圆柱的侧面展开是一个正方形,这个圆柱的底面半径和高的比是( )
A.1:π B.1:2π C.π:1 D.2:1
二、判断题
11.(2021六下·京山期中)圆柱的侧面展开可以是一个梯形。( )
12.一个圆柱的底面直径和高相等,它的侧面展开图一定是正方形。
13.(2021六下·菏泽月考)一支圆柱形铅笔长20厘米,把它截成同样长的两段后,表面积增加了30平方厘米,则原来这支铅笔的体积是300立方厘米。( )
14.(2021·承德)当圆柱的底面直径与高都是10m时,圆柱的侧面展开图一定是一个正方形。( )
15.(2021六下·惠阳月考)把一个圆柱体截成两个圆柱体之后,表面积就比原来增加了1个底面积的大小。( )
三、填空题
16.(2021六下·南华期中)一个圆锥,如果将它的底面半径和高都扩大为原来的2倍,那么它的底面积扩大到原来的 倍、体积扩大到原来的 倍。
17.(2021六下·阳东期中)一个圆柱的底面直径是8cm,高为1dm,这个圆柱的表面积是 ,体积 。
18.(2022六下·六盘水期中)一个圆柱的底面直径是4cm,高是15cm,它的侧面积是 ,表面积是 ,体积是 。
19.(2021六下·荔浦期中)把一个底面积是24dm2,高是8dm的圆柱形木材削成两个完全一样的圆锥体(如右图所示)。已知每个圆锥的底面积和圆柱的底面积相等,那么削去部分的体积是 立方分米。
20.把一根横截面半径为2分米,长4米的圆柱形木料截成同样长的5段,表面积比原来增加 平方分米。
四、解答题
21.(2021六下·淮安月考)把一个棱长8分米的正方体木块加工成一个最大的圆柱,圆柱的体积是多少立方分米?
22.(2021六下·惠阳月考)求表面积与体积。
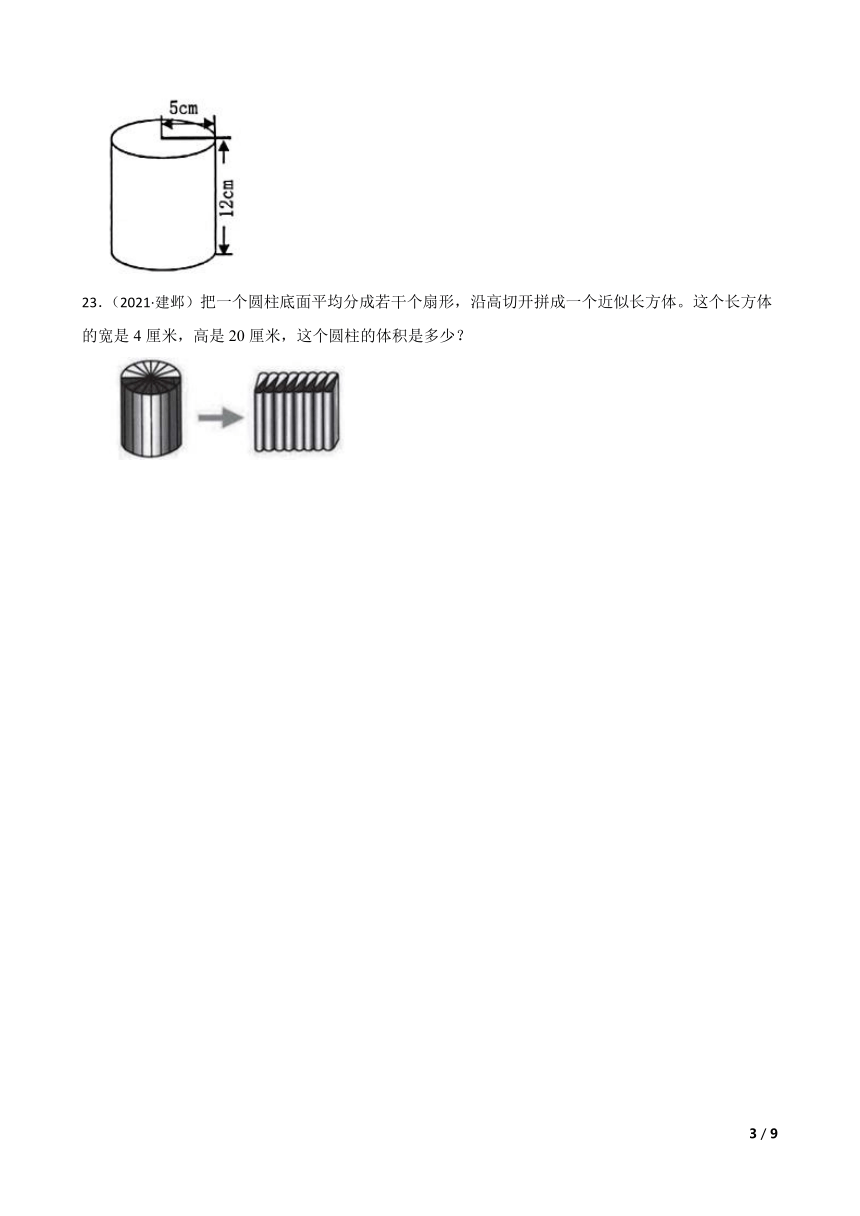
23.(2021·建邺)把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?
答案解析部分
1.【答案】B
【考点】圆柱的体积(容积)
【解析】【解答】6÷2=3(厘米)
30÷2=15(平方厘米)
15÷3=5(厘米)
3×3×π×5=45π(立方厘米)
故答案为:B。
【分析】把圆柱拼成一个近似的长方体过程中,拼成的近似长方体的体积与原圆柱体积相等,但表面积增加了两个长为圆柱高宽为圆柱底面半径的长方形。
2.【答案】C
【考点】圆柱的体积(容积)
【解析】【解答】解:3×3=9
故答案为:C。
【分析】圆柱的体积=底面积×高,其中,底面积=π×半径2,底面半径扩大到原来的3倍,高不变,它的体积扩大到原来的9倍。
3.【答案】C
【考点】圆柱的体积(容积)
【解析】【解答】解:我们在探究圆柱体积公式时,运用的方法是转化。
故答案为:C。
【分析】我们在探究圆柱体积公式时,把圆柱体分割,然后拼成一个长方体,继而推导出圆柱的体积计算公式,运用了转化的方法。
4.【答案】B
【考点】圆柱的特征
【解析】【解答】解:圆柱的高和底面上的任意一条直径所成的角都是直角。
故答案为:B。
【分析】圆柱的高是指圆柱体的上底面和下底面之间垂直高度,所以圆柱的高与底面上任意一条直径垂直,本题据此解答。
5.【答案】C
【考点】圆柱的侧面积、表面积
【解析】【解答】3.14×(5×2)×2
=3.14×10×2
=31.4×2
=62.8(cm2)
故答案为:C。
【分析】侧面积增加的面积=圆柱的底面周长×高;其中,底面周长=π×半径×2。
6.【答案】B
【考点】圆柱的体积(容积)
【解析】【解答】解:(8÷2)2×3.14×10=502.4毫升,1500÷502.4≈3杯,所以她一天喝3杯水比较合适。
故答案为:B。
【分析】圆柱形水杯的容积=(直径÷2)2×π×高,然后用儿童每天水的需求量除以圆柱形水杯的容积,然后作答即可。
7.【答案】B
【考点】圆柱的体积(容积);积的变化规律
【解析】【解答】解:圆柱的高不变,底面半径缩小到原来的 ,体积缩小到原来的 。
故答案为:B。
【分析】圆柱的体积=π×底面半径的平方×高,据此解答。
8.【答案】A
【考点】正方体的体积;圆柱的体积(容积)
【解析】【解答】解:正方体和圆柱的高相等,底面积也相等,则他们的体积一样大。
故答案为:A。
【分析】正方体的体积=圆柱的体积=底面积×高,据此作答即可。
9.【答案】A
【考点】圆柱的体积(容积);圆锥的体积(容积);比的应用
【解析】【解答】解:把圆锥和圆柱的底面积看成1平方厘米,1×2.4×=0.8平方厘米,0.8÷1×4=3.2平方厘米,3.2÷1=3.2厘米,所以圆柱的高是3.2厘米。
故答案为:B。
【分析】因为圆锥和圆柱的底面积相等,所以可以把底面积看成1平方厘米,那么圆锥的体积=底面积×高×,因为圆锥和圆柱体积的比是1:4,那么圆柱的体积=圆锥的体积÷圆锥的体积占的份数×圆柱的体积占的份数,所以圆柱的高=圆柱的体积÷底面积。
10.【答案】B
【考点】圆柱的展开图
【解析】【解答】解:设圆柱的底面半径为r,则圆柱的高=2πr,
所以圆柱的底面半径:高=r:2πr
=1:2π。
故答案为:B。
【分析】根据题意可得圆柱的底面周长等于圆柱的高,圆柱的底面周长=π×2r,进而即可得出圆柱底面半径和圆柱的高的比。
11.【答案】(1)错误
【考点】圆柱的展开图
【解析】【解答】解:圆柱的侧面展开不可能是一个梯形。
故答案为:错误。
【分析】圆柱的侧面沿高展开是一个长方形,长方形的长相当于圆柱底面周长,宽相当于圆柱的高;当底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高;斜着剪开得到一个平行四边形,平行四边形的底相当于圆柱底面周长,高相当于圆柱的高。
12.【答案】(1)错误
【考点】圆柱的展开图
【解析】【解答】 一个圆柱的底面周长和高相等,它的侧面展开图一定是正方形,原题说法错误。
故答案为:错误。
【分析】此题主要考查了圆柱的侧面展开图,将圆柱的侧面展开有很多种分法,当沿高把一个圆柱的侧面展开时,如果圆柱的底面周长和圆柱的高相等,它的侧面展开图是一个正方形;但如果不是沿高展开,它的侧面展开图就不是一个正方形,据此判断。
13.【答案】(1)正
【考点】圆柱的体积(容积)
【解析】【解答】解:30÷2×20
=15×20
=300(立方厘米)
故答案为:正确。
【分析】原来这支铅笔的体积=底面积×高;其中,底面积=增加的表面积÷2。
14.【答案】(1)错误
【考点】圆柱的侧面积、表面积
【解析】【解答】解:3.14×10=31.4(米)
31.4米>10米,圆柱的侧面展开图不是正方形。
故答案为:错误。
【分析】圆柱的侧面展开图是一个正方形时,圆柱的底面积周长和高相等,底面周长=π×直径,底面周长>高,所以不是正方形。
15.【答案】(1)错误
【考点】圆柱的侧面积、表面积
【解析】【解答】解:把一个圆柱体截成两个圆柱体之后,表面积就比原来增加了2个底面积的大小。
故答案为:错误。
【分析】把一个圆柱体截成两个圆柱体之后,多了两个横截面的面积,一个横截面的面积等于底面积,所以表面积就比原来增加了2个底面积的大小。
16.【答案】4;8
【考点】圆的面积;圆柱的体积(容积)
【解析】【解答】解:圆锥的底面积扩大到原来的22=4倍、体积扩大到原来的23=8倍。
故答案为:4;8。
【分析】圆锥的底面半径扩大到原来的几倍,那么它的底面积就扩大到原来的几2倍;
圆锥的底面积扩大a倍,高扩大b倍,那么它的体积扩大到原来的a×b倍。
17.【答案】351.68平方厘米;502.4立方厘米
【考点】圆柱的体积(容积)
【解析】【解答】解:1分米=10厘米
8÷2=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
50.24×2+3.14×8×10
=100.48+25.12×10
=100.48+251.2
=351.68(平方厘米)
50.24×10=502.4(立方厘米)
故答案为:351.68平方厘米;502.4立方厘米。
【分析】这个圆柱的表面积=底面积×2+侧面积;其中,底面积=π×半,2,半径=直径÷2,侧面积=π×直径×高;体积=底面积×高。
18.【答案】188.4cm2;213.52cm2;188.4cm3
【考点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:4×3.14×15=188.4cm2,所以侧面积是188.4cm2;(4÷2)2×3.14×2+188.4=25.12+188.4=213.52cm2,所以表面积是213.52cm2;(4÷2)2×3.14×15=188.4cm3,所以体积是188.4cm3。
故答案为:188.4cm2;213.52cm2;188.4cm3。
【分析】圆柱的侧面积=底面直径×π×高;圆柱的表面积=底面积+侧面积,其中底面积=πr2;圆柱的体积=πr2h。
19.【答案】128
【考点】圆柱的体积(容积);圆锥的体积(容积);组合体的体积的巧算
【解析】【解答】解:24×8-24×(8÷2)××2
=24×8-24×4××2
=192-96××2
=192-32×2
=192-64
=128(立方分米),
所以削去部分的体积是128立方分米。
故答案为:128。
【分析】削去部分的体积=圆柱的体积-2个圆锥的体积,圆柱的体积=圆柱的底面积×圆柱的高;圆锥的体积=圆锥的底面积×圆锥的高(圆柱的高÷2)×,代入数值计算即可得出答案。
20.【答案】100.48
【考点】圆柱的体积(容积)
【解析】【解答】解:4米=40分米
3.14×22×8
=3.14×32
=100.48(平方分米)
故答案为:100.48。
【分析】把这块木料按照这样的方法截成2段,会增加2个横截面,截成3段,会增加4个横截面;截成5段时,会增加8个横截面的面积。由此用横截面面积乘8即可求出表面积比原来增加的面积。
21.【答案】解:8÷2=4(分米)
42×3.14×8=50.24×8=401.92(立方分米)
答:圆柱的体积是401.92立方分米。
【考点】圆柱的体积(容积)
【解析】【分析】把一个正方体加工成最大的圆柱,这个圆柱的底面直径=圆柱的高=正方体的棱长,所以圆柱的底面半径=底面直径÷2,所以圆柱的体积=πr2h。
22.【答案】解:表面积:3.14×52
=3.14×25
=78.5(cm2)
78.5×2+2×5×3.14×12
=157+10×3.14×12
=157+31.4×12
=157+376.8
=533.8(cm2)
体积:78.5×12=942(cm3)
【考点】圆柱的体积(容积)
【解析】【分析】表面积=底面积×2+侧面积;其中,底面积=π×半径2,侧面积=π×半径×2×高;体积=底面积×高。
23.【答案】解:42×3.14×20
=50.24×20
=1004.8(立方厘米)
答:这个圆柱的体积是1004.8立方厘米。
【考点】圆柱的体积(容积)
【解析】【分析】从图中可以看出,长方体的宽=圆柱的底面半径,长方体的高=圆柱的高,那么这个圆柱的体积=πr2h,据此作答即可。
1 / 1
第三单元 3.1 圆柱 真题同步练习
一、单选题
1.(2021六下·滨海期中)如图,把底面直径6厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比原来增加30平方厘米,那么圆柱的体积是( )立方厘米。
A.30π B.45π C.60π D.180π
2.(2021六下·惠阳月考)一个圆柱的底面半径扩大到原来的3倍,高不变,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.12
3.(2021五下·岱岳期末)我们在探究圆柱体积公式时,运用的方法是( )。
A.假设 B.倒推 C.转化
4.圆柱的高和底面上的任意一条直径所成的角都是( )。
A.锐角 B.直角 C.钝角
5.(2021六下·龙华月考)有一个圆柱,底面半径是5cm,若高增加2cm,则侧面积增加( )cm2。
A.15 B.31.4 C.62.8 D.125.6
6.(2021·龙岗)一名儿童每天水的需求量约1500毫升。笑笑用里面直径8厘米、高10厘米的圆柱形水杯喝水,她一天喝( )杯水比较合适。
A.2 B.3 C.4 D.5
7.(2022六下·牡丹月考)圆柱的高不变,底面半径缩小到原来的 ,则现在圆柱的体积( )。
A.缩小到原来的 B.缩小到原来的
C.缩小到原来的 D.不变
8.(2021·坪山)已知正方体和圆柱的高相等,底面积也相等,则他们的体积( )。
A.一样大 B.正方体的体积大 C.圆柱的体积大
9.(2021·兴化)圆锥和圆柱底面积相等,体积的比是1:4,如果圆锥的高是2.4厘米,那么圆柱高是( )。
A.9.6厘米 B.3.2厘米 C.0.6厘米 D.4.2厘米
10.(2022六下·成武月考)一个圆柱的侧面展开是一个正方形,这个圆柱的底面半径和高的比是( )
A.1:π B.1:2π C.π:1 D.2:1
二、判断题
11.(2021六下·京山期中)圆柱的侧面展开可以是一个梯形。( )
12.一个圆柱的底面直径和高相等,它的侧面展开图一定是正方形。
13.(2021六下·菏泽月考)一支圆柱形铅笔长20厘米,把它截成同样长的两段后,表面积增加了30平方厘米,则原来这支铅笔的体积是300立方厘米。( )
14.(2021·承德)当圆柱的底面直径与高都是10m时,圆柱的侧面展开图一定是一个正方形。( )
15.(2021六下·惠阳月考)把一个圆柱体截成两个圆柱体之后,表面积就比原来增加了1个底面积的大小。( )
三、填空题
16.(2021六下·南华期中)一个圆锥,如果将它的底面半径和高都扩大为原来的2倍,那么它的底面积扩大到原来的 倍、体积扩大到原来的 倍。
17.(2021六下·阳东期中)一个圆柱的底面直径是8cm,高为1dm,这个圆柱的表面积是 ,体积 。
18.(2022六下·六盘水期中)一个圆柱的底面直径是4cm,高是15cm,它的侧面积是 ,表面积是 ,体积是 。
19.(2021六下·荔浦期中)把一个底面积是24dm2,高是8dm的圆柱形木材削成两个完全一样的圆锥体(如右图所示)。已知每个圆锥的底面积和圆柱的底面积相等,那么削去部分的体积是 立方分米。
20.把一根横截面半径为2分米,长4米的圆柱形木料截成同样长的5段,表面积比原来增加 平方分米。
四、解答题
21.(2021六下·淮安月考)把一个棱长8分米的正方体木块加工成一个最大的圆柱,圆柱的体积是多少立方分米?
22.(2021六下·惠阳月考)求表面积与体积。
23.(2021·建邺)把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?
答案解析部分
1.【答案】B
【考点】圆柱的体积(容积)
【解析】【解答】6÷2=3(厘米)
30÷2=15(平方厘米)
15÷3=5(厘米)
3×3×π×5=45π(立方厘米)
故答案为:B。
【分析】把圆柱拼成一个近似的长方体过程中,拼成的近似长方体的体积与原圆柱体积相等,但表面积增加了两个长为圆柱高宽为圆柱底面半径的长方形。
2.【答案】C
【考点】圆柱的体积(容积)
【解析】【解答】解:3×3=9
故答案为:C。
【分析】圆柱的体积=底面积×高,其中,底面积=π×半径2,底面半径扩大到原来的3倍,高不变,它的体积扩大到原来的9倍。
3.【答案】C
【考点】圆柱的体积(容积)
【解析】【解答】解:我们在探究圆柱体积公式时,运用的方法是转化。
故答案为:C。
【分析】我们在探究圆柱体积公式时,把圆柱体分割,然后拼成一个长方体,继而推导出圆柱的体积计算公式,运用了转化的方法。
4.【答案】B
【考点】圆柱的特征
【解析】【解答】解:圆柱的高和底面上的任意一条直径所成的角都是直角。
故答案为:B。
【分析】圆柱的高是指圆柱体的上底面和下底面之间垂直高度,所以圆柱的高与底面上任意一条直径垂直,本题据此解答。
5.【答案】C
【考点】圆柱的侧面积、表面积
【解析】【解答】3.14×(5×2)×2
=3.14×10×2
=31.4×2
=62.8(cm2)
故答案为:C。
【分析】侧面积增加的面积=圆柱的底面周长×高;其中,底面周长=π×半径×2。
6.【答案】B
【考点】圆柱的体积(容积)
【解析】【解答】解:(8÷2)2×3.14×10=502.4毫升,1500÷502.4≈3杯,所以她一天喝3杯水比较合适。
故答案为:B。
【分析】圆柱形水杯的容积=(直径÷2)2×π×高,然后用儿童每天水的需求量除以圆柱形水杯的容积,然后作答即可。
7.【答案】B
【考点】圆柱的体积(容积);积的变化规律
【解析】【解答】解:圆柱的高不变,底面半径缩小到原来的 ,体积缩小到原来的 。
故答案为:B。
【分析】圆柱的体积=π×底面半径的平方×高,据此解答。
8.【答案】A
【考点】正方体的体积;圆柱的体积(容积)
【解析】【解答】解:正方体和圆柱的高相等,底面积也相等,则他们的体积一样大。
故答案为:A。
【分析】正方体的体积=圆柱的体积=底面积×高,据此作答即可。
9.【答案】A
【考点】圆柱的体积(容积);圆锥的体积(容积);比的应用
【解析】【解答】解:把圆锥和圆柱的底面积看成1平方厘米,1×2.4×=0.8平方厘米,0.8÷1×4=3.2平方厘米,3.2÷1=3.2厘米,所以圆柱的高是3.2厘米。
故答案为:B。
【分析】因为圆锥和圆柱的底面积相等,所以可以把底面积看成1平方厘米,那么圆锥的体积=底面积×高×,因为圆锥和圆柱体积的比是1:4,那么圆柱的体积=圆锥的体积÷圆锥的体积占的份数×圆柱的体积占的份数,所以圆柱的高=圆柱的体积÷底面积。
10.【答案】B
【考点】圆柱的展开图
【解析】【解答】解:设圆柱的底面半径为r,则圆柱的高=2πr,
所以圆柱的底面半径:高=r:2πr
=1:2π。
故答案为:B。
【分析】根据题意可得圆柱的底面周长等于圆柱的高,圆柱的底面周长=π×2r,进而即可得出圆柱底面半径和圆柱的高的比。
11.【答案】(1)错误
【考点】圆柱的展开图
【解析】【解答】解:圆柱的侧面展开不可能是一个梯形。
故答案为:错误。
【分析】圆柱的侧面沿高展开是一个长方形,长方形的长相当于圆柱底面周长,宽相当于圆柱的高;当底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高;斜着剪开得到一个平行四边形,平行四边形的底相当于圆柱底面周长,高相当于圆柱的高。
12.【答案】(1)错误
【考点】圆柱的展开图
【解析】【解答】 一个圆柱的底面周长和高相等,它的侧面展开图一定是正方形,原题说法错误。
故答案为:错误。
【分析】此题主要考查了圆柱的侧面展开图,将圆柱的侧面展开有很多种分法,当沿高把一个圆柱的侧面展开时,如果圆柱的底面周长和圆柱的高相等,它的侧面展开图是一个正方形;但如果不是沿高展开,它的侧面展开图就不是一个正方形,据此判断。
13.【答案】(1)正
【考点】圆柱的体积(容积)
【解析】【解答】解:30÷2×20
=15×20
=300(立方厘米)
故答案为:正确。
【分析】原来这支铅笔的体积=底面积×高;其中,底面积=增加的表面积÷2。
14.【答案】(1)错误
【考点】圆柱的侧面积、表面积
【解析】【解答】解:3.14×10=31.4(米)
31.4米>10米,圆柱的侧面展开图不是正方形。
故答案为:错误。
【分析】圆柱的侧面展开图是一个正方形时,圆柱的底面积周长和高相等,底面周长=π×直径,底面周长>高,所以不是正方形。
15.【答案】(1)错误
【考点】圆柱的侧面积、表面积
【解析】【解答】解:把一个圆柱体截成两个圆柱体之后,表面积就比原来增加了2个底面积的大小。
故答案为:错误。
【分析】把一个圆柱体截成两个圆柱体之后,多了两个横截面的面积,一个横截面的面积等于底面积,所以表面积就比原来增加了2个底面积的大小。
16.【答案】4;8
【考点】圆的面积;圆柱的体积(容积)
【解析】【解答】解:圆锥的底面积扩大到原来的22=4倍、体积扩大到原来的23=8倍。
故答案为:4;8。
【分析】圆锥的底面半径扩大到原来的几倍,那么它的底面积就扩大到原来的几2倍;
圆锥的底面积扩大a倍,高扩大b倍,那么它的体积扩大到原来的a×b倍。
17.【答案】351.68平方厘米;502.4立方厘米
【考点】圆柱的体积(容积)
【解析】【解答】解:1分米=10厘米
8÷2=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
50.24×2+3.14×8×10
=100.48+25.12×10
=100.48+251.2
=351.68(平方厘米)
50.24×10=502.4(立方厘米)
故答案为:351.68平方厘米;502.4立方厘米。
【分析】这个圆柱的表面积=底面积×2+侧面积;其中,底面积=π×半,2,半径=直径÷2,侧面积=π×直径×高;体积=底面积×高。
18.【答案】188.4cm2;213.52cm2;188.4cm3
【考点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:4×3.14×15=188.4cm2,所以侧面积是188.4cm2;(4÷2)2×3.14×2+188.4=25.12+188.4=213.52cm2,所以表面积是213.52cm2;(4÷2)2×3.14×15=188.4cm3,所以体积是188.4cm3。
故答案为:188.4cm2;213.52cm2;188.4cm3。
【分析】圆柱的侧面积=底面直径×π×高;圆柱的表面积=底面积+侧面积,其中底面积=πr2;圆柱的体积=πr2h。
19.【答案】128
【考点】圆柱的体积(容积);圆锥的体积(容积);组合体的体积的巧算
【解析】【解答】解:24×8-24×(8÷2)××2
=24×8-24×4××2
=192-96××2
=192-32×2
=192-64
=128(立方分米),
所以削去部分的体积是128立方分米。
故答案为:128。
【分析】削去部分的体积=圆柱的体积-2个圆锥的体积,圆柱的体积=圆柱的底面积×圆柱的高;圆锥的体积=圆锥的底面积×圆锥的高(圆柱的高÷2)×,代入数值计算即可得出答案。
20.【答案】100.48
【考点】圆柱的体积(容积)
【解析】【解答】解:4米=40分米
3.14×22×8
=3.14×32
=100.48(平方分米)
故答案为:100.48。
【分析】把这块木料按照这样的方法截成2段,会增加2个横截面,截成3段,会增加4个横截面;截成5段时,会增加8个横截面的面积。由此用横截面面积乘8即可求出表面积比原来增加的面积。
21.【答案】解:8÷2=4(分米)
42×3.14×8=50.24×8=401.92(立方分米)
答:圆柱的体积是401.92立方分米。
【考点】圆柱的体积(容积)
【解析】【分析】把一个正方体加工成最大的圆柱,这个圆柱的底面直径=圆柱的高=正方体的棱长,所以圆柱的底面半径=底面直径÷2,所以圆柱的体积=πr2h。
22.【答案】解:表面积:3.14×52
=3.14×25
=78.5(cm2)
78.5×2+2×5×3.14×12
=157+10×3.14×12
=157+31.4×12
=157+376.8
=533.8(cm2)
体积:78.5×12=942(cm3)
【考点】圆柱的体积(容积)
【解析】【分析】表面积=底面积×2+侧面积;其中,底面积=π×半径2,侧面积=π×半径×2×高;体积=底面积×高。
23.【答案】解:42×3.14×20
=50.24×20
=1004.8(立方厘米)
答:这个圆柱的体积是1004.8立方厘米。
【考点】圆柱的体积(容积)
【解析】【分析】从图中可以看出,长方体的宽=圆柱的底面半径,长方体的高=圆柱的高,那么这个圆柱的体积=πr2h,据此作答即可。
1 / 1
