2021-2022学年下学期上海市小学数学五年级期末典型试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年下学期上海市小学数学五年级期末典型试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 134.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览




文档简介
2021-2022学年下学期上海市小学数学五年级期末典型试卷2
一.选择题(共12小题)
1.一个长26厘米,宽19厘米,高7毫米的长方体物体,最有可能是( )
A.橡皮 B.冰箱 C.数学书 D.普通手机
2.下面关于长方体和正方体的关系描述正确的是( )
A.长方体和正方体没有关系
B.正方体是特殊的长方体
C.长方体是特殊的正方体
3.一个数是9的倍数,这个数一定是( )的倍数.
A.3 B.2 C.5 D.6
4.在四位数12□□中的方框里填上数字,使它能同时被2、3、5整除,最多有( )种填法.
A.2 B.3 C.4 D.5
5.互质的两个数( )
A.都是质数
B.都是合数
C.可能是质数也可能是合数
6.一个长方体水池,从里面量长、宽、高都是1米,水池的( )是1立方米.
A.体积 B.容积 C.重量 D.面积
7.一个正方体的棱长之和是24厘米,它的体积是( )
A.8厘米3 B.24厘米3 C.16厘米3 D.64厘米3
8.把的分子加上12,要使分数的大小不变,分母应( )
A.加上12 B.乘4 C.除以4 D.加32
9.下面的约分正确的是( )
A. B. C.
10.下列分数中不能化成有限小数的是( )
A. B. C. D.
11.下列图形中,( )的对称轴最多.
A.正方形 B.等边三角形 C.等腰梯形 D.圆形
12.有15个零件,其中一个是质量较轻的次品,如果用天平称,至少要称( )次才能找到这个次品.
A.2 B.3 C.4 D.5
二.填空题(共6小题)
13.如果15÷3=5,我们就说15是3的 , 是15的因数.
14.一个四位数543□是3的倍数,□里可以填 ;若这个数既是2的倍数又是3的倍数,□里可以填 ;若这个数同时是2、3、5的倍数,□里填 .
15.在连续的自然数中,两个都是质数的是 和 .
16.挖一个长4米,宽3米,深3米的长方体水池,这个水池占地 平方米.
17.4个是 ;是 个.
18.要观察病人的体温,用 统计图表示比较合适.
三.判断题(共3小题)
19.一个数的最大因数是6,这个数的因数有4个. (判断对错)
20.两个不同的质数一定是互质数. .(判断对错)
21.合数都能被2整除. .
四.计算题(共2小题)
22.计算:
23.计算:21
五.应用题(共2小题)
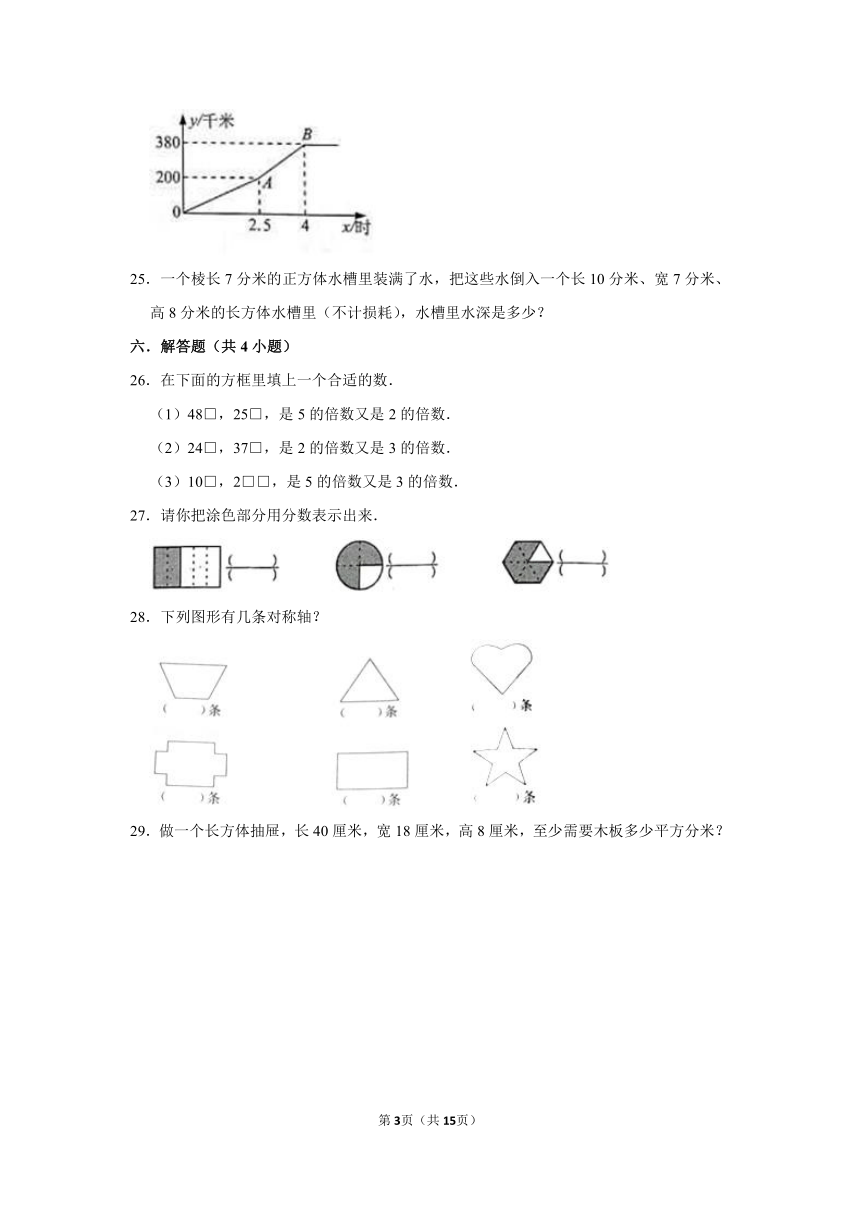
24.国庆节期间,王老师一家自驾游去了离家380千米的某地,右面是他们离家的距离y(千米)与汽车行驶时间x(时)之间的关系图.
(1)他们出发30分钟时,离家多少千米?
(2)他们出发3小时时,离目的地还有多少千米?
25.一个棱长7分米的正方体水槽里装满了水,把这些水倒入一个长10分米、宽7分米、高8分米的长方体水槽里(不计损耗),水槽里水深是多少?
六.解答题(共4小题)
26.在下面的方框里填上一个合适的数.
(1)48□,25□,是5的倍数又是2的倍数.
(2)24□,37□,是2的倍数又是3的倍数.
(3)10□,2□□,是5的倍数又是3的倍数.
27.请你把涂色部分用分数表示出来.
28.下列图形有几条对称轴?
29.做一个长方体抽屉,长40厘米,宽18厘米,高8厘米,至少需要木板多少平方分米?
2021-2022学年上海市人教新版五年级下学期期末典型试卷汇编2
参考答案与试题解析
一.选择题(共12小题)
1.一个长26厘米,宽19厘米,高7毫米的长方体物体,最有可能是( )
A.橡皮 B.冰箱 C.数学书 D.普通手机
【分析】根据生活实际,一本数学书,长约26厘米,宽约19厘米,厚度约7毫米,
橡皮的尺寸要远远小于这些数据,冰箱的尺寸要远远大于这些数据,
根据生活实际,普通手机的尺寸大约是长15厘米,宽7厘米、高0.6厘米;
由此推测可能是数学书.
【解答】解:一个长26厘米,宽19厘米,高7毫米的长方体物体,最有可能是数学书,
故选:C.
【点评】解答此题的关键是结合生活实际,明白1厘米实际有多长.
2.下面关于长方体和正方体的关系描述正确的是( )
A.长方体和正方体没有关系
B.正方体是特殊的长方体
C.长方体是特殊的正方体
【分析】根据题意,对各选项进行依次分析、进而得出结论.
【解答】解:根据分析可知:长方体和正方体没有关系,说法错误,正方体是特殊的长方体,是六个面都相等的长方体;
故选:B.
【点评】本题主要考查了长方体、正方体的特征、体积表面积的计算以及它们之间的关系.
3.一个数是9的倍数,这个数一定是( )的倍数.
A.3 B.2 C.5 D.6
【分析】因为9是3倍数,所以一个数是9的倍数,这个数一定是3的倍数.据此判断.
【解答】解:因为9是3倍数,所以一个数是9的倍数,这个数一定是3的倍数.
故选:A.
【点评】此题考查的目的是理解倍数的意义,掌握求一个数的倍数的方法.
4.在四位数12□□中的方框里填上数字,使它能同时被2、3、5整除,最多有( )种填法.
A.2 B.3 C.4 D.5
【分析】根据2、3、5倍数的特征可知;个位上必需是0,才能满足既是2的倍数又是5的倍数,现在四位数变成12□0;然后再判断是不是3的倍数即可,3的倍数的特征是:各个数位上的和是3的倍数这个数就是3的倍数,把12□0中1、2、0加起来,即1+2+0=3,分析3再加上几是3的倍数,□里就填几,然后数出填法有几种即可.
【解答】解:12□0中1、2、0加起来,即1+2+0=3,
3+0=3,
3+3=6,
3+6=9,
3+9=12,
所以在□里可以填0、3、6、9,共有4种填法;
故选:C.
【点评】本题主要考查2、3、5倍数的特征,重点考查3的倍数特征:各个数位上的和是3的倍数这个数就是3的倍数.
5.互质的两个数( )
A.都是质数
B.都是合数
C.可能是质数也可能是合数
【分析】根据质数的因数只有1和它本身,可得两个不同的质数的公因数只有1,所以它们一定是互质数;互质的两个数可能是一个质数、一个合数,例如:3和4;据此选择.
【解答】解:互质的两个数可能是一个质数、一个合数,例如:3和4,所以互质的两个数可能是质数也可能是合数.
故选:C.
【点评】此题主要考查了质数、合数、互质数的特征和应用,要熟练掌握.
6.一个长方体水池,从里面量长、宽、高都是1米,水池的( )是1立方米.
A.体积 B.容积 C.重量 D.面积
【分析】求这个水池可蓄水多少立方米,是求长方体水池的容积,根据体积的计算方法,长方体的体积=长×宽×高来计算.
【解答】解:因为长方体水池,从里面量长、宽、高都是1米,
所以水池的容积是1×1×1=1立方米.
故水池的容积是1立方米.
故选:B.
【点评】此题考查长方体的容积,解决此题的关键是分清体积和容积的区别.
7.一个正方体的棱长之和是24厘米,它的体积是( )
A.8厘米3 B.24厘米3 C.16厘米3 D.64厘米3
【分析】已知正方体的棱长总和,要求正方体的体积,先求出正方体的棱长,用正方体的棱长总和÷12=正方体的棱长,然后用公式:正方体的体积=棱长×棱长×棱长,据此列式解答.
【解答】解:正方体的棱长:24÷12=2(厘米);
正方体的体积:
2×2×2
=4×2
=8(立方厘米)
答:它的体积是8立方厘米.
故选:A.
【点评】解决本题关键是根据正方体的棱长=棱长和÷12,求出正方体的棱长,再根据正方体的体积公式求解.
8.把的分子加上12,要使分数的大小不变,分母应( )
A.加上12 B.乘4 C.除以4 D.加32
【分析】根据分数的基本性质,分数的分子 和分母同时乘或除以相同的数,分数的大小不变.把的分子加上12,也就是分子扩大5倍,要使分数的大小不变,分母也扩大5倍,据此解答即可.
【解答】解:原分数分子是3,现在分数的分子是3+12=15,扩大5倍,
原分数分母是8,要使前后分数相等,分母也应扩大5倍,变为40,即40=8+32;
答:分母应加32.
故选:D.
【点评】此题主要利用分数的基本性质解答问题,先观察分子或分母之间的变化,发现规律,再进一步通过计算解答问题.
9.下面的约分正确的是( )
A. B. C.
【分析】约分:将分子和分母数共同的约数约去(也就是除以那个数)剩下如果还有相同因数就继续约去,直到公约数为1为止,据此判断即可.
【解答】解:因为是最简分数,
所以A不正确;
因为,
所以B不正确;
因为,
所以C正确.
故选:C.
【点评】此题主要考查了约分的方法,要熟练掌握.
10.下列分数中不能化成有限小数的是( )
A. B. C. D.
【分析】首先,要看分数是否是最简分数,不是的,先把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.据此逐项分析后再选择.
【解答】解:A、是最简分数,分母中只含有质因数2,能化成有限小数;
B、是最简分数,分母中只含有质因数2,能化成有限小数;
C、是最简分数,分母中含有质因数2和3,不能化成有限小数;
D、是最简分数,分母中只含有质因数5和2,能化成有限小数.
故选:C.
【点评】此题主要考查什么样的分数可以化成有限小数,根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
11.下列图形中,( )的对称轴最多.
A.正方形 B.等边三角形 C.等腰梯形 D.圆形
【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,从而可以作出正确选择.
【解答】解:(1)因为正方形沿两组对边的中线及其对角线对折,对折后的两部分都能完全重合,则正方形是轴对称图形,
两组对边的中线及其对角线就是其对称轴,所以正方形有4条对称轴;
(2)因为等边三角形分别沿三条边的中线所在的直线对折,对折后的两部分都能完全重合,
则等边三角形是轴对称图形,三条边的中线所在的直线就是对称轴,
所以等边三角形有3条对称轴;
(3)因为等腰梯形沿上底与下底的中点的连线对折,对折后的两部分都能完全重合,则等腰梯形是轴对称图形,
上底与下底的中点的连线就是其对称轴,所以等腰梯形有1条对称轴;
(4)因为圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,则圆是轴对称图形,
任意一条直径所在的直线就是圆的对称轴,
所以说圆有无数条对称轴.
所以说圆的对称轴最多.
故选:D.
【点评】解答此题的主要依据是:轴对称图形的概念及特征.
12.有15个零件,其中一个是质量较轻的次品,如果用天平称,至少要称( )次才能找到这个次品.
A.2 B.3 C.4 D.5
【分析】第一次:把15个零件平均分成3份,每份5个,分别放在天平秤两端,若天平秤平衡,则较轻的即在未取的5个中(按照下面方法操作),若天平秤不平衡;第二次:从天平秤较高端的5个零件中任取4个,平均分成两份,每份2个,分别放在天平秤两端,若天平秤平衡,则未取那个即为较轻的,若天平秤不平衡;第三次:把天平秤较高端的2个分别放在天平秤两端,较高端的即为较轻的,据此即可解答.
【解答】解:第一次:把15个零件平均分成3份,每份5个,分别放在天平秤两端,若天平秤平衡,则较轻的即在未取的5个中(按照下面方法操作),若天平秤不平衡;
第二次:从天平秤较高端的5个零件中任取4个,平均分成两份,每份2个,分别放在天平秤两端,若天平秤平衡,则未取那个即为较轻的,若天平秤不平衡;
第三次:把天平秤较高端的2个分别放在天平秤两端,较高端的即为较轻的.
故选:B.
【点评】本题考查总数的:正确运用天平秤平衡原理解决问题.
二.填空题(共6小题)
13.如果15÷3=5,我们就说15是3的 倍数 , 3 是15的因数.
【分析】根据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;进行解答即可.
【解答】解:15÷3=5,我们就说15是3的倍数,3是15的因数.
故答案为:倍数,3.
【点评】此题应根据因数和倍数的意义进行分析、解答.
14.一个四位数543□是3的倍数,□里可以填 0、3、6、9 ;若这个数既是2的倍数又是3的倍数,□里可以填 0、6 ;若这个数同时是2、3、5的倍数,□里填 0 .
【分析】结合题意,并根据3的倍数的特征:即该数各个数位上数的和能被3整除;进行解答即可;
既是2的倍数,又是3的倍数的数需满足:个位上是0、2、4、6、8,而且各个数位上的数的和是3的倍数;
根据2,3,5倍数的特征可知:要使四位数543□同时能被2、3、5整除,个位上必需是0,才可以满足同时是2和5的倍数,然后把其它数位上的数加起来5+4+3=12,正好是3的倍数,据此解答.
【解答】解:根据分析可知:一个四位数543□是3的倍数,□里可以填:0、3、6、9;
这个数既是2的倍数又是3的倍数,□里可以填:0、6;
这个数同时是2、3、5的倍数,□里填:0.
故答案为:0、3、6、9,0、6,0.
【点评】本题主要考查能被2、3、5整数的数的特征,注意牢固掌握能被2、3、5整除的数的特征.注意基础知识的灵活运用.
15.在连续的自然数中,两个都是质数的是 2 和 3 .
【分析】根据质数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.在连续的自然数中,两个都是质数的只有2和3.
【解答】解:在连续的自然数中,两个都是质数的只有2和3.
故答案为:2、3.
【点评】此题考查的目的是理解掌握质数的概念及意义.明确:在自然数中,相邻两个自然数都是质数的只有2和3.
16.挖一个长4米,宽3米,深3米的长方体水池,这个水池占地 12 平方米.
【分析】由题意可知:求水池的占地面积,实际上是求上口的面积,水池的长和宽已知,利用长方形的面积公式即可求解.
【解答】解:4×3=12(平方米)
答:这个水池占地12平方米.
故答案为:12.
【点评】解答此题的关键是明白:求水池的占地面积,实际上是求上口的面积.
17.4个是 ;是 3 个.
【分析】根据分数的意义,有几个分数单位就是几分之几.
【解答】解:4个是 ;是 3个.
故答案为:,3.
【点评】本题考查了分数的意义和分数单位的意义,关键是找清楚有几个分数单位.
18.要观察病人的体温,用 折线 统计图表示比较合适.
【分析】折线统计图能明确看出病人的提问升降程度,便于观察,据此填空.
【解答】解:要观察病人的体温,用折线统计图表示比较合适.
故答案为:折线.
【点评】此题考查统计图的选择,根据实际情况,选择最能明显观察出问题的统计图.
三.判断题(共3小题)
19.一个数的最大因数是6,这个数的因数有4个. √ (判断对错)
【分析】首先根据:一个数的最大因数是6,可得:这个数是6;然后根据找一个数的因数,可以一对一对的找,把写成两个数的乘积,那么每一个乘积中的因数都是的因数,判断出这个数的因数有多少个即可.
【解答】解:因为一个数的最大因数是6,
所以这个数是6,
所以这个数的因数有4个:1、2、3、6,
所以题中说法正确.
故答案为:√.
【点评】此题主要考查了找一个数的因数的方法,要熟练掌握,解答此题的关键是要明确:一个数最大的因数是它本身.
20.两个不同的质数一定是互质数. √ .(判断对错)
【分析】质数只有1和它本身两个因数,互质数是两个数的公因数只有1,由此解答即可.
【解答】解:因为质数只有1和它本身两个因数,所以两个不同的质数一定是互质数;
故答案为:√.
【点评】解答此题主要是根据质数和互质数的意义进行判断.
21.合数都能被2整除. × .
【分析】合数的意义是:一个自然数如果除了1和它本身还有别的因数,这样的数叫做合数;能被2整除的数叫做偶数,能被2整除的数的特征是:个位上是0,2,4,6,8的数;由此解答.
【解答】解:合数都能被2整除这种说法是错误的.如,9、15、21等这些数是合数但是它们都不能被2整除.
故答案为:×.
【点评】此题的解答主要明确合数的意义,和能被2整除的数的特征.
四.计算题(共2小题)
22.计算:
【分析】按照从左向右的顺序进行计算。
【解答】解:
=2
=2
【点评】只含有一级运算的,按照从左向右的顺序进行计算。
23.计算:21
【分析】从左向右进行计算即可。
【解答】解:21
=21
=1
【点评】此题考查了分数的四则混合运算,注意运算顺序和运算法则。
五.应用题(共2小题)
24.国庆节期间,王老师一家自驾游去了离家380千米的某地,右面是他们离家的距离y(千米)与汽车行驶时间x(时)之间的关系图.
(1)他们出发30分钟时,离家多少千米?
(2)他们出发3小时时,离目的地还有多少千米?
【分析】(1)把30分钟化成0.5小时,2.5小时行驶了200千米,用200除以2.5求出速度,用速度乘0.5小时就是他们出发30分钟时,离家多少千米.
(2)观察图发现,2.5小时前后的速度不相同,用380千米减去200千米求出从2.5小时到4小时这段时间走的路程,然后再除以(4﹣2.5)小时求出这段时间的速度,再用这段时间的速度乘(3﹣2.5)小时求出(3﹣2.5)小时行驶的路程,再用380千米分别减去200千米和(3﹣2.5)小时行驶的路程就是离目的地还有多少千米.
【解答】解:(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米.
(2)(380﹣200)÷(4﹣2.5)×(3﹣2.5)
=180÷1.5×0.5
=60(千米)
380﹣200﹣60
=180﹣60
=120(千米)
答:离目的地还有120千米.
【点评】本题考查了速度、时间与路程关系式的应用,关键是根据2.5小时行驶了200千米求出速度.要注意2.5小时前后的速度不相同.
25.一个棱长7分米的正方体水槽里装满了水,把这些水倒入一个长10分米、宽7分米、高8分米的长方体水槽里(不计损耗),水槽里水深是多少?
【分析】利用正方体的体积计算公式,可以先求出正方体水槽内水的体积,把水全部倒进长方体的水槽里,水的体积没有变,因此用水的体积除以长方体的底面积解答即可。
【解答】解:(7×7×7)÷(10×7)
=343÷70
=4.9(分米)
答:水槽里水深是4.9分米。
【点评】此题属于应用长方体和正方体的体积计算公式解决实际问题,考查的目的是理解掌握长方体、正方体的体积计算及解决问题的能力。
六.解答题(共4小题)
26.在下面的方框里填上一个合适的数.
(1)48□,25□,是5的倍数又是2的倍数.
(2)24□,37□,是2的倍数又是3的倍数.
(3)10□,2□□,是5的倍数又是3的倍数.
【分析】(1)既是2的倍数又是5的倍数的数的特征是个位上是0,由此解答;
(2)是2的倍数又是3的倍数的数的特征是个位是偶数,且各位数字和是3的整数倍,或者这个数一定是2和3的最小公倍数6的整数倍,由此得解.
(3)是5的倍数又是3的倍数的数个位上要首先满足是5或0,然后分析是不是3的倍数.
【解答】解:(1)根据题意分析可得,既是2的倍数又是5的倍数的数的特征是个位上是0,即480,250.方框里填0,0.
答:方框里填写0,0符合题意,即480,250.
(2)由是2的倍数又是3的倍数的数的特征是个位是偶数,且各位数字和是3的整数倍,或者这个数一定是2和3的最小公倍数6的整数倍可得,240,372或378,由此可得.
答:方框里填写0,2或者8合适,即240,372或378.
(3)是5的倍数又是3的倍数的数个位上要满足是5或0,并且各位数字之和是3的倍数.分析可得105,225,255或者285.
答:方框里填写5,25(或者55,或者85).即105,225(或者255,或者285).
【点评】本题主要考查了是2,3,5的倍数的数字的特征,要熟练理解掌握.
27.请你把涂色部分用分数表示出来.
【分析】(1)把一个长方形的面积看作单位“1”,把它平均分成5份,每份是它的,其中2份涂色,表示.
(2)把一个圆的面积看作单位“1”,把它平均分成4份,每份是它的,其中3份涂色,表示.
(3)把一个正六边形的面积看作单位“1”,把它平均分成6份,每份是它的,其中5份涂色,表示.
【解答】解:把涂色部分用分数表示出来.
【点评】此题是考查分数的意义.把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数.
28.下列图形有几条对称轴?
【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此可以数出它们的对称轴.
【解答】解:
故答案为:1,1,1,2,2,5.
【点评】解答此题的主要依据是:轴对称图形的意义及其特征.注意画对称轴要用虚线.
29.做一个长方体抽屉,长40厘米,宽18厘米,高8厘米,至少需要木板多少平方分米?
【分析】首先要明确长方体木抽屉共有5个面,即四周的侧面加上一个底面就是本题要求的问题,注意单位名称的统一.
【解答】解:(40×8+18×8)×2+40×18
=(320+144)×2+720
=928+720
=1648(平方厘米),
1648平方厘米=16.48平方分米;
答;至少需要木板16.48平方分米.
【点评】把四周的面积加上一个底面积就是做一个这样抽屉需要的木板的面积
第1页(共1页)
一.选择题(共12小题)
1.一个长26厘米,宽19厘米,高7毫米的长方体物体,最有可能是( )
A.橡皮 B.冰箱 C.数学书 D.普通手机
2.下面关于长方体和正方体的关系描述正确的是( )
A.长方体和正方体没有关系
B.正方体是特殊的长方体
C.长方体是特殊的正方体
3.一个数是9的倍数,这个数一定是( )的倍数.
A.3 B.2 C.5 D.6
4.在四位数12□□中的方框里填上数字,使它能同时被2、3、5整除,最多有( )种填法.
A.2 B.3 C.4 D.5
5.互质的两个数( )
A.都是质数
B.都是合数
C.可能是质数也可能是合数
6.一个长方体水池,从里面量长、宽、高都是1米,水池的( )是1立方米.
A.体积 B.容积 C.重量 D.面积
7.一个正方体的棱长之和是24厘米,它的体积是( )
A.8厘米3 B.24厘米3 C.16厘米3 D.64厘米3
8.把的分子加上12,要使分数的大小不变,分母应( )
A.加上12 B.乘4 C.除以4 D.加32
9.下面的约分正确的是( )
A. B. C.
10.下列分数中不能化成有限小数的是( )
A. B. C. D.
11.下列图形中,( )的对称轴最多.
A.正方形 B.等边三角形 C.等腰梯形 D.圆形
12.有15个零件,其中一个是质量较轻的次品,如果用天平称,至少要称( )次才能找到这个次品.
A.2 B.3 C.4 D.5
二.填空题(共6小题)
13.如果15÷3=5,我们就说15是3的 , 是15的因数.
14.一个四位数543□是3的倍数,□里可以填 ;若这个数既是2的倍数又是3的倍数,□里可以填 ;若这个数同时是2、3、5的倍数,□里填 .
15.在连续的自然数中,两个都是质数的是 和 .
16.挖一个长4米,宽3米,深3米的长方体水池,这个水池占地 平方米.
17.4个是 ;是 个.
18.要观察病人的体温,用 统计图表示比较合适.
三.判断题(共3小题)
19.一个数的最大因数是6,这个数的因数有4个. (判断对错)
20.两个不同的质数一定是互质数. .(判断对错)
21.合数都能被2整除. .
四.计算题(共2小题)
22.计算:
23.计算:21
五.应用题(共2小题)
24.国庆节期间,王老师一家自驾游去了离家380千米的某地,右面是他们离家的距离y(千米)与汽车行驶时间x(时)之间的关系图.
(1)他们出发30分钟时,离家多少千米?
(2)他们出发3小时时,离目的地还有多少千米?
25.一个棱长7分米的正方体水槽里装满了水,把这些水倒入一个长10分米、宽7分米、高8分米的长方体水槽里(不计损耗),水槽里水深是多少?
六.解答题(共4小题)
26.在下面的方框里填上一个合适的数.
(1)48□,25□,是5的倍数又是2的倍数.
(2)24□,37□,是2的倍数又是3的倍数.
(3)10□,2□□,是5的倍数又是3的倍数.
27.请你把涂色部分用分数表示出来.
28.下列图形有几条对称轴?
29.做一个长方体抽屉,长40厘米,宽18厘米,高8厘米,至少需要木板多少平方分米?
2021-2022学年上海市人教新版五年级下学期期末典型试卷汇编2
参考答案与试题解析
一.选择题(共12小题)
1.一个长26厘米,宽19厘米,高7毫米的长方体物体,最有可能是( )
A.橡皮 B.冰箱 C.数学书 D.普通手机
【分析】根据生活实际,一本数学书,长约26厘米,宽约19厘米,厚度约7毫米,
橡皮的尺寸要远远小于这些数据,冰箱的尺寸要远远大于这些数据,
根据生活实际,普通手机的尺寸大约是长15厘米,宽7厘米、高0.6厘米;
由此推测可能是数学书.
【解答】解:一个长26厘米,宽19厘米,高7毫米的长方体物体,最有可能是数学书,
故选:C.
【点评】解答此题的关键是结合生活实际,明白1厘米实际有多长.
2.下面关于长方体和正方体的关系描述正确的是( )
A.长方体和正方体没有关系
B.正方体是特殊的长方体
C.长方体是特殊的正方体
【分析】根据题意,对各选项进行依次分析、进而得出结论.
【解答】解:根据分析可知:长方体和正方体没有关系,说法错误,正方体是特殊的长方体,是六个面都相等的长方体;
故选:B.
【点评】本题主要考查了长方体、正方体的特征、体积表面积的计算以及它们之间的关系.
3.一个数是9的倍数,这个数一定是( )的倍数.
A.3 B.2 C.5 D.6
【分析】因为9是3倍数,所以一个数是9的倍数,这个数一定是3的倍数.据此判断.
【解答】解:因为9是3倍数,所以一个数是9的倍数,这个数一定是3的倍数.
故选:A.
【点评】此题考查的目的是理解倍数的意义,掌握求一个数的倍数的方法.
4.在四位数12□□中的方框里填上数字,使它能同时被2、3、5整除,最多有( )种填法.
A.2 B.3 C.4 D.5
【分析】根据2、3、5倍数的特征可知;个位上必需是0,才能满足既是2的倍数又是5的倍数,现在四位数变成12□0;然后再判断是不是3的倍数即可,3的倍数的特征是:各个数位上的和是3的倍数这个数就是3的倍数,把12□0中1、2、0加起来,即1+2+0=3,分析3再加上几是3的倍数,□里就填几,然后数出填法有几种即可.
【解答】解:12□0中1、2、0加起来,即1+2+0=3,
3+0=3,
3+3=6,
3+6=9,
3+9=12,
所以在□里可以填0、3、6、9,共有4种填法;
故选:C.
【点评】本题主要考查2、3、5倍数的特征,重点考查3的倍数特征:各个数位上的和是3的倍数这个数就是3的倍数.
5.互质的两个数( )
A.都是质数
B.都是合数
C.可能是质数也可能是合数
【分析】根据质数的因数只有1和它本身,可得两个不同的质数的公因数只有1,所以它们一定是互质数;互质的两个数可能是一个质数、一个合数,例如:3和4;据此选择.
【解答】解:互质的两个数可能是一个质数、一个合数,例如:3和4,所以互质的两个数可能是质数也可能是合数.
故选:C.
【点评】此题主要考查了质数、合数、互质数的特征和应用,要熟练掌握.
6.一个长方体水池,从里面量长、宽、高都是1米,水池的( )是1立方米.
A.体积 B.容积 C.重量 D.面积
【分析】求这个水池可蓄水多少立方米,是求长方体水池的容积,根据体积的计算方法,长方体的体积=长×宽×高来计算.
【解答】解:因为长方体水池,从里面量长、宽、高都是1米,
所以水池的容积是1×1×1=1立方米.
故水池的容积是1立方米.
故选:B.
【点评】此题考查长方体的容积,解决此题的关键是分清体积和容积的区别.
7.一个正方体的棱长之和是24厘米,它的体积是( )
A.8厘米3 B.24厘米3 C.16厘米3 D.64厘米3
【分析】已知正方体的棱长总和,要求正方体的体积,先求出正方体的棱长,用正方体的棱长总和÷12=正方体的棱长,然后用公式:正方体的体积=棱长×棱长×棱长,据此列式解答.
【解答】解:正方体的棱长:24÷12=2(厘米);
正方体的体积:
2×2×2
=4×2
=8(立方厘米)
答:它的体积是8立方厘米.
故选:A.
【点评】解决本题关键是根据正方体的棱长=棱长和÷12,求出正方体的棱长,再根据正方体的体积公式求解.
8.把的分子加上12,要使分数的大小不变,分母应( )
A.加上12 B.乘4 C.除以4 D.加32
【分析】根据分数的基本性质,分数的分子 和分母同时乘或除以相同的数,分数的大小不变.把的分子加上12,也就是分子扩大5倍,要使分数的大小不变,分母也扩大5倍,据此解答即可.
【解答】解:原分数分子是3,现在分数的分子是3+12=15,扩大5倍,
原分数分母是8,要使前后分数相等,分母也应扩大5倍,变为40,即40=8+32;
答:分母应加32.
故选:D.
【点评】此题主要利用分数的基本性质解答问题,先观察分子或分母之间的变化,发现规律,再进一步通过计算解答问题.
9.下面的约分正确的是( )
A. B. C.
【分析】约分:将分子和分母数共同的约数约去(也就是除以那个数)剩下如果还有相同因数就继续约去,直到公约数为1为止,据此判断即可.
【解答】解:因为是最简分数,
所以A不正确;
因为,
所以B不正确;
因为,
所以C正确.
故选:C.
【点评】此题主要考查了约分的方法,要熟练掌握.
10.下列分数中不能化成有限小数的是( )
A. B. C. D.
【分析】首先,要看分数是否是最简分数,不是的,先把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.据此逐项分析后再选择.
【解答】解:A、是最简分数,分母中只含有质因数2,能化成有限小数;
B、是最简分数,分母中只含有质因数2,能化成有限小数;
C、是最简分数,分母中含有质因数2和3,不能化成有限小数;
D、是最简分数,分母中只含有质因数5和2,能化成有限小数.
故选:C.
【点评】此题主要考查什么样的分数可以化成有限小数,根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
11.下列图形中,( )的对称轴最多.
A.正方形 B.等边三角形 C.等腰梯形 D.圆形
【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,从而可以作出正确选择.
【解答】解:(1)因为正方形沿两组对边的中线及其对角线对折,对折后的两部分都能完全重合,则正方形是轴对称图形,
两组对边的中线及其对角线就是其对称轴,所以正方形有4条对称轴;
(2)因为等边三角形分别沿三条边的中线所在的直线对折,对折后的两部分都能完全重合,
则等边三角形是轴对称图形,三条边的中线所在的直线就是对称轴,
所以等边三角形有3条对称轴;
(3)因为等腰梯形沿上底与下底的中点的连线对折,对折后的两部分都能完全重合,则等腰梯形是轴对称图形,
上底与下底的中点的连线就是其对称轴,所以等腰梯形有1条对称轴;
(4)因为圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,则圆是轴对称图形,
任意一条直径所在的直线就是圆的对称轴,
所以说圆有无数条对称轴.
所以说圆的对称轴最多.
故选:D.
【点评】解答此题的主要依据是:轴对称图形的概念及特征.
12.有15个零件,其中一个是质量较轻的次品,如果用天平称,至少要称( )次才能找到这个次品.
A.2 B.3 C.4 D.5
【分析】第一次:把15个零件平均分成3份,每份5个,分别放在天平秤两端,若天平秤平衡,则较轻的即在未取的5个中(按照下面方法操作),若天平秤不平衡;第二次:从天平秤较高端的5个零件中任取4个,平均分成两份,每份2个,分别放在天平秤两端,若天平秤平衡,则未取那个即为较轻的,若天平秤不平衡;第三次:把天平秤较高端的2个分别放在天平秤两端,较高端的即为较轻的,据此即可解答.
【解答】解:第一次:把15个零件平均分成3份,每份5个,分别放在天平秤两端,若天平秤平衡,则较轻的即在未取的5个中(按照下面方法操作),若天平秤不平衡;
第二次:从天平秤较高端的5个零件中任取4个,平均分成两份,每份2个,分别放在天平秤两端,若天平秤平衡,则未取那个即为较轻的,若天平秤不平衡;
第三次:把天平秤较高端的2个分别放在天平秤两端,较高端的即为较轻的.
故选:B.
【点评】本题考查总数的:正确运用天平秤平衡原理解决问题.
二.填空题(共6小题)
13.如果15÷3=5,我们就说15是3的 倍数 , 3 是15的因数.
【分析】根据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;进行解答即可.
【解答】解:15÷3=5,我们就说15是3的倍数,3是15的因数.
故答案为:倍数,3.
【点评】此题应根据因数和倍数的意义进行分析、解答.
14.一个四位数543□是3的倍数,□里可以填 0、3、6、9 ;若这个数既是2的倍数又是3的倍数,□里可以填 0、6 ;若这个数同时是2、3、5的倍数,□里填 0 .
【分析】结合题意,并根据3的倍数的特征:即该数各个数位上数的和能被3整除;进行解答即可;
既是2的倍数,又是3的倍数的数需满足:个位上是0、2、4、6、8,而且各个数位上的数的和是3的倍数;
根据2,3,5倍数的特征可知:要使四位数543□同时能被2、3、5整除,个位上必需是0,才可以满足同时是2和5的倍数,然后把其它数位上的数加起来5+4+3=12,正好是3的倍数,据此解答.
【解答】解:根据分析可知:一个四位数543□是3的倍数,□里可以填:0、3、6、9;
这个数既是2的倍数又是3的倍数,□里可以填:0、6;
这个数同时是2、3、5的倍数,□里填:0.
故答案为:0、3、6、9,0、6,0.
【点评】本题主要考查能被2、3、5整数的数的特征,注意牢固掌握能被2、3、5整除的数的特征.注意基础知识的灵活运用.
15.在连续的自然数中,两个都是质数的是 2 和 3 .
【分析】根据质数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.在连续的自然数中,两个都是质数的只有2和3.
【解答】解:在连续的自然数中,两个都是质数的只有2和3.
故答案为:2、3.
【点评】此题考查的目的是理解掌握质数的概念及意义.明确:在自然数中,相邻两个自然数都是质数的只有2和3.
16.挖一个长4米,宽3米,深3米的长方体水池,这个水池占地 12 平方米.
【分析】由题意可知:求水池的占地面积,实际上是求上口的面积,水池的长和宽已知,利用长方形的面积公式即可求解.
【解答】解:4×3=12(平方米)
答:这个水池占地12平方米.
故答案为:12.
【点评】解答此题的关键是明白:求水池的占地面积,实际上是求上口的面积.
17.4个是 ;是 3 个.
【分析】根据分数的意义,有几个分数单位就是几分之几.
【解答】解:4个是 ;是 3个.
故答案为:,3.
【点评】本题考查了分数的意义和分数单位的意义,关键是找清楚有几个分数单位.
18.要观察病人的体温,用 折线 统计图表示比较合适.
【分析】折线统计图能明确看出病人的提问升降程度,便于观察,据此填空.
【解答】解:要观察病人的体温,用折线统计图表示比较合适.
故答案为:折线.
【点评】此题考查统计图的选择,根据实际情况,选择最能明显观察出问题的统计图.
三.判断题(共3小题)
19.一个数的最大因数是6,这个数的因数有4个. √ (判断对错)
【分析】首先根据:一个数的最大因数是6,可得:这个数是6;然后根据找一个数的因数,可以一对一对的找,把写成两个数的乘积,那么每一个乘积中的因数都是的因数,判断出这个数的因数有多少个即可.
【解答】解:因为一个数的最大因数是6,
所以这个数是6,
所以这个数的因数有4个:1、2、3、6,
所以题中说法正确.
故答案为:√.
【点评】此题主要考查了找一个数的因数的方法,要熟练掌握,解答此题的关键是要明确:一个数最大的因数是它本身.
20.两个不同的质数一定是互质数. √ .(判断对错)
【分析】质数只有1和它本身两个因数,互质数是两个数的公因数只有1,由此解答即可.
【解答】解:因为质数只有1和它本身两个因数,所以两个不同的质数一定是互质数;
故答案为:√.
【点评】解答此题主要是根据质数和互质数的意义进行判断.
21.合数都能被2整除. × .
【分析】合数的意义是:一个自然数如果除了1和它本身还有别的因数,这样的数叫做合数;能被2整除的数叫做偶数,能被2整除的数的特征是:个位上是0,2,4,6,8的数;由此解答.
【解答】解:合数都能被2整除这种说法是错误的.如,9、15、21等这些数是合数但是它们都不能被2整除.
故答案为:×.
【点评】此题的解答主要明确合数的意义,和能被2整除的数的特征.
四.计算题(共2小题)
22.计算:
【分析】按照从左向右的顺序进行计算。
【解答】解:
=2
=2
【点评】只含有一级运算的,按照从左向右的顺序进行计算。
23.计算:21
【分析】从左向右进行计算即可。
【解答】解:21
=21
=1
【点评】此题考查了分数的四则混合运算,注意运算顺序和运算法则。
五.应用题(共2小题)
24.国庆节期间,王老师一家自驾游去了离家380千米的某地,右面是他们离家的距离y(千米)与汽车行驶时间x(时)之间的关系图.
(1)他们出发30分钟时,离家多少千米?
(2)他们出发3小时时,离目的地还有多少千米?
【分析】(1)把30分钟化成0.5小时,2.5小时行驶了200千米,用200除以2.5求出速度,用速度乘0.5小时就是他们出发30分钟时,离家多少千米.
(2)观察图发现,2.5小时前后的速度不相同,用380千米减去200千米求出从2.5小时到4小时这段时间走的路程,然后再除以(4﹣2.5)小时求出这段时间的速度,再用这段时间的速度乘(3﹣2.5)小时求出(3﹣2.5)小时行驶的路程,再用380千米分别减去200千米和(3﹣2.5)小时行驶的路程就是离目的地还有多少千米.
【解答】解:(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米.
(2)(380﹣200)÷(4﹣2.5)×(3﹣2.5)
=180÷1.5×0.5
=60(千米)
380﹣200﹣60
=180﹣60
=120(千米)
答:离目的地还有120千米.
【点评】本题考查了速度、时间与路程关系式的应用,关键是根据2.5小时行驶了200千米求出速度.要注意2.5小时前后的速度不相同.
25.一个棱长7分米的正方体水槽里装满了水,把这些水倒入一个长10分米、宽7分米、高8分米的长方体水槽里(不计损耗),水槽里水深是多少?
【分析】利用正方体的体积计算公式,可以先求出正方体水槽内水的体积,把水全部倒进长方体的水槽里,水的体积没有变,因此用水的体积除以长方体的底面积解答即可。
【解答】解:(7×7×7)÷(10×7)
=343÷70
=4.9(分米)
答:水槽里水深是4.9分米。
【点评】此题属于应用长方体和正方体的体积计算公式解决实际问题,考查的目的是理解掌握长方体、正方体的体积计算及解决问题的能力。
六.解答题(共4小题)
26.在下面的方框里填上一个合适的数.
(1)48□,25□,是5的倍数又是2的倍数.
(2)24□,37□,是2的倍数又是3的倍数.
(3)10□,2□□,是5的倍数又是3的倍数.
【分析】(1)既是2的倍数又是5的倍数的数的特征是个位上是0,由此解答;
(2)是2的倍数又是3的倍数的数的特征是个位是偶数,且各位数字和是3的整数倍,或者这个数一定是2和3的最小公倍数6的整数倍,由此得解.
(3)是5的倍数又是3的倍数的数个位上要首先满足是5或0,然后分析是不是3的倍数.
【解答】解:(1)根据题意分析可得,既是2的倍数又是5的倍数的数的特征是个位上是0,即480,250.方框里填0,0.
答:方框里填写0,0符合题意,即480,250.
(2)由是2的倍数又是3的倍数的数的特征是个位是偶数,且各位数字和是3的整数倍,或者这个数一定是2和3的最小公倍数6的整数倍可得,240,372或378,由此可得.
答:方框里填写0,2或者8合适,即240,372或378.
(3)是5的倍数又是3的倍数的数个位上要满足是5或0,并且各位数字之和是3的倍数.分析可得105,225,255或者285.
答:方框里填写5,25(或者55,或者85).即105,225(或者255,或者285).
【点评】本题主要考查了是2,3,5的倍数的数字的特征,要熟练理解掌握.
27.请你把涂色部分用分数表示出来.
【分析】(1)把一个长方形的面积看作单位“1”,把它平均分成5份,每份是它的,其中2份涂色,表示.
(2)把一个圆的面积看作单位“1”,把它平均分成4份,每份是它的,其中3份涂色,表示.
(3)把一个正六边形的面积看作单位“1”,把它平均分成6份,每份是它的,其中5份涂色,表示.
【解答】解:把涂色部分用分数表示出来.
【点评】此题是考查分数的意义.把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数.
28.下列图形有几条对称轴?
【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此可以数出它们的对称轴.
【解答】解:
故答案为:1,1,1,2,2,5.
【点评】解答此题的主要依据是:轴对称图形的意义及其特征.注意画对称轴要用虚线.
29.做一个长方体抽屉,长40厘米,宽18厘米,高8厘米,至少需要木板多少平方分米?
【分析】首先要明确长方体木抽屉共有5个面,即四周的侧面加上一个底面就是本题要求的问题,注意单位名称的统一.
【解答】解:(40×8+18×8)×2+40×18
=(320+144)×2+720
=928+720
=1648(平方厘米),
1648平方厘米=16.48平方分米;
答;至少需要木板16.48平方分米.
【点评】把四周的面积加上一个底面积就是做一个这样抽屉需要的木板的面积
第1页(共1页)
同课章节目录
