2021-2022学年下学期上海市小学数学四年级期末典型试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年下学期上海市小学数学四年级期末典型试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 292.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览


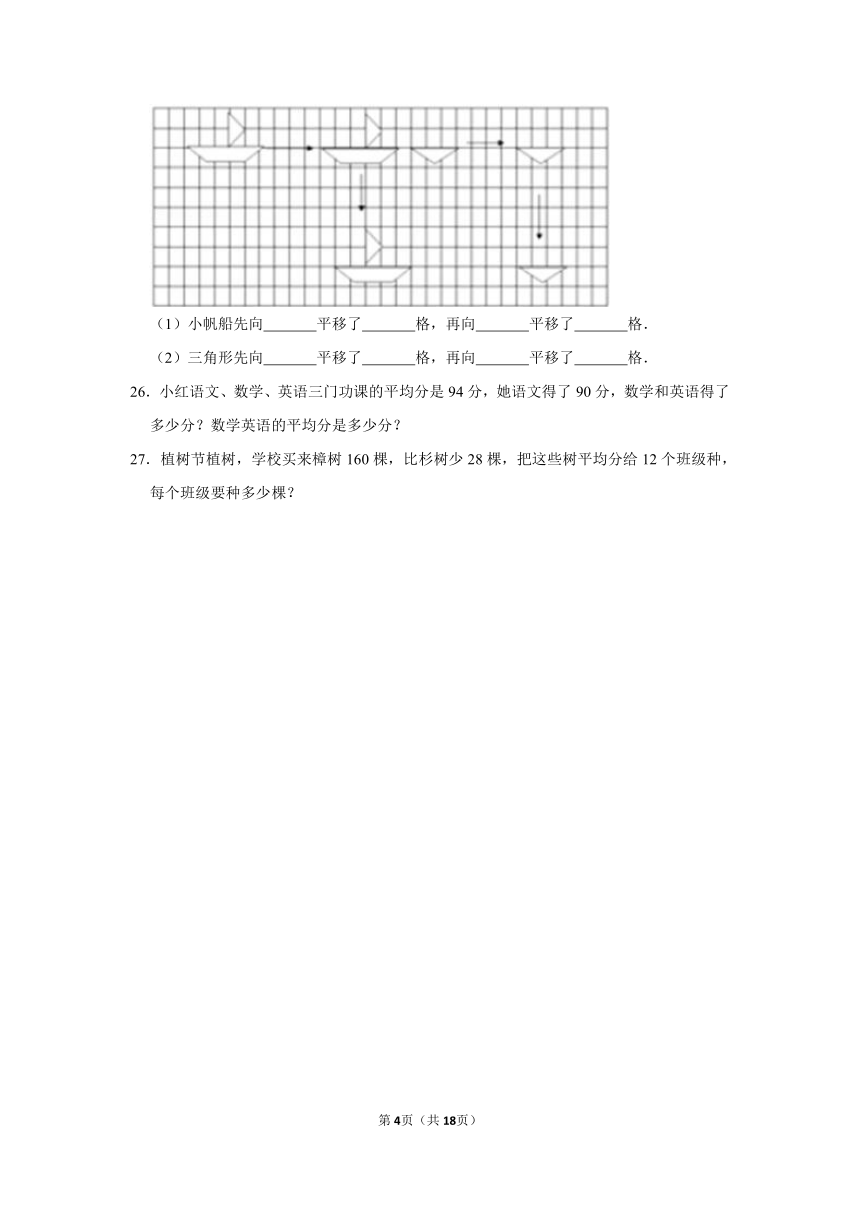

文档简介
2021-2022学年下学期上海市小学数学四年级期末典型试卷3
一.选择题(共7小题)
1.用800元可以买下面( )组的两样电器.
A. B.
C.
2.李华从正面看到的图形是( )
A. B.
C.
3.125×25×32=(125×8)×(25×4),这里运用了( )
A.乘法交换律
B.乘法结合律
C.乘法交换律和乘法结合律
4.把一个小数的小数点去掉后,比原数大39.6,这个小数是( )
A.3.96 B.3.6 C.4.4
5.下列图形中,最具有稳定性、不易变形的特性的是( )
A.三角形 B.平行四边形 C.正方形 D.长方形
6.某学校平均每班人数为43.4人,那么该学校的班级数可能是( )
A.18 B.27 C.24 D.25
7.100元钱买了100只鸟,大鸟3元钱一只,小鸟1元钱3只.大鸟买了( )只.
A.30 B.25 C.75 D.10
二.填空题(共7小题)
8.523× =523×100﹣523;
720÷ =72÷12=144÷ .
9.与9相邻的两位小数是 和
10. 的小数点向左移动三位,再向右移动两位后是2.45.
11.已知三角形的三个内角和为180°,∠B+∠C=105°,∠A= .
12.22.2最高位上的2比最低位上的2多 .
13.甲乙丙三数的平均数是12,则他们的和是 .
14.有鸡兔共9只,脚26只,鸡 只,兔 只.
三.判断题(共4小题)
15.如图,从前面看这个物体和从后面看这个物体,看到的图形是一样的. (判断对错)
16.把8×(11×125)改写成8×125×11是运用了乘法交换律和乘法结合律. .
17.大于0.1而小于0.9的小数有7个. .(判断对错)
18.在一个三角形中,如果有一个角是锐角,那么这个三角形就是锐角三角形. .(判断对错)
四.计算题(共2小题)
19.脱式计算.
32+(76﹣45)
48÷8+16
(503﹣458)×32
910﹣17×35
20.直接写出下列各题的得数
5+0.55= 4.08﹣0.8= ÷100=0.101
3.7÷100= 312÷3= 36×6÷36×6=
0.4﹣(0.4﹣0.1)= 5.2+6.7+4.8= (25﹣18+2)×4=
五.应用题(共2小题)
21.同学们乘车去秋游,每辆车可乘45人,前4辆车全部乘满,第五辆车还有17个空位.总共有多少人参加秋游?
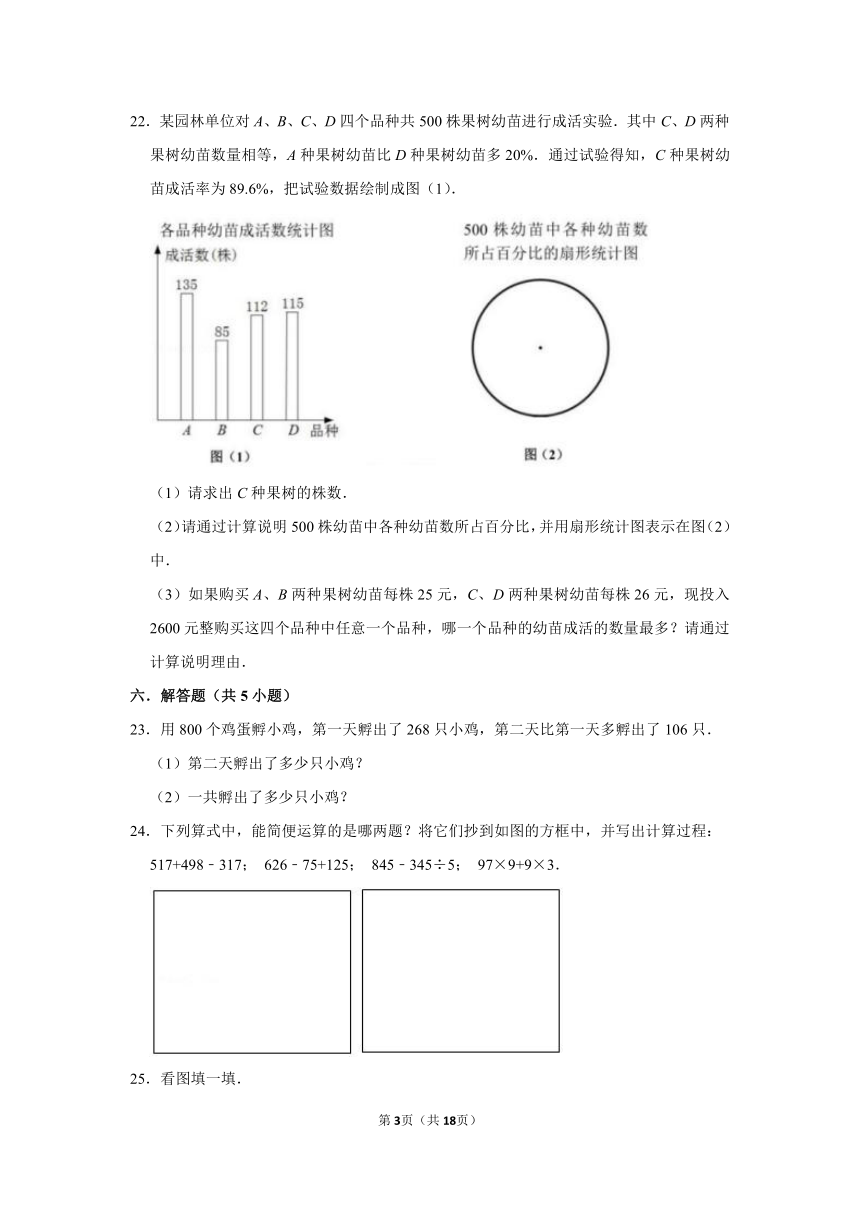
22.某园林单位对A、B、C、D四个品种共500株果树幼苗进行成活实验.其中C、D两种果树幼苗数量相等,A种果树幼苗比D种果树幼苗多20%.通过试验得知,C种果树幼苗成活率为89.6%,把试验数据绘制成图(1).
(1)请求出C种果树的株数.
(2)请通过计算说明500株幼苗中各种幼苗数所占百分比,并用扇形统计图表示在图(2)中.
(3)如果购买A、B两种果树幼苗每株25元,C、D两种果树幼苗每株26元,现投入2600元整购买这四个品种中任意一个品种,哪一个品种的幼苗成活的数量最多?请通过计算说明理由.
六.解答题(共5小题)
23.用800个鸡蛋孵小鸡,第一天孵出了268只小鸡,第二天比第一天多孵出了106只.
(1)第二天孵出了多少只小鸡?
(2)一共孵出了多少只小鸡?
24.下列算式中,能简便运算的是哪两题?将它们抄到如图的方框中,并写出计算过程:
517+498﹣317; 626﹣75+125; 845﹣345÷5; 97×9+9×3.
25.看图填一填.
(1)小帆船先向 平移了 格,再向 平移了 格.
(2)三角形先向 平移了 格,再向 平移了 格.
26.小红语文、数学、英语三门功课的平均分是94分,她语文得了90分,数学和英语得了多少分?数学英语的平均分是多少分?
27.植树节植树,学校买来樟树160棵,比杉树少28棵,把这些树平均分给12个班级种,每个班级要种多少棵?
2021-2022学年上海市人教新版四年级下学期期末典型试卷汇编3
参考答案与试题解析
一.选择题(共7小题)
1.用800元可以买下面( )组的两样电器.
A. B.
C.
【分析】运用估算的方法,把选项中两种商品的价格相加,求出和不大于800元即可.
【解答】解:A:598+195≈600+200=800(元)
598<600,195<200
所以598+195的准确值要小于800;
800元可以买到这两样电器.
B:398+488≈400+500=900(元)
900>800,所以800元不可以买到这两样电器.
C:406+417≈400+400=800(元)
406>400,417>400
所以406+417的准确值一定会大于800;
800元不可以买到这两样电器.
故选:A.
【点评】本题考查了学生根据加法估算的方法解决实际问题的能力.
2.李华从正面看到的图形是( )
A. B.
C.
【分析】先细心观察原立体图形中的圆柱体和正方体的位置关系,结合四个选项选出答案.
【解答】解:从正面可看到左边一个圆形,右边一个正方形,因此只有A的图形符合这个条件.
故选:A。
【点评】本题考查了从不同方向观察物体和几何体,主视图是从物体的正面看得到的视图.
3.125×25×32=(125×8)×(25×4),这里运用了( )
A.乘法交换律
B.乘法结合律
C.乘法交换律和乘法结合律
【分析】在125×25×32=(125×8)×(25×4)中,是把32看作8×4,然后用乘法交换律变成125×8×25×4,再运用乘法结合律计算,即(125×8)×(25×4).
【解答】解:125×25×32=(125×8)×(25×4),运用了乘法交换律和乘法结合律.
故选:C。
【点评】此题重点考查了学生对乘法交换律和结合律的掌握与运用情况.
4.把一个小数的小数点去掉后,比原数大39.6,这个小数是( )
A.3.96 B.3.6 C.4.4
【分析】由于把一个小数的小数点去掉后,比原数大39.6,可知原数是一位小数,原数的小数点去掉后是原数的10倍,则原数的小数点去掉后的数多10﹣1=9倍,可列算式39.6÷9求解.
【解答】解:39.6÷(10﹣1)
=39.6÷9
=4.4;
故选:C.
【点评】本题考查了小数点位置的移动与小数大小的变化规律,解题的关键是得到原数的小数点去掉后与原数的关系.
5.下列图形中,最具有稳定性、不易变形的特性的是( )
A.三角形 B.平行四边形 C.正方形 D.长方形
【分析】根据三角形具有稳定性,平行四边形具有易变性即可进行选择.
【解答】解:三角形具有不易变形的特性,平行四边形具有易变性,正方形、长方形都可以拉成平行四边形,所以也具有易变性;
故选:A.
【点评】本题考查三角形具有稳定性的特性,是基础题型.
6.某学校平均每班人数为43.4人,那么该学校的班级数可能是( )
A.18 B.27 C.24 D.25
【分析】根据“总人数=平均每班人数×班级个数”,由于五年级平均每班43.4人,在现实生活中,人数只能是整数,所以班级的个数只能是个位是0或5的数,据此解答.
【解答】解:由分析结合给出的四个数可知,
学校平均每班人数为43.4人,他们学校的班级数可能是25个班;
故选:D.
【点评】根据平均数的含义和生活实际进行解答.
7.100元钱买了100只鸟,大鸟3元钱一只,小鸟1元钱3只.大鸟买了( )只.
A.30 B.25 C.75 D.10
【分析】每只小鸟需要1÷3(元),假设全是大鸟,那么100只大鸟需要花100×3=300(元),实际少花了300﹣100=200(元),这是因为每只大鸟比每只小鸟多花(3)元,用多花的总钱数除以每只多花的钱数,即可求出小鸟的只数,进而求出大鸟的只数.
【解答】解:每只小鸟需要1÷3(元),
假设全是大鸟,那么小鸟有:
(100×3﹣100)÷(3)
=200
=75(只)
100﹣75=25(只)
答:大鸟买了25只.
故选:B.
【点评】此题属于鸡兔同笼题,解答此题的关键是先进行假设,然后根据假设后的情况进行计算,即可得出答案;也可以用方程解答,设其中的一个量为未知数,另一个数也用未知数表示,根据题意,列出方程,解答即可.
二.填空题(共7小题)
8.523× 99 =523×100﹣523;
720÷ 120 =72÷12=144÷ 24 .
【分析】(1)先把右面算式的后一个523看成523×1,再把它根据乘法分配律化简,得到前面的算式;
(2)根据商不变的规律,被除数和除数同时乘或除以一个相同的数(0除外),商不变;由此对72÷12中被除数的变化找出除数的变化,从而进行求解.
【解答】解:(1)523×100﹣523
=523×100﹣523×1
=523×(100﹣1)
=523×99
即:523×99=523×100﹣23;
(2)72÷12
=(72×10)÷(12×10)
=720÷120
(2)72÷12
=(72×2)÷(12×2)
=144÷24
即:720÷120=72÷12=144÷24.
故答案为:99;120,24.
【点评】本题考查了乘法分配律和商不变规律的灵活运用.
9.与9相邻的两位小数是 8.99 和 9.01
【分析】根据相邻的两个两位小数之间相差0.01,据此进行解答即可.
【解答】解:9﹣0.01=8.99
9+0.01=9.01
所以与9相邻的两位小数是 8.99和 9.01;
故答案为:8.99,9.01.
【点评】解答此题应明确:相邻的两个两位小数之间相差0.01.
10. 24.5 的小数点向左移动三位,再向右移动两位后是2.45.
【分析】此题可逆向思考即把2.45缩小100倍,再扩大1000倍是多少,根据小数点位置移动引起数的大小变化规律解答.
【解答】解:2.45÷100×1000=24.5
答:这个数原来是24.5;
故答案为:24.5.
【点评】此题考查小数点位置移动引起数的大小变化规律:把一个数扩大(或缩小)10倍、100倍、1000倍…只要把这个数的小数点向右(或向左)移动一位、两位、三位…,反之也成立.
11.已知三角形的三个内角和为180°,∠B+∠C=105°,∠A= 75° .
【分析】根据三角形的内角和=180°,由180°﹣两个内角的和=另一个内角的度数,据此解答即可.
【解答】解:180°﹣105°=75°
答:∠A的度数是75°.
故答案为:75°.
【点评】本题主要考查了对三角形的内角和=180°的理解和灵活运用情况.
12.22.2最高位上的2比最低位上的2多 19.8 .
【分析】22.2这个数的最高位是十位,最高位上的“2”表示2个十;最低位是十分位,最低位上的“2”表示2个0.1,进一步算出两个“2”表示的数相差多少即可.
【解答】解:最高位上的“2”表示2个十,最低位上的“2”表示2个0.1,
20﹣0.2=19.8.
答:22.2最高位上的2比最低位上的2多19.8.
故答案为:19.8.
【点评】此题考查小数、整数中的数字所表示的意义,关键是看此数字在哪一个数位上和计数单位是什么,就有几个计数单位,进而得解.
13.甲乙丙三数的平均数是12,则他们的和是 36 .
【分析】根据“总数=平均数×数量”,即可计算出甲、乙、丙三个数的和.
【解答】解:12×3=36;
答:他们的和是 36.
故答案为:36.
【点评】解答此题用到的知识点:平均数、数量和总数三者之间的关系.
14.有鸡兔共9只,脚26只,鸡 5 只,兔 4 只.
【分析】假设都是鸡,那么就有9×2=18只脚,这样就多出26﹣18=8只脚;因为一只兔比一只鸡多4﹣2=2只脚,也就是有8÷2=4只兔;进而求得鸡的只数.
【解答】解:兔:(26﹣9×2)÷(4﹣2)
=8÷2
=4(只)
鸡:9﹣4=5(只);
答:鸡有5只,兔有4只.
故答案为:5,4.
【点评】此题属于典型的鸡兔同笼问题,解答此类题的关键是用假设法,也可以用方程进行解答.
三.判断题(共4小题)
15.如图,从前面看这个物体和从后面看这个物体,看到的图形是一样的. × (判断对错)
【分析】从前面看这个物体是横着的两个小正方形,左面上方一个小正方形,从后面看这个物体是横着的两个小正方形,右面上方一个小正方形,由此判断即可.
【解答】解:因为从前面看这个物体是横着的两个小正方形,左面上方一个小正方形,从后面看这个物体是横着的两个小正方形,右面上方一个小正方形,
所以看到的图形是不一样的.原题错误.
故答案为:×.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
16.把8×(11×125)改写成8×125×11是运用了乘法交换律和乘法结合律. √ .
【分析】8×(11×125)改写成8×125×11先运用乘法交换律,交换11和125的位置,变成8×(125×11),再运用乘法结合律把8×125结合在一起.
【解答】解:8×(11×125),
=8×(125×11),
=8×125×11,
=1000×11,
=11000;
这是运用了乘法交换律和乘法结合律简算.
故答案为:√.
【点评】运算定律是常用的简便运算的方法,要熟练掌握,灵活运用.
17.大于0.1而小于0.9的小数有7个. × .(判断对错)
【分析】根据小数大小比较的方法,大于0.1而小于0.9的一位小数有:0.2、0.3、0.4、0.5、…,大于0.1而小于0.9的两位小数有:0.21、0.31、0.41、0.51、…,大于0.1而小于0.9的三位小数有:0.211、0.311、0.411、0.511、…,…,所以大于0.1而小于0.9的小数有无数个,据此判断即可.
【解答】解:大于0.1而小于0.9的一位小数有:0.2、0.3、0.4、0.5、…,
大于0.1而小于0.9的两位小数有:0.21、0.31、0.41、0.51、…,
大于0.1而小于0.9的三位小数有:0.211、0.311、0.411、0.511、…,…,
所以大于0.1而小于0.9的小数有无数个,
所以题中说法不正确.
故答案为:×.
【点评】此题主要考查了小数比较大小的方法的应用,要熟练掌握.
18.在一个三角形中,如果有一个角是锐角,那么这个三角形就是锐角三角形. × .(判断对错)
【分析】根据锐角三角形的含义:三个角都是锐角的三角形是锐角三角形,进行判断即可.
【解答】解:根据三角形的分类可知:在一个三角形中,如果有一个角是锐角,可能是锐角三角形、直角三角形,也可能是钝角三角形,所以如果有一个角是锐角,那么这个三角形就是锐角三角形,说法错误;
故答案为:×.
【点评】解答此题应根据锐角三角形的含义进行解答.
四.计算题(共2小题)
19.脱式计算.
32+(76﹣45)
48÷8+16
(503﹣458)×32
910﹣17×35
【分析】(1)先算小括号里面的减法,再算括号外的加法;
(2)先算除法,再算加法;
(3)先算小括号里面的减法,再算括号外的乘法;
(4)先算乘法,再算减法.
【解答】解:(1)32+(76﹣45)
=32+31
=63
(2)48÷8+16
=6+16
=26
(3)(503﹣458)×32
=45×32
=1440
(4)910﹣17×35
=910﹣595
=315
【点评】本题考查了简单的四则混合运算,计算时先理清楚运算顺序,根据运算顺序逐步求解即可.
20.直接写出下列各题的得数
5+0.55= 4.08﹣0.8= 10.1 ÷100=0.101
3.7÷100= 312÷3= 36×6÷36×6=
0.4﹣(0.4﹣0.1)= 5.2+6.7+4.8= (25﹣18+2)×4=
【分析】根据小数的加法、减法、乘法、除法的计算方法进行计算.第三小题根据被除数=除数×商进行计算.
【解答】解:
5+0.55=5.55 4.08﹣0.8=3.28 10.1÷100=0.101
3.7÷100=0.037 312÷3=104 36×6÷36×6=36
0.4﹣(0.4﹣0.1)=0.1 5.2+6.7+4.8=16.7 (25﹣18+2)×4=20
【点评】本题考查的是小数运算方法的运用,掌握正确的计算方法是解答本题的关键.
五.应用题(共2小题)
21.同学们乘车去秋游,每辆车可乘45人,前4辆车全部乘满,第五辆车还有17个空位.总共有多少人参加秋游?
【分析】每辆车可乘45人,前4辆车全部乘满,根据乘法的意义,前四辆共坐了45×4人,又第5辆车还有17个空位,则第五辆上坐了45﹣17人,所以共有学生45×4+(45﹣17)人.
【解答】解:45×4+(45﹣17)
=180+28
=208(人)
答:总共有208人参加秋游.
【点评】完成本题要注意第5辆车还有17个空位,而不是坐了17人.
22.某园林单位对A、B、C、D四个品种共500株果树幼苗进行成活实验.其中C、D两种果树幼苗数量相等,A种果树幼苗比D种果树幼苗多20%.通过试验得知,C种果树幼苗成活率为89.6%,把试验数据绘制成图(1).
(1)请求出C种果树的株数.
(2)请通过计算说明500株幼苗中各种幼苗数所占百分比,并用扇形统计图表示在图(2)中.
(3)如果购买A、B两种果树幼苗每株25元,C、D两种果树幼苗每株26元,现投入2600元整购买这四个品种中任意一个品种,哪一个品种的幼苗成活的数量最多?请通过计算说明理由.
【分析】(1)已知C种果树幼苗成活率为89.6%,成活了135棵,根据已知一个数的百分之几是多少,求这个数,用除法求出C种果树的株数.
(2)因为C、D两种果树幼苗数量相等,所以D种果树幼苗的株数为125棵;
A种果树幼苗比D种果树幼苗多20%.把D 种果树苗的棵数看作单位“1”,A种果树苗的棵数相当于D 种果树的(1+20%),根据一个数是乘百分数的意义,用乘法求出A种果树苗的棵数;关键减法的意义,用减法求出B 种果树苗的棵数;把四种公式苗的总数看作单位“1”,根据求一个数是另一个数的百分之几,用除法求出各种果树苗的棵数各占总数的百分比,据此完成扇形统计图.
(3)已知C种果树幼苗成活率为89.6%,根据求成活率的方法分别求出A、B、D三种果树苗的成活率,根据百分数大小比较的方法,把四种果树苗的成活率进行比较,选择成活率最高的哪一种.据此解答.
【解答】解:(1)112÷89.6
=112÷0.896
=125(株)
答:C种果树苗有125株.
(2)因为C、D两种果树幼苗数量相等,所以D种果树幼苗的株数为125棵;
A种:125×(1+20%)
=125×1.2
=150(株)
B 种:500﹣(125+125+150)
=500﹣400
=100(株)
A种果树苗占的百分率:100%
=0.3×100%
=30%
B种果树苗占的百分率:100%
=0.2×100%
=20%
C、D种果树苗占的百分率:100%
=0.25×100%
=25%
作图如下:
(3)A种成活率:100%=90%
B种成活率:100%=85%
D种成活率:100%=92%
因为90%>85%,92%>89.6%,所以只需要比较AD两种即可
A种果树苗成活的棵数为:2600÷25×90%
=104×0.9
=93.6(株)
D种果树苗的成活的株数为:2600÷26×92%
=100×0.92
=92(株)
因为93.6株>92株
所以投入2600元整购买A种果树苗成活数量最多.
【点评】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
六.解答题(共5小题)
23.用800个鸡蛋孵小鸡,第一天孵出了268只小鸡,第二天比第一天多孵出了106只.
(1)第二天孵出了多少只小鸡?
(2)一共孵出了多少只小鸡?
【分析】(1)第一天孵出了268只小鸡,第二天比第一天多孵出了106只,就是比268多106,即(268+106)只,解答即可;
(2)用第一天孵出的加上第二天孵出的就是一共孵出的只数.
【解答】解:(1)268+106=374(只)
答:第二天孵出了374只小鸡.
(2)374+268=642(只)
答:一共孵出了642只小鸡.
【点评】本题考查了学生根据加法的意义列式解答应用题的能力.
24.下列算式中,能简便运算的是哪两题?将它们抄到如图的方框中,并写出计算过程:
517+498﹣317; 626﹣75+125; 845﹣345÷5; 97×9+9×3.
【分析】517+498﹣317运用加法的交换律进行简算; 97×9+9×3运用乘法的分配律进行简算;626﹣75+125从左向右进行计算;845﹣345÷5先算除法,再算减法.
【解答】解:
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
25.看图填一填.
(1)小帆船先向 右 平移了 9 格,再向 下 平移了 6 格.
(2)三角形先向 右 平移了 7 格,再向 下 平移了 6 格.
【分析】根据图形平移的意义,在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,属于平移现象.
【解答】解:(1)小帆船先向右平移了9格,再向下平移了6格.
(2)三角形先向右平移了7格,再向下平移了6格.
故答案为:右,9,下,6;右,7,下,6.
【点评】本题是考查平移的意义.
26.小红语文、数学、英语三门功课的平均分是94分,她语文得了90分,数学和英语得了多少分?数学英语的平均分是多少分?
【分析】根据“平均成绩×科目的数量=总成绩”算出语文、数学、英语三门功课的总成绩,进而用“语文、数学、英语三门功课的总成绩分别减去语文功课的成绩,即可求出数学和英语得了多少分,再除以2即可.
【解答】解:94×3﹣90,
=282﹣90,
=192(分);
答:数学和英语得了192分.
192÷2=96(分);
答:数学英语的平均分是96分.
【点评】解答此题的关键是:先根据平均数的计算方法求出三门课程的总成绩,然后分别减去语文的成绩,进而解答即可.
27.植树节植树,学校买来樟树160棵,比杉树少28棵,把这些树平均分给12个班级种,每个班级要种多少棵?
【分析】由题意,先用加法求得植树的总棵数,用植树的总棵数除以总班数,就是平均每个班植的棵数,据此解答.
【解答】解:(160+28+160)÷12
=348÷12
=29(棵)
答:平均每个班要种29棵.
【点评】本题依据除法平均分的意义列式求解即可
第1页(共1页)
一.选择题(共7小题)
1.用800元可以买下面( )组的两样电器.
A. B.
C.
2.李华从正面看到的图形是( )
A. B.
C.
3.125×25×32=(125×8)×(25×4),这里运用了( )
A.乘法交换律
B.乘法结合律
C.乘法交换律和乘法结合律
4.把一个小数的小数点去掉后,比原数大39.6,这个小数是( )
A.3.96 B.3.6 C.4.4
5.下列图形中,最具有稳定性、不易变形的特性的是( )
A.三角形 B.平行四边形 C.正方形 D.长方形
6.某学校平均每班人数为43.4人,那么该学校的班级数可能是( )
A.18 B.27 C.24 D.25
7.100元钱买了100只鸟,大鸟3元钱一只,小鸟1元钱3只.大鸟买了( )只.
A.30 B.25 C.75 D.10
二.填空题(共7小题)
8.523× =523×100﹣523;
720÷ =72÷12=144÷ .
9.与9相邻的两位小数是 和
10. 的小数点向左移动三位,再向右移动两位后是2.45.
11.已知三角形的三个内角和为180°,∠B+∠C=105°,∠A= .
12.22.2最高位上的2比最低位上的2多 .
13.甲乙丙三数的平均数是12,则他们的和是 .
14.有鸡兔共9只,脚26只,鸡 只,兔 只.
三.判断题(共4小题)
15.如图,从前面看这个物体和从后面看这个物体,看到的图形是一样的. (判断对错)
16.把8×(11×125)改写成8×125×11是运用了乘法交换律和乘法结合律. .
17.大于0.1而小于0.9的小数有7个. .(判断对错)
18.在一个三角形中,如果有一个角是锐角,那么这个三角形就是锐角三角形. .(判断对错)
四.计算题(共2小题)
19.脱式计算.
32+(76﹣45)
48÷8+16
(503﹣458)×32
910﹣17×35
20.直接写出下列各题的得数
5+0.55= 4.08﹣0.8= ÷100=0.101
3.7÷100= 312÷3= 36×6÷36×6=
0.4﹣(0.4﹣0.1)= 5.2+6.7+4.8= (25﹣18+2)×4=
五.应用题(共2小题)
21.同学们乘车去秋游,每辆车可乘45人,前4辆车全部乘满,第五辆车还有17个空位.总共有多少人参加秋游?
22.某园林单位对A、B、C、D四个品种共500株果树幼苗进行成活实验.其中C、D两种果树幼苗数量相等,A种果树幼苗比D种果树幼苗多20%.通过试验得知,C种果树幼苗成活率为89.6%,把试验数据绘制成图(1).
(1)请求出C种果树的株数.
(2)请通过计算说明500株幼苗中各种幼苗数所占百分比,并用扇形统计图表示在图(2)中.
(3)如果购买A、B两种果树幼苗每株25元,C、D两种果树幼苗每株26元,现投入2600元整购买这四个品种中任意一个品种,哪一个品种的幼苗成活的数量最多?请通过计算说明理由.
六.解答题(共5小题)
23.用800个鸡蛋孵小鸡,第一天孵出了268只小鸡,第二天比第一天多孵出了106只.
(1)第二天孵出了多少只小鸡?
(2)一共孵出了多少只小鸡?
24.下列算式中,能简便运算的是哪两题?将它们抄到如图的方框中,并写出计算过程:
517+498﹣317; 626﹣75+125; 845﹣345÷5; 97×9+9×3.
25.看图填一填.
(1)小帆船先向 平移了 格,再向 平移了 格.
(2)三角形先向 平移了 格,再向 平移了 格.
26.小红语文、数学、英语三门功课的平均分是94分,她语文得了90分,数学和英语得了多少分?数学英语的平均分是多少分?
27.植树节植树,学校买来樟树160棵,比杉树少28棵,把这些树平均分给12个班级种,每个班级要种多少棵?
2021-2022学年上海市人教新版四年级下学期期末典型试卷汇编3
参考答案与试题解析
一.选择题(共7小题)
1.用800元可以买下面( )组的两样电器.
A. B.
C.
【分析】运用估算的方法,把选项中两种商品的价格相加,求出和不大于800元即可.
【解答】解:A:598+195≈600+200=800(元)
598<600,195<200
所以598+195的准确值要小于800;
800元可以买到这两样电器.
B:398+488≈400+500=900(元)
900>800,所以800元不可以买到这两样电器.
C:406+417≈400+400=800(元)
406>400,417>400
所以406+417的准确值一定会大于800;
800元不可以买到这两样电器.
故选:A.
【点评】本题考查了学生根据加法估算的方法解决实际问题的能力.
2.李华从正面看到的图形是( )
A. B.
C.
【分析】先细心观察原立体图形中的圆柱体和正方体的位置关系,结合四个选项选出答案.
【解答】解:从正面可看到左边一个圆形,右边一个正方形,因此只有A的图形符合这个条件.
故选:A。
【点评】本题考查了从不同方向观察物体和几何体,主视图是从物体的正面看得到的视图.
3.125×25×32=(125×8)×(25×4),这里运用了( )
A.乘法交换律
B.乘法结合律
C.乘法交换律和乘法结合律
【分析】在125×25×32=(125×8)×(25×4)中,是把32看作8×4,然后用乘法交换律变成125×8×25×4,再运用乘法结合律计算,即(125×8)×(25×4).
【解答】解:125×25×32=(125×8)×(25×4),运用了乘法交换律和乘法结合律.
故选:C。
【点评】此题重点考查了学生对乘法交换律和结合律的掌握与运用情况.
4.把一个小数的小数点去掉后,比原数大39.6,这个小数是( )
A.3.96 B.3.6 C.4.4
【分析】由于把一个小数的小数点去掉后,比原数大39.6,可知原数是一位小数,原数的小数点去掉后是原数的10倍,则原数的小数点去掉后的数多10﹣1=9倍,可列算式39.6÷9求解.
【解答】解:39.6÷(10﹣1)
=39.6÷9
=4.4;
故选:C.
【点评】本题考查了小数点位置的移动与小数大小的变化规律,解题的关键是得到原数的小数点去掉后与原数的关系.
5.下列图形中,最具有稳定性、不易变形的特性的是( )
A.三角形 B.平行四边形 C.正方形 D.长方形
【分析】根据三角形具有稳定性,平行四边形具有易变性即可进行选择.
【解答】解:三角形具有不易变形的特性,平行四边形具有易变性,正方形、长方形都可以拉成平行四边形,所以也具有易变性;
故选:A.
【点评】本题考查三角形具有稳定性的特性,是基础题型.
6.某学校平均每班人数为43.4人,那么该学校的班级数可能是( )
A.18 B.27 C.24 D.25
【分析】根据“总人数=平均每班人数×班级个数”,由于五年级平均每班43.4人,在现实生活中,人数只能是整数,所以班级的个数只能是个位是0或5的数,据此解答.
【解答】解:由分析结合给出的四个数可知,
学校平均每班人数为43.4人,他们学校的班级数可能是25个班;
故选:D.
【点评】根据平均数的含义和生活实际进行解答.
7.100元钱买了100只鸟,大鸟3元钱一只,小鸟1元钱3只.大鸟买了( )只.
A.30 B.25 C.75 D.10
【分析】每只小鸟需要1÷3(元),假设全是大鸟,那么100只大鸟需要花100×3=300(元),实际少花了300﹣100=200(元),这是因为每只大鸟比每只小鸟多花(3)元,用多花的总钱数除以每只多花的钱数,即可求出小鸟的只数,进而求出大鸟的只数.
【解答】解:每只小鸟需要1÷3(元),
假设全是大鸟,那么小鸟有:
(100×3﹣100)÷(3)
=200
=75(只)
100﹣75=25(只)
答:大鸟买了25只.
故选:B.
【点评】此题属于鸡兔同笼题,解答此题的关键是先进行假设,然后根据假设后的情况进行计算,即可得出答案;也可以用方程解答,设其中的一个量为未知数,另一个数也用未知数表示,根据题意,列出方程,解答即可.
二.填空题(共7小题)
8.523× 99 =523×100﹣523;
720÷ 120 =72÷12=144÷ 24 .
【分析】(1)先把右面算式的后一个523看成523×1,再把它根据乘法分配律化简,得到前面的算式;
(2)根据商不变的规律,被除数和除数同时乘或除以一个相同的数(0除外),商不变;由此对72÷12中被除数的变化找出除数的变化,从而进行求解.
【解答】解:(1)523×100﹣523
=523×100﹣523×1
=523×(100﹣1)
=523×99
即:523×99=523×100﹣23;
(2)72÷12
=(72×10)÷(12×10)
=720÷120
(2)72÷12
=(72×2)÷(12×2)
=144÷24
即:720÷120=72÷12=144÷24.
故答案为:99;120,24.
【点评】本题考查了乘法分配律和商不变规律的灵活运用.
9.与9相邻的两位小数是 8.99 和 9.01
【分析】根据相邻的两个两位小数之间相差0.01,据此进行解答即可.
【解答】解:9﹣0.01=8.99
9+0.01=9.01
所以与9相邻的两位小数是 8.99和 9.01;
故答案为:8.99,9.01.
【点评】解答此题应明确:相邻的两个两位小数之间相差0.01.
10. 24.5 的小数点向左移动三位,再向右移动两位后是2.45.
【分析】此题可逆向思考即把2.45缩小100倍,再扩大1000倍是多少,根据小数点位置移动引起数的大小变化规律解答.
【解答】解:2.45÷100×1000=24.5
答:这个数原来是24.5;
故答案为:24.5.
【点评】此题考查小数点位置移动引起数的大小变化规律:把一个数扩大(或缩小)10倍、100倍、1000倍…只要把这个数的小数点向右(或向左)移动一位、两位、三位…,反之也成立.
11.已知三角形的三个内角和为180°,∠B+∠C=105°,∠A= 75° .
【分析】根据三角形的内角和=180°,由180°﹣两个内角的和=另一个内角的度数,据此解答即可.
【解答】解:180°﹣105°=75°
答:∠A的度数是75°.
故答案为:75°.
【点评】本题主要考查了对三角形的内角和=180°的理解和灵活运用情况.
12.22.2最高位上的2比最低位上的2多 19.8 .
【分析】22.2这个数的最高位是十位,最高位上的“2”表示2个十;最低位是十分位,最低位上的“2”表示2个0.1,进一步算出两个“2”表示的数相差多少即可.
【解答】解:最高位上的“2”表示2个十,最低位上的“2”表示2个0.1,
20﹣0.2=19.8.
答:22.2最高位上的2比最低位上的2多19.8.
故答案为:19.8.
【点评】此题考查小数、整数中的数字所表示的意义,关键是看此数字在哪一个数位上和计数单位是什么,就有几个计数单位,进而得解.
13.甲乙丙三数的平均数是12,则他们的和是 36 .
【分析】根据“总数=平均数×数量”,即可计算出甲、乙、丙三个数的和.
【解答】解:12×3=36;
答:他们的和是 36.
故答案为:36.
【点评】解答此题用到的知识点:平均数、数量和总数三者之间的关系.
14.有鸡兔共9只,脚26只,鸡 5 只,兔 4 只.
【分析】假设都是鸡,那么就有9×2=18只脚,这样就多出26﹣18=8只脚;因为一只兔比一只鸡多4﹣2=2只脚,也就是有8÷2=4只兔;进而求得鸡的只数.
【解答】解:兔:(26﹣9×2)÷(4﹣2)
=8÷2
=4(只)
鸡:9﹣4=5(只);
答:鸡有5只,兔有4只.
故答案为:5,4.
【点评】此题属于典型的鸡兔同笼问题,解答此类题的关键是用假设法,也可以用方程进行解答.
三.判断题(共4小题)
15.如图,从前面看这个物体和从后面看这个物体,看到的图形是一样的. × (判断对错)
【分析】从前面看这个物体是横着的两个小正方形,左面上方一个小正方形,从后面看这个物体是横着的两个小正方形,右面上方一个小正方形,由此判断即可.
【解答】解:因为从前面看这个物体是横着的两个小正方形,左面上方一个小正方形,从后面看这个物体是横着的两个小正方形,右面上方一个小正方形,
所以看到的图形是不一样的.原题错误.
故答案为:×.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
16.把8×(11×125)改写成8×125×11是运用了乘法交换律和乘法结合律. √ .
【分析】8×(11×125)改写成8×125×11先运用乘法交换律,交换11和125的位置,变成8×(125×11),再运用乘法结合律把8×125结合在一起.
【解答】解:8×(11×125),
=8×(125×11),
=8×125×11,
=1000×11,
=11000;
这是运用了乘法交换律和乘法结合律简算.
故答案为:√.
【点评】运算定律是常用的简便运算的方法,要熟练掌握,灵活运用.
17.大于0.1而小于0.9的小数有7个. × .(判断对错)
【分析】根据小数大小比较的方法,大于0.1而小于0.9的一位小数有:0.2、0.3、0.4、0.5、…,大于0.1而小于0.9的两位小数有:0.21、0.31、0.41、0.51、…,大于0.1而小于0.9的三位小数有:0.211、0.311、0.411、0.511、…,…,所以大于0.1而小于0.9的小数有无数个,据此判断即可.
【解答】解:大于0.1而小于0.9的一位小数有:0.2、0.3、0.4、0.5、…,
大于0.1而小于0.9的两位小数有:0.21、0.31、0.41、0.51、…,
大于0.1而小于0.9的三位小数有:0.211、0.311、0.411、0.511、…,…,
所以大于0.1而小于0.9的小数有无数个,
所以题中说法不正确.
故答案为:×.
【点评】此题主要考查了小数比较大小的方法的应用,要熟练掌握.
18.在一个三角形中,如果有一个角是锐角,那么这个三角形就是锐角三角形. × .(判断对错)
【分析】根据锐角三角形的含义:三个角都是锐角的三角形是锐角三角形,进行判断即可.
【解答】解:根据三角形的分类可知:在一个三角形中,如果有一个角是锐角,可能是锐角三角形、直角三角形,也可能是钝角三角形,所以如果有一个角是锐角,那么这个三角形就是锐角三角形,说法错误;
故答案为:×.
【点评】解答此题应根据锐角三角形的含义进行解答.
四.计算题(共2小题)
19.脱式计算.
32+(76﹣45)
48÷8+16
(503﹣458)×32
910﹣17×35
【分析】(1)先算小括号里面的减法,再算括号外的加法;
(2)先算除法,再算加法;
(3)先算小括号里面的减法,再算括号外的乘法;
(4)先算乘法,再算减法.
【解答】解:(1)32+(76﹣45)
=32+31
=63
(2)48÷8+16
=6+16
=26
(3)(503﹣458)×32
=45×32
=1440
(4)910﹣17×35
=910﹣595
=315
【点评】本题考查了简单的四则混合运算,计算时先理清楚运算顺序,根据运算顺序逐步求解即可.
20.直接写出下列各题的得数
5+0.55= 4.08﹣0.8= 10.1 ÷100=0.101
3.7÷100= 312÷3= 36×6÷36×6=
0.4﹣(0.4﹣0.1)= 5.2+6.7+4.8= (25﹣18+2)×4=
【分析】根据小数的加法、减法、乘法、除法的计算方法进行计算.第三小题根据被除数=除数×商进行计算.
【解答】解:
5+0.55=5.55 4.08﹣0.8=3.28 10.1÷100=0.101
3.7÷100=0.037 312÷3=104 36×6÷36×6=36
0.4﹣(0.4﹣0.1)=0.1 5.2+6.7+4.8=16.7 (25﹣18+2)×4=20
【点评】本题考查的是小数运算方法的运用,掌握正确的计算方法是解答本题的关键.
五.应用题(共2小题)
21.同学们乘车去秋游,每辆车可乘45人,前4辆车全部乘满,第五辆车还有17个空位.总共有多少人参加秋游?
【分析】每辆车可乘45人,前4辆车全部乘满,根据乘法的意义,前四辆共坐了45×4人,又第5辆车还有17个空位,则第五辆上坐了45﹣17人,所以共有学生45×4+(45﹣17)人.
【解答】解:45×4+(45﹣17)
=180+28
=208(人)
答:总共有208人参加秋游.
【点评】完成本题要注意第5辆车还有17个空位,而不是坐了17人.
22.某园林单位对A、B、C、D四个品种共500株果树幼苗进行成活实验.其中C、D两种果树幼苗数量相等,A种果树幼苗比D种果树幼苗多20%.通过试验得知,C种果树幼苗成活率为89.6%,把试验数据绘制成图(1).
(1)请求出C种果树的株数.
(2)请通过计算说明500株幼苗中各种幼苗数所占百分比,并用扇形统计图表示在图(2)中.
(3)如果购买A、B两种果树幼苗每株25元,C、D两种果树幼苗每株26元,现投入2600元整购买这四个品种中任意一个品种,哪一个品种的幼苗成活的数量最多?请通过计算说明理由.
【分析】(1)已知C种果树幼苗成活率为89.6%,成活了135棵,根据已知一个数的百分之几是多少,求这个数,用除法求出C种果树的株数.
(2)因为C、D两种果树幼苗数量相等,所以D种果树幼苗的株数为125棵;
A种果树幼苗比D种果树幼苗多20%.把D 种果树苗的棵数看作单位“1”,A种果树苗的棵数相当于D 种果树的(1+20%),根据一个数是乘百分数的意义,用乘法求出A种果树苗的棵数;关键减法的意义,用减法求出B 种果树苗的棵数;把四种公式苗的总数看作单位“1”,根据求一个数是另一个数的百分之几,用除法求出各种果树苗的棵数各占总数的百分比,据此完成扇形统计图.
(3)已知C种果树幼苗成活率为89.6%,根据求成活率的方法分别求出A、B、D三种果树苗的成活率,根据百分数大小比较的方法,把四种果树苗的成活率进行比较,选择成活率最高的哪一种.据此解答.
【解答】解:(1)112÷89.6
=112÷0.896
=125(株)
答:C种果树苗有125株.
(2)因为C、D两种果树幼苗数量相等,所以D种果树幼苗的株数为125棵;
A种:125×(1+20%)
=125×1.2
=150(株)
B 种:500﹣(125+125+150)
=500﹣400
=100(株)
A种果树苗占的百分率:100%
=0.3×100%
=30%
B种果树苗占的百分率:100%
=0.2×100%
=20%
C、D种果树苗占的百分率:100%
=0.25×100%
=25%
作图如下:
(3)A种成活率:100%=90%
B种成活率:100%=85%
D种成活率:100%=92%
因为90%>85%,92%>89.6%,所以只需要比较AD两种即可
A种果树苗成活的棵数为:2600÷25×90%
=104×0.9
=93.6(株)
D种果树苗的成活的株数为:2600÷26×92%
=100×0.92
=92(株)
因为93.6株>92株
所以投入2600元整购买A种果树苗成活数量最多.
【点评】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
六.解答题(共5小题)
23.用800个鸡蛋孵小鸡,第一天孵出了268只小鸡,第二天比第一天多孵出了106只.
(1)第二天孵出了多少只小鸡?
(2)一共孵出了多少只小鸡?
【分析】(1)第一天孵出了268只小鸡,第二天比第一天多孵出了106只,就是比268多106,即(268+106)只,解答即可;
(2)用第一天孵出的加上第二天孵出的就是一共孵出的只数.
【解答】解:(1)268+106=374(只)
答:第二天孵出了374只小鸡.
(2)374+268=642(只)
答:一共孵出了642只小鸡.
【点评】本题考查了学生根据加法的意义列式解答应用题的能力.
24.下列算式中,能简便运算的是哪两题?将它们抄到如图的方框中,并写出计算过程:
517+498﹣317; 626﹣75+125; 845﹣345÷5; 97×9+9×3.
【分析】517+498﹣317运用加法的交换律进行简算; 97×9+9×3运用乘法的分配律进行简算;626﹣75+125从左向右进行计算;845﹣345÷5先算除法,再算减法.
【解答】解:
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
25.看图填一填.
(1)小帆船先向 右 平移了 9 格,再向 下 平移了 6 格.
(2)三角形先向 右 平移了 7 格,再向 下 平移了 6 格.
【分析】根据图形平移的意义,在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,属于平移现象.
【解答】解:(1)小帆船先向右平移了9格,再向下平移了6格.
(2)三角形先向右平移了7格,再向下平移了6格.
故答案为:右,9,下,6;右,7,下,6.
【点评】本题是考查平移的意义.
26.小红语文、数学、英语三门功课的平均分是94分,她语文得了90分,数学和英语得了多少分?数学英语的平均分是多少分?
【分析】根据“平均成绩×科目的数量=总成绩”算出语文、数学、英语三门功课的总成绩,进而用“语文、数学、英语三门功课的总成绩分别减去语文功课的成绩,即可求出数学和英语得了多少分,再除以2即可.
【解答】解:94×3﹣90,
=282﹣90,
=192(分);
答:数学和英语得了192分.
192÷2=96(分);
答:数学英语的平均分是96分.
【点评】解答此题的关键是:先根据平均数的计算方法求出三门课程的总成绩,然后分别减去语文的成绩,进而解答即可.
27.植树节植树,学校买来樟树160棵,比杉树少28棵,把这些树平均分给12个班级种,每个班级要种多少棵?
【分析】由题意,先用加法求得植树的总棵数,用植树的总棵数除以总班数,就是平均每个班植的棵数,据此解答.
【解答】解:(160+28+160)÷12
=348÷12
=29(棵)
答:平均每个班要种29棵.
【点评】本题依据除法平均分的意义列式求解即可
第1页(共1页)
同课章节目录
