矩形 课件
图片预览




文档简介
课件26张PPT。人教版数学教材八年级下19.2特殊的平行四边形19.2.1矩形的判定一起放飞理想的翅膀在知识的天空中自由翱翔矩形有而平行四边形没有的性质是 .
①对角相等; ②对角线相等;
③对角线互相平分; ④对边平行且相等;
⑤轴对称图形; ⑥邻角互补;
⑦邻角相等; ⑧邻边垂直;
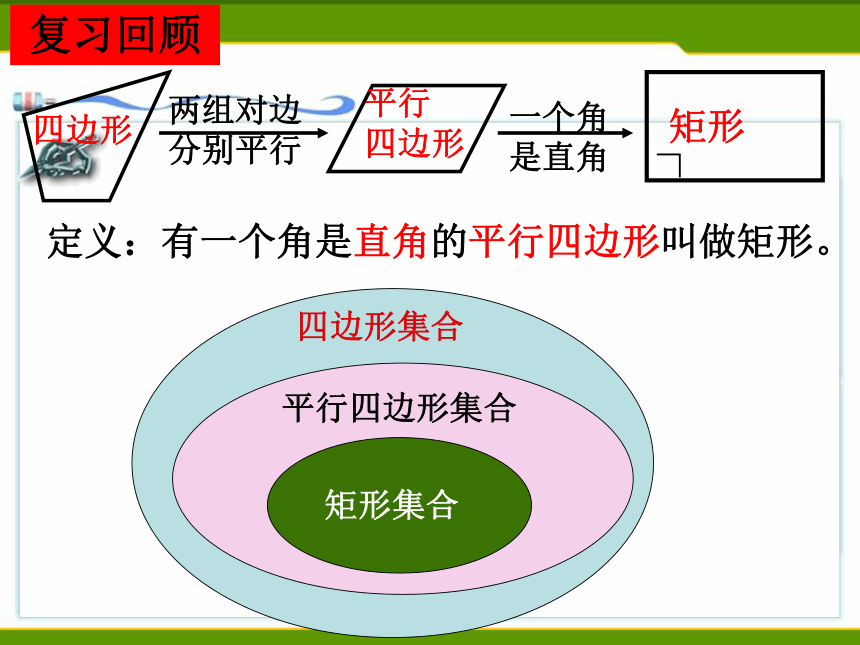
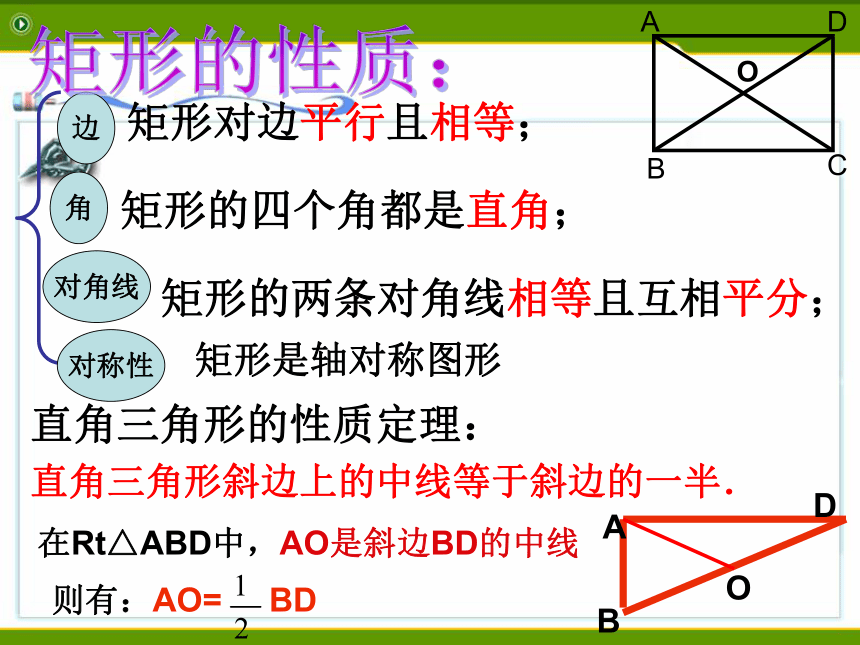
⑨有一个直角; ⑩四个角都相等.回顾与思考:复习回顾四边形定义:有一个角是直角的平行四边形叫做矩形。边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的两条对角线相等且互相平分;直角三角形斜边上的中线等于斜边的一半. 在Rt△ABD中,AO是斜边BD的中线则有:AO= BD直角三角形的性质定理:对称性矩形是轴对称图形直角三角形斜边上的中线等于斜边一半B具体事例2.长4m的竹竿贴墙而立(AB),竹竿底部
往外滑动,倒在地上(BC),则竹竿中点O的运动轨
迹是什么?运动路线有多长?AB斜边上有中点的时候,
应立即连接直角顶点.方法一.
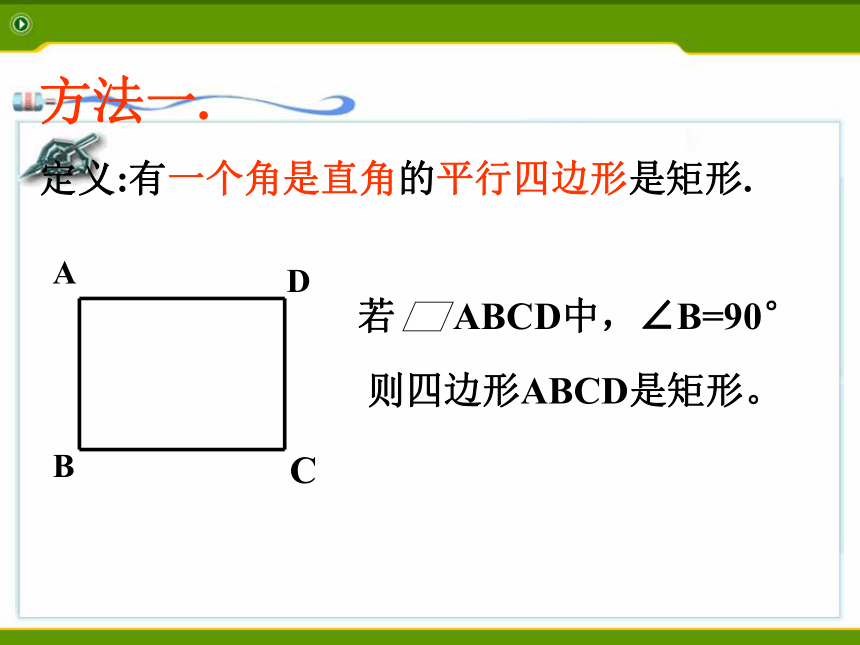
定义:有一个角是直角的平行四边形是矩形.AB CD若 ABCD中,∠B=90° 则四边形ABCD是矩形。有一个角是直角
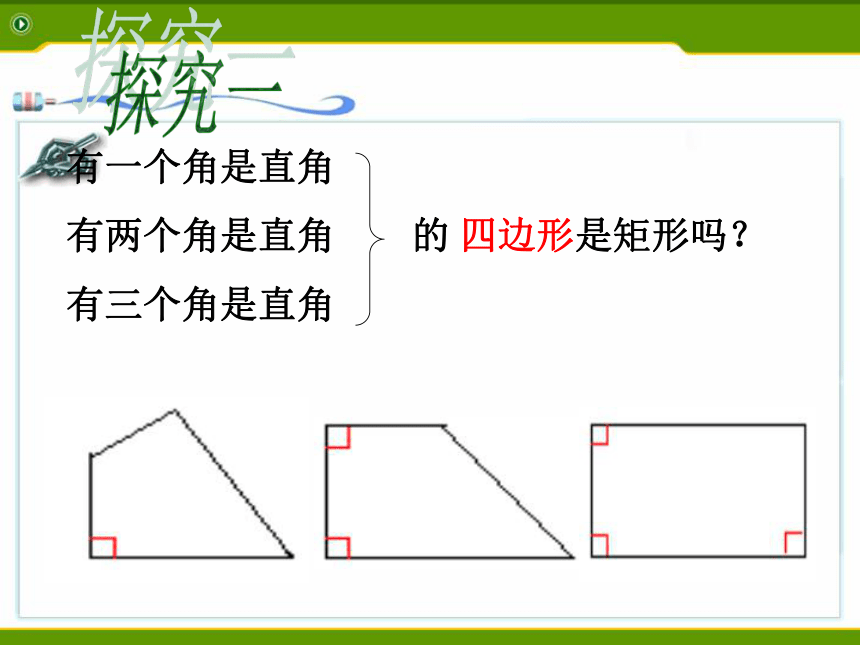
有两个角是直角 的 四边形是矩形吗?
有三个角是直角
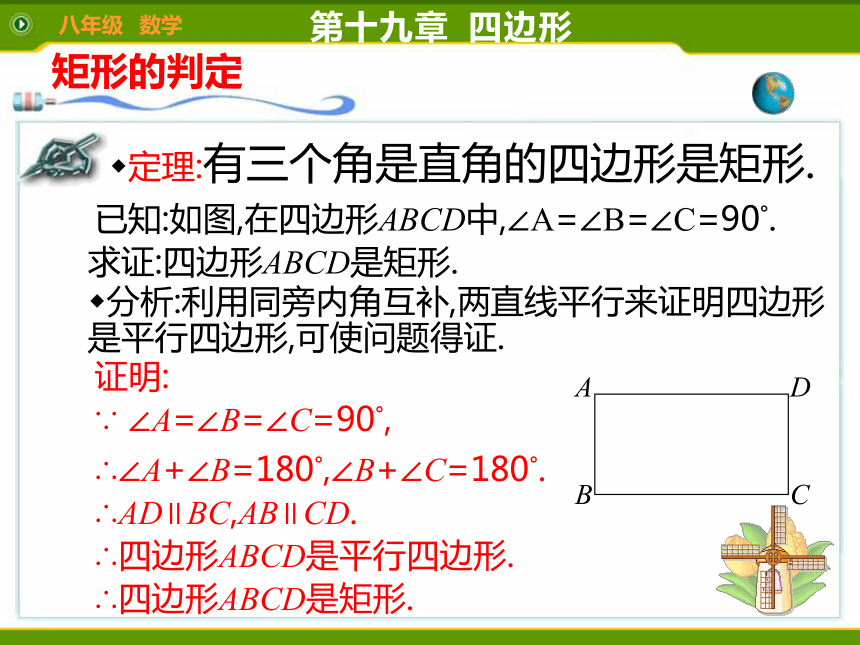
探究一矩形的判定定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.八年级 数学第十九章 四边形方法二
有三个角是直角的四边形是矩形.若∠A=∠B=∠C=90°则四边形ABCD是矩形探究二方法三
对角线相等的平行四边形是矩形.若 ABCD中, AC=BD则四边形ABCD是矩形1.一个角是直角的平行四边形是矩形。
2.三个角是直角是四边形是矩形。
3.对角线相等的平行四边形是矩形。
归纳:矩形的三种判定方法方法指导:联系实际:工人师傅在做门框时,
不仅要测量两组对边是否相等,
还要测量对角线是否相等,这是
为什么呢?①有一个直角②对角线相等有3个直角的四边形是矩形对角线互
相平分对角线互相平分且相等的四边形是矩形平行四边形动手探究 李芳同学用画“边-直角、边-直角、边-直角、边”这样四步画出一个四边形,她说这就是一个矩形,她的判断对吗?你能证明吗?②①③④八年级 数学第十九章 四边形例1:如图,△ABC中,AB=AC,延长BA到D,使AD=AB,
延长CA到E,使AE=AC,连结CD,DE,EB.
求证:四边形BCDE是矩形.①先判定平行四边形;②再寻找一个条件.范例解析,当堂练习证明:∵AD=AB,AE=AC又∵AB=AC∴CE=BD∴矩形BCDE练一练:为庆祝五一国际劳动节,初二(3)(4)两
班同学要在校前广场布置一个矩形花坛,计划
用红花均匀摆成两条对角线,若一条对角线用
了38盆红花,这时应从花房中再搬多少盆红花?
若一条对角线用了49盆红花呢?为什么?范例解析,当堂练习1. 的平行四边形是矩形.对角线 的平行四边形是矩形.有三个角是直角的四边形是 形。
2.如图,工人师傅做铝合金窗框分下面几个步骤进行:
(1)先截出两对符合规格的铝合金窗(如图①)使AB=CD、 EF=GH; (2)摆放成(如图②)的四边形,则这时窗框的形状是 ,根据的数学道理是 。
(3)将直角尺靠紧窗框的一个角(如图③)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格这时窗框是 ,根据的数学道理是 。
二、基础巩固3、下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的
四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX1、已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是______;
(2)试用理由说明你的猜想.三、牛刀小试例3:如图,△ABC中,点O是AC边上一个动点,过点O作直线a∥BC,设a交∠ACB的平分线于点E, 交∠ACB的外角平分线于点F.
(1)求证:CE⊥CF;
(2)求证:EO=FO;
(3)当点O运动到何处时,
四边形AECF是矩形.ABCDOEF231a456范例解析,当堂练习自我诊断 1、能够判断一个四边形是矩形的条件是( )
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定八年级 数学第十九章 四边形 1、如图,矩形ABCD的对角线AC、BD相交于O,∠BOC=2 ∠ AOB,若AC=6cm,试求AB的长.
2、如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.八年级 数学随堂练第十九章 四边形已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
(1).求证:AP⊥PB;
(2).如果AD=5cm,AP=8cm,那么AB的长是多少? △APB的面积是多少?八年级 数学随堂练第十九章 四边形学习了本节课你有何收获? 1. P105 练习,
2. P112-114,
1、2、3、4、14作业
①对角相等; ②对角线相等;
③对角线互相平分; ④对边平行且相等;
⑤轴对称图形; ⑥邻角互补;
⑦邻角相等; ⑧邻边垂直;
⑨有一个直角; ⑩四个角都相等.回顾与思考:复习回顾四边形定义:有一个角是直角的平行四边形叫做矩形。边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的两条对角线相等且互相平分;直角三角形斜边上的中线等于斜边的一半. 在Rt△ABD中,AO是斜边BD的中线则有:AO= BD直角三角形的性质定理:对称性矩形是轴对称图形直角三角形斜边上的中线等于斜边一半B具体事例2.长4m的竹竿贴墙而立(AB),竹竿底部
往外滑动,倒在地上(BC),则竹竿中点O的运动轨
迹是什么?运动路线有多长?AB斜边上有中点的时候,
应立即连接直角顶点.方法一.
定义:有一个角是直角的平行四边形是矩形.AB CD若 ABCD中,∠B=90° 则四边形ABCD是矩形。有一个角是直角
有两个角是直角 的 四边形是矩形吗?
有三个角是直角
探究一矩形的判定定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.八年级 数学第十九章 四边形方法二
有三个角是直角的四边形是矩形.若∠A=∠B=∠C=90°则四边形ABCD是矩形探究二方法三
对角线相等的平行四边形是矩形.若 ABCD中, AC=BD则四边形ABCD是矩形1.一个角是直角的平行四边形是矩形。
2.三个角是直角是四边形是矩形。
3.对角线相等的平行四边形是矩形。
归纳:矩形的三种判定方法方法指导:联系实际:工人师傅在做门框时,
不仅要测量两组对边是否相等,
还要测量对角线是否相等,这是
为什么呢?①有一个直角②对角线相等有3个直角的四边形是矩形对角线互
相平分对角线互相平分且相等的四边形是矩形平行四边形动手探究 李芳同学用画“边-直角、边-直角、边-直角、边”这样四步画出一个四边形,她说这就是一个矩形,她的判断对吗?你能证明吗?②①③④八年级 数学第十九章 四边形例1:如图,△ABC中,AB=AC,延长BA到D,使AD=AB,
延长CA到E,使AE=AC,连结CD,DE,EB.
求证:四边形BCDE是矩形.①先判定平行四边形;②再寻找一个条件.范例解析,当堂练习证明:∵AD=AB,AE=AC又∵AB=AC∴CE=BD∴矩形BCDE练一练:为庆祝五一国际劳动节,初二(3)(4)两
班同学要在校前广场布置一个矩形花坛,计划
用红花均匀摆成两条对角线,若一条对角线用
了38盆红花,这时应从花房中再搬多少盆红花?
若一条对角线用了49盆红花呢?为什么?范例解析,当堂练习1. 的平行四边形是矩形.对角线 的平行四边形是矩形.有三个角是直角的四边形是 形。
2.如图,工人师傅做铝合金窗框分下面几个步骤进行:
(1)先截出两对符合规格的铝合金窗(如图①)使AB=CD、 EF=GH; (2)摆放成(如图②)的四边形,则这时窗框的形状是 ,根据的数学道理是 。
(3)将直角尺靠紧窗框的一个角(如图③)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格这时窗框是 ,根据的数学道理是 。
二、基础巩固3、下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的
四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX1、已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是______;
(2)试用理由说明你的猜想.三、牛刀小试例3:如图,△ABC中,点O是AC边上一个动点,过点O作直线a∥BC,设a交∠ACB的平分线于点E, 交∠ACB的外角平分线于点F.
(1)求证:CE⊥CF;
(2)求证:EO=FO;
(3)当点O运动到何处时,
四边形AECF是矩形.ABCDOEF231a456范例解析,当堂练习自我诊断 1、能够判断一个四边形是矩形的条件是( )
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定八年级 数学第十九章 四边形 1、如图,矩形ABCD的对角线AC、BD相交于O,∠BOC=2 ∠ AOB,若AC=6cm,试求AB的长.
2、如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.八年级 数学随堂练第十九章 四边形已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
(1).求证:AP⊥PB;
(2).如果AD=5cm,AP=8cm,那么AB的长是多少? △APB的面积是多少?八年级 数学随堂练第十九章 四边形学习了本节课你有何收获? 1. P105 练习,
2. P112-114,
1、2、3、4、14作业
