平行线的性质 课件

课件21张PPT。2.6 .平行线的性质新华中心学校七年级数学教研组 李锦凤想一想：若交换它们的已知和结论，即让两直线平行，会有什么结论呢？两条直线被第三条直线所截，
⑴若同位角相等，则两直线平行；
⑵若内错角相等，则两直线平行；
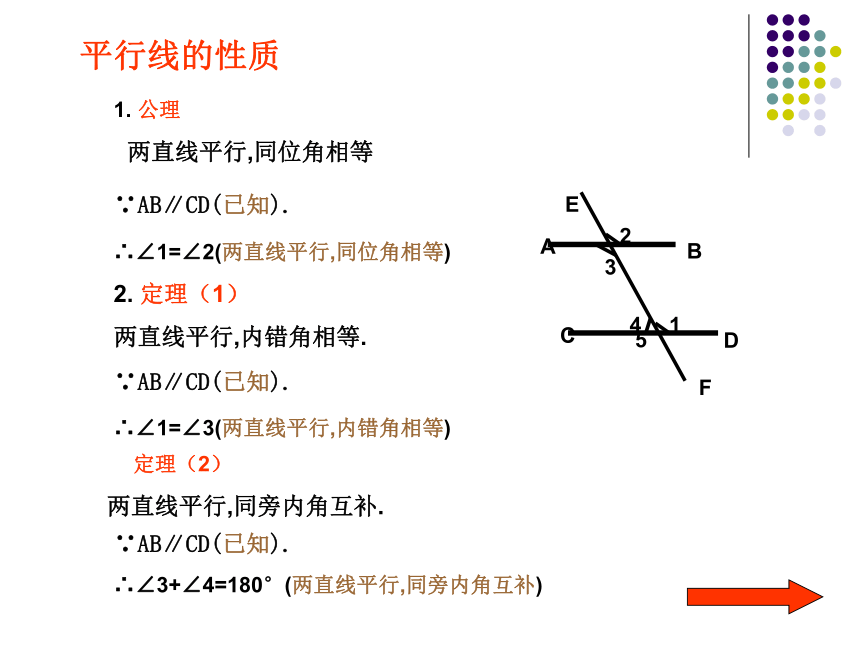
⑶若同旁内角互补，则两直线平行．ACBDa12 如果我们现在只知道“两直线平行,同位角相等”. 你能说明“两直线平行,内错角相等”, “两直线平行,同旁内角互补” 成立的理由吗? 请同学们仿照例子,把“两直线平行,同旁内角互补”的理由用符号语言写出来.平行线的性质 两直线平行,同位角相等 ∵AB∥CD(已知). 2. 定理（1）
两直线平行,内错角相等. 定理（2）
两直线平行,同旁内角互补.∵AB∥CD(已知).
∵AB∥CD(已知).
51. 公理∴∠1=∠2(两直线平行,同位角相等)∴∠1=∠3(两直线平行,内错角相等)
∴∠3+∠4=180°(两直线平行,同旁内角互补)
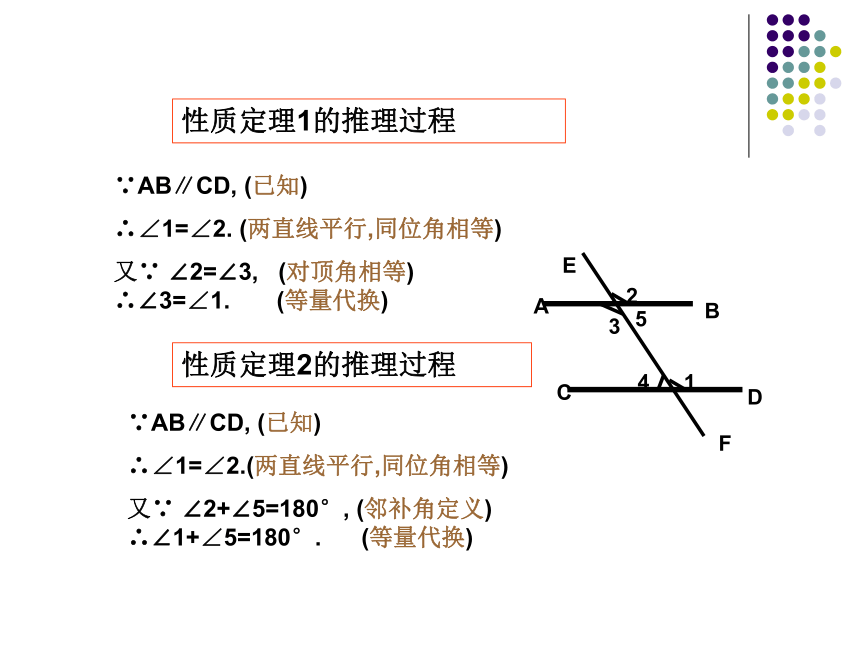
∵AB∥CD, (已知)
∴∠1=∠2. (两直线平行,同位角相等)
又∵ ∠2=∠3, (对顶角相等) ∴∠3=∠1. (等量代换)性质定理1的推理过程性质定理2的推理过程5∵AB∥CD, (已知)
∴∠1=∠2.(两直线平行,同位角相等)
又∵ ∠2+∠5=180°, (邻补角定义) ∴∠1+∠5=180°. (等量代换)结论 ?两直线平行，同位角相等
两直线平行，内错角相等
两直线平行，同旁内角互补例1 ： 如图是梯形有上底的一部分。已经量得∠A=115°，∠D=100°，梯形另外两个角分别是多少？
AD解：∵梯形的上下底AD∥BC（已知）
∴∠A+∠B=180°，
∠D+∠C=180°（两直线平 行，同旁内角互补）
∴∠ B=180°-115°=65°
∠ C=180°-100°=80°
答：梯形的另外的两个角分别是65°、 80 ° .练习1：（抢答）判断题：（判断对错并说明理由.）1、两直线被第三条直线所截，同位角相等2、两直线平行，同旁内角相等3、“内错角相等，两直线平行”是平行线的性质4、“两直线平行，同旁内角互补”是平行线的性质练习2：（抢答）ABDCE1234（2）从∠ 1=110 °可以知道∠ 3是多少度？为什么？（3）从∠ 1=110 °可以知道∠ 4是多少度？为什么？（1）从∠1=110°可以知道∠ 2是多少度？为什么？ 如图，已知AB∥CD，被直线AE所截.
理由：∵AB∥CD（已知）
∴∠2= ∠ 1=110（两直线平行，内错角相等）解： ∠3= 110°
理由：∵AB∥CD（已知）
∴∠3= ∠ 1=110°（两直线平行，同位角相等）解： ∠4 =70°
理由：∵AB∥CD（已知）
∴∠4+ ∠ 1=180°（两直线平行，同旁内角互补） ∴ ∠4 =180 °- 110°=70°解： ∠2= 110°
BCADE练习3：（抢答）
如图，已知D是AB上一点，E是AC上一点， ∠ADE=60°，∠B=60°，∠AED=40°.（1）DE、BC平行吗？为什么？（2）∠C等于多少度？为什么？ （1）∵∠ADE= ∠B=60° ， （已知）
∴DE∥BC（同位角相等，两直线平行）BCDEA（2）∵ DE∥BC （由上题知）
∴∠C= ∠AED=40° ， （两直线平行，同位角相等）答案练习4：选择题
如图，AB∥DE，B C∥EF，则下列选项正确的是（ ） ABCDEF123A. ∠B= ∠ 1.理由是内错角相等，两直线平行.D . ∠ E= ∠ 3.理由是两直线平行，同位
角相等.B. ∠ B+ ∠ 2=180.理由是，两直线平行， 同
旁内角相等.C .∠ B= ∠ E.理由是两直线平行，同位
角相等.D例:解:∵AD∥BC(已知)
∴∠C=∠CDE(两直线平行,内错角相等)
又∵ ∠A=∠C(已知)
∴ ∠A=∠CDE(等量代换)
∴AB∥DC(同位角相等,两直线平行)A小明在纸上画了一个角∠A，准备去测量它的度数，因不小心将纸片撕破，只省下如图的一部分，如果不能延长DC、FE的话，你能帮他设计出多少种方法可以测出∠A的度数？A小明在纸上画了一个角A，准备去测量它的度数，因不小心将纸片撕破，只省下如图的一部分，如果不能延长DC、FE的话，你能帮他设计出多少种方法可以测出A的度数？A小明在纸上画了一个角A，准备去测量它的度数，因不小心将纸片撕破，只省下如图的一部分，如果不能延长DC、FE的话，你能帮他设计出多少种方法可以测出A的度数？同位角相等内错角相等同旁内角互补两直线平行同位角相等内错角相等同旁内角互补判定
性质 （数量关系）（位置关系）（数量关系）平行线的判定与性质的关系图课外探究活动 小红学了这一节课后，他了解到两平行线被第三条直线所截构成的同旁内角之和等于180度后，他开动脑筋，大胆猜想：如果两直线不平行时，无论截线怎么画，构成的同旁内角之和虽不等于180度，但它们的和会不会具有一定规律呢？于是他经过反复的测量，令其兴奋的是：发现一个规律.你猜猜看他发现了什么呢？请你用所学知识解释.