湘教版数学七年级下册 章末复习 课件(共22张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 章末复习 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 17:24:52 | ||
图片预览






文档简介
(共23张PPT)
章末复习
湘教版 七年级下册
知识结构图:
相交线与平行线
相交线
平行线
补角、余角、对顶角
丰富情景
探索直线平行的特征
探索直线平行的条件
同位角
内错角
同旁内角
复习旧知
概念、性质填空:
一、概念:
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。
二、性质:
_________的余角相等;
同角或等角的____相等;
对顶角_____。
直角
补角
对顶角
同角或等角
补角
相等
余角、补角
1、已知一个角为50度,则它的余角为___度,补角为____度。
小结:求余角、补角的方法:
①求一个角的余角,就用90°去减这个角。
②求一个角的余角,就用180°去减这个角。
40
130
知识应用
2. 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是_____________。
2
1
3
C
=
同角的余角相等
对顶角
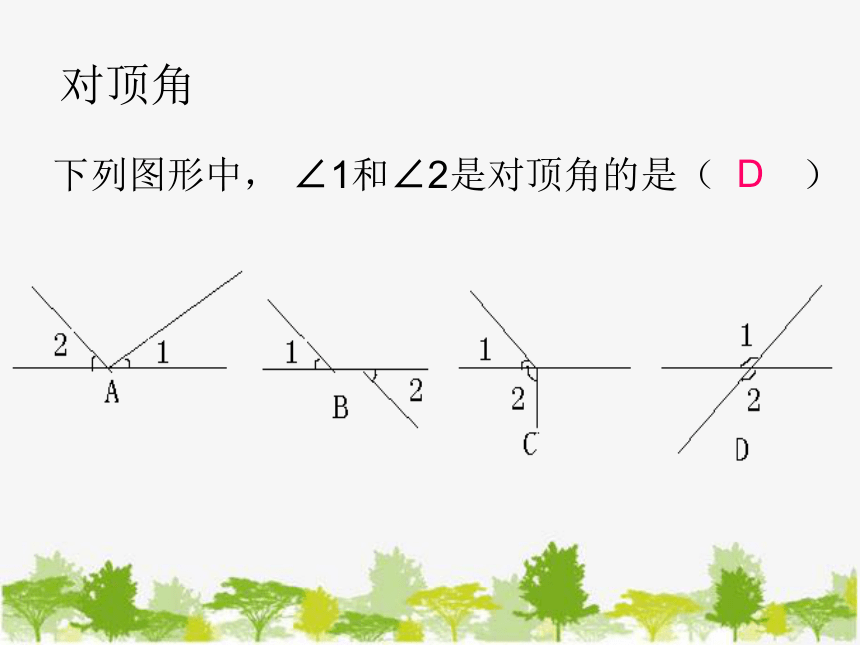
下列图形中, ∠1和∠2是对顶角的是( )
D
对顶角
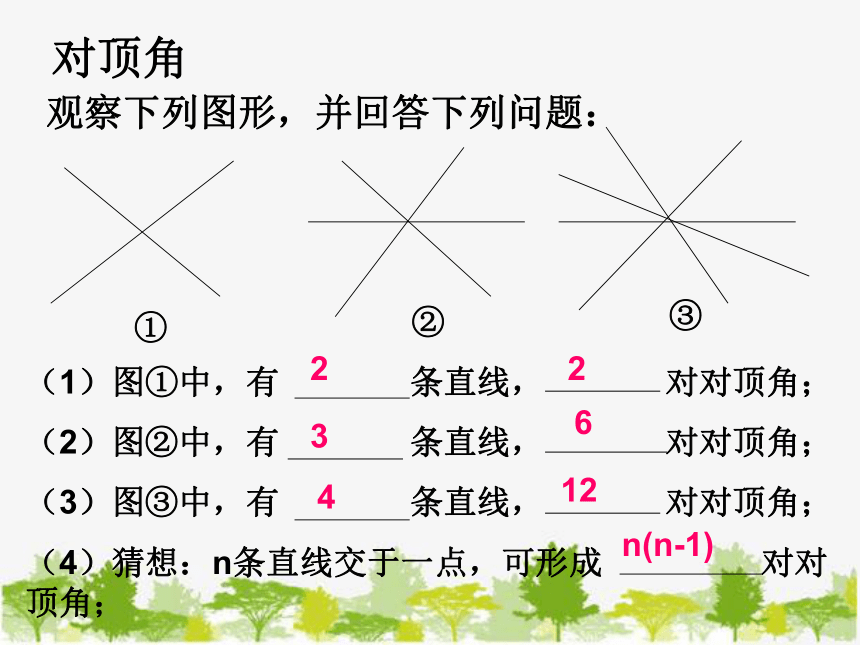
观察下列图形,并回答下列问题:
(1)图①中,有 条直线, 对对顶角;
(2)图②中,有 条直线, 对对顶角;
(3)图③中,有 条直线, 对对顶角;
(4)猜想:n条直线交于一点,可形成 对对顶角;
①
②
③
2
3
4
2
6
12
n(n-1)
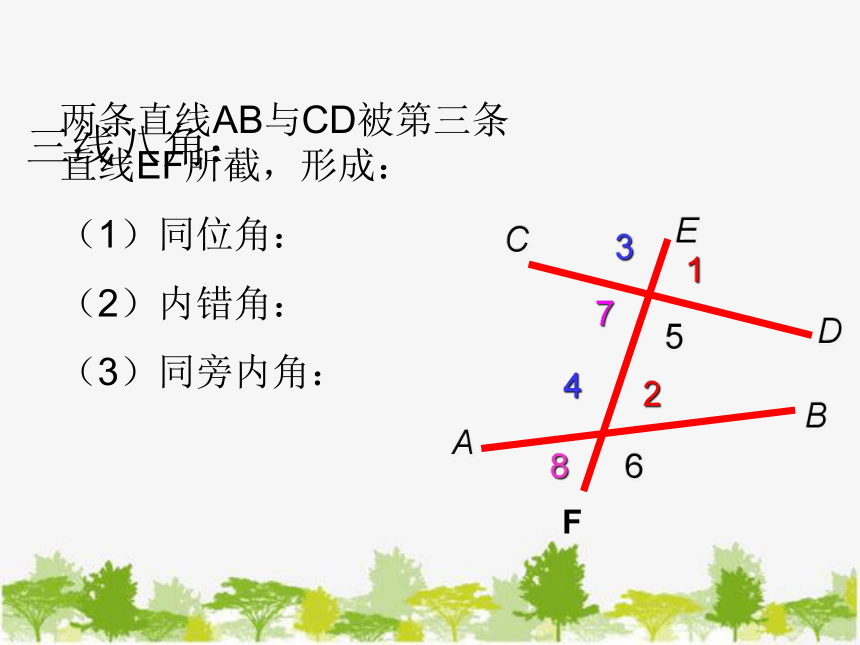
三线八角:
两条直线AB与CD被第三条直线EF所截,形成:
(1)同位角:
(2)内错角:
(3)同旁内角:
C
A
1
3
7
5
2
8
6
E
4
D
B
F
区别:条件与结论互换,
即:已知平行用特征,证明平行用判定。
一、平行线的判定方法:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
二、平行线的特征:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
a
b
在下面的两幅图中,直线a与直线b平行吗?试着说明你的理由。
45°
135°
110°
70°
考察知识点:平行线的判定
3种判定方法:①同位角相等 ②内错角相等 ③同旁内角互补
三种方法只要其中之一符合即可判定两直线平行
在下列各图中,a //b,分别计算∠1的度数。
36°
120°
考察知识点:平行线的特征
①同位角相等 ②内错角相等 ③同旁内角互补
注:已知两直线平行,则三个特征同时成立。
1.(1)若∠1=50 °,
则∠2 =_______
∠BOC=_______。
O
A
B
C
D
2
1
(2)若∠BOC=2∠1,
则∠1=______
∠BOC=_______。
(3)若OE⊥AB ,∠1=56°,
则∠3=_____。
60°
120 °
34°
50°
130°
3
E
课堂演练
2、将一等腰直角三角板与两边平行的纸条如图所示放置,下面结论:(1)∠1= ∠2;(2) ∠3= ∠4;(3)∠2+ ∠4= 90°;(4) ∠4+ ∠5= 180 °,其中正确的个数是( )
A、1 B、2 C、3 D、4
1
2
3
4
5
1
1
D
考察知识点:
两直线平行的特征
3、如图,已知AB //CD,直线l分别交AB 、CD于点E、F,EG平分∠BEF,若∠EFG = 40°,则∠EGF 的度数是( )
A、 70° B、 60° C、 80° D 、90°
A
B
C
D
E
F
G
l
A
考察知识点:
两直线平行的特征
4、已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°
求证:AB//CD (在括号中填写下列理由)
A
B
C
D
E
F
1
2
H
G
证明:
∵∠1+∠3=180°( )
∠1+∠2=180°( )
3
考察知识点:平行线的判定
∴ ∠3=∠2 ( )
∴AB//CD( )
平角的定义
已知
同角的补角相等
同位角相等,两直线平行
5.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程)
A
D
B
C
115°
110°
解:∵AD∥BC (已知)
∴∠A+ ∠B=180 °
∠D+ ∠C=180 °
(两直线平行,同旁内角互补)
又∵ ∠A=115°, ∠D=110°(已知)
∴∠B=180°﹣115°=65 °
∠C=180°-110°=70 °
证明:∵BD平分∠ABC( )
∴∠2=∠3( )
又∵∠2=∠1( )
∴∠3= ∠1( )
∴AD∥BC
( )
6.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC.
A
B
C
D
1
2
3
已知
角平分线定义
已知
等量代换
内错角相等,两直线平行
7.如图已知∠1=∠ACB, ∠2=∠3.
求证:CD∥FH.
(小明写了相关的过程,但是却忘了写理由
请你帮他把理由补充完整)
解:∵ ∠1=∠ACB(已知)
∴DE∥BC( )
∴ ∠2 =∠DCF( )
又∵ ∠2=∠3(已知)
∴ ∠3 =∠DCF( )
∴ CD∥FH( )
H
A
C
B
F
D
E
1
2
3
同位角相等,两直线平行
两直线平行,内错角相等
等量代换
同位角相等,两直线平行
8.如图已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系?说说你的理由。
(2)你能说明∠1+∠2=180°吗?
A
D
C
B
1
2
4
3
解:(1)∵ DC⊥AD于D(已知)
∴∠3=90°(垂直定义)
又∵ AD∥BC(已知)
∴∠3+∠DCB=180°
(两直线平行,同旁内角互补)
∴ ∠DCB=180°-90°=90°
因此 , DC⊥BC
A
D
C
B
1
2
4
3
(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
章末复习
湘教版 七年级下册
知识结构图:
相交线与平行线
相交线
平行线
补角、余角、对顶角
丰富情景
探索直线平行的特征
探索直线平行的条件
同位角
内错角
同旁内角
复习旧知
概念、性质填空:
一、概念:
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。
二、性质:
_________的余角相等;
同角或等角的____相等;
对顶角_____。
直角
补角
对顶角
同角或等角
补角
相等
余角、补角
1、已知一个角为50度,则它的余角为___度,补角为____度。
小结:求余角、补角的方法:
①求一个角的余角,就用90°去减这个角。
②求一个角的余角,就用180°去减这个角。
40
130
知识应用
2. 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是_____________。
2
1
3
C
=
同角的余角相等
对顶角
下列图形中, ∠1和∠2是对顶角的是( )
D
对顶角
观察下列图形,并回答下列问题:
(1)图①中,有 条直线, 对对顶角;
(2)图②中,有 条直线, 对对顶角;
(3)图③中,有 条直线, 对对顶角;
(4)猜想:n条直线交于一点,可形成 对对顶角;
①
②
③
2
3
4
2
6
12
n(n-1)
三线八角:
两条直线AB与CD被第三条直线EF所截,形成:
(1)同位角:
(2)内错角:
(3)同旁内角:
C
A
1
3
7
5
2
8
6
E
4
D
B
F
区别:条件与结论互换,
即:已知平行用特征,证明平行用判定。
一、平行线的判定方法:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
二、平行线的特征:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
a
b
在下面的两幅图中,直线a与直线b平行吗?试着说明你的理由。
45°
135°
110°
70°
考察知识点:平行线的判定
3种判定方法:①同位角相等 ②内错角相等 ③同旁内角互补
三种方法只要其中之一符合即可判定两直线平行
在下列各图中,a //b,分别计算∠1的度数。
36°
120°
考察知识点:平行线的特征
①同位角相等 ②内错角相等 ③同旁内角互补
注:已知两直线平行,则三个特征同时成立。
1.(1)若∠1=50 °,
则∠2 =_______
∠BOC=_______。
O
A
B
C
D
2
1
(2)若∠BOC=2∠1,
则∠1=______
∠BOC=_______。
(3)若OE⊥AB ,∠1=56°,
则∠3=_____。
60°
120 °
34°
50°
130°
3
E
课堂演练
2、将一等腰直角三角板与两边平行的纸条如图所示放置,下面结论:(1)∠1= ∠2;(2) ∠3= ∠4;(3)∠2+ ∠4= 90°;(4) ∠4+ ∠5= 180 °,其中正确的个数是( )
A、1 B、2 C、3 D、4
1
2
3
4
5
1
1
D
考察知识点:
两直线平行的特征
3、如图,已知AB //CD,直线l分别交AB 、CD于点E、F,EG平分∠BEF,若∠EFG = 40°,则∠EGF 的度数是( )
A、 70° B、 60° C、 80° D 、90°
A
B
C
D
E
F
G
l
A
考察知识点:
两直线平行的特征
4、已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°
求证:AB//CD (在括号中填写下列理由)
A
B
C
D
E
F
1
2
H
G
证明:
∵∠1+∠3=180°( )
∠1+∠2=180°( )
3
考察知识点:平行线的判定
∴ ∠3=∠2 ( )
∴AB//CD( )
平角的定义
已知
同角的补角相等
同位角相等,两直线平行
5.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程)
A
D
B
C
115°
110°
解:∵AD∥BC (已知)
∴∠A+ ∠B=180 °
∠D+ ∠C=180 °
(两直线平行,同旁内角互补)
又∵ ∠A=115°, ∠D=110°(已知)
∴∠B=180°﹣115°=65 °
∠C=180°-110°=70 °
证明:∵BD平分∠ABC( )
∴∠2=∠3( )
又∵∠2=∠1( )
∴∠3= ∠1( )
∴AD∥BC
( )
6.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC.
A
B
C
D
1
2
3
已知
角平分线定义
已知
等量代换
内错角相等,两直线平行
7.如图已知∠1=∠ACB, ∠2=∠3.
求证:CD∥FH.
(小明写了相关的过程,但是却忘了写理由
请你帮他把理由补充完整)
解:∵ ∠1=∠ACB(已知)
∴DE∥BC( )
∴ ∠2 =∠DCF( )
又∵ ∠2=∠3(已知)
∴ ∠3 =∠DCF( )
∴ CD∥FH( )
H
A
C
B
F
D
E
1
2
3
同位角相等,两直线平行
两直线平行,内错角相等
等量代换
同位角相等,两直线平行
8.如图已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系?说说你的理由。
(2)你能说明∠1+∠2=180°吗?
A
D
C
B
1
2
4
3
解:(1)∵ DC⊥AD于D(已知)
∴∠3=90°(垂直定义)
又∵ AD∥BC(已知)
∴∠3+∠DCB=180°
(两直线平行,同旁内角互补)
∴ ∠DCB=180°-90°=90°
因此 , DC⊥BC
A
D
C
B
1
2
4
3
(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
