华东师大版数学七年级下册 9.1.2 三角形的内角和与外角和 课件 (共25张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册 9.1.2 三角形的内角和与外角和 课件 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 05:59:43 | ||
图片预览






文档简介
(共25张PPT)
泰
名师点拨
重难点解读
1.三角形内角和定理的推
导可以用几种方法得到.由此推
导过程,让学生体会转化的思想
方法,要会利用定理进行计算.
2.注意一个外角一定是大于
任何一个与它不相邻的内角,会利
用这个定理证明角的不等关系。
方法技巧
1.三角形内角和定理
的
“四个应用”
(1)在三角形中已知两个内角
的度数,求第三个内角的度数
(2)在三角形中已知一个
内角的度数,求另两个内角的度
数和.
(3)在三角形中已知三个
内角的度数关系,求这三个内角
的度数.
(4)根据三角形的内角和
判断一个三角形至少有几个锐
角,最多有几个钝角或直角
2.运用三角形外角性质解
决问题时的两点注意
(1)明确要求的角或已知
的角是哪个三角形的外角.
(2)由三角形内角与外角
的性质进行计算.
易错易混
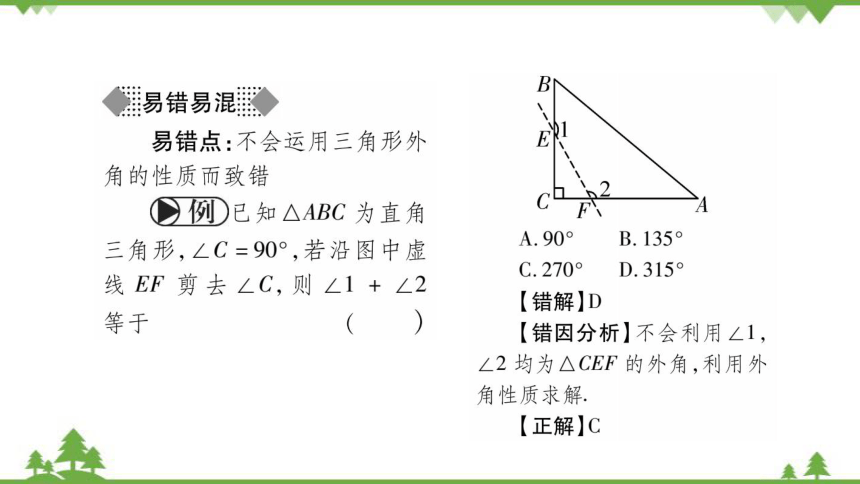
易错点:不会运用三角形外
角的性质而致错
C例)已知△ABC为直角
三角形,∠C=90°,若沿图中虚
线EF剪去∠C,则∠1+∠2
等于
(
B
2
A
A.90°
B.135
C.270°
D.315
【错解】D
【错因分析】不会利用∠1,
∠2均为△CEF的外角,利用外
角性质求解.
【正解】C
曾基础训练孝无隆:女华
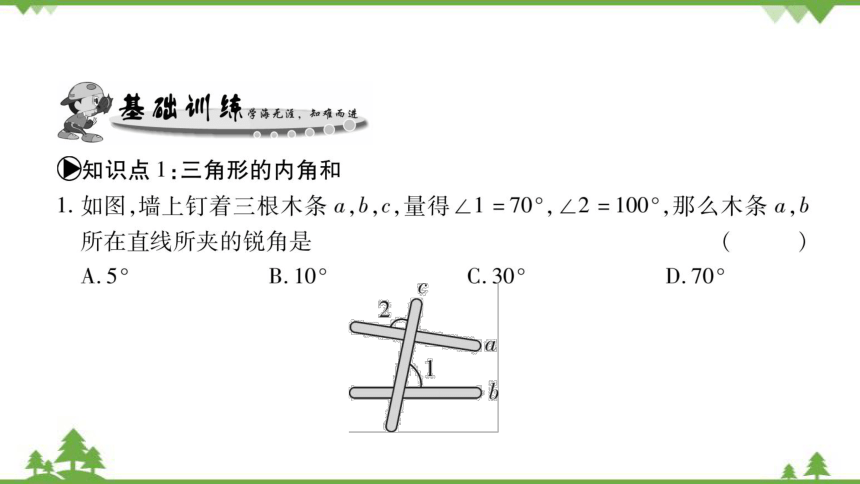
○知识点1:三角形的内角和
1.如图,墙上钉着三根木条a,b,c,量得∠1=70°,∠2=100°,那么木条a,b
所在直线所夹的锐角是
(B)
A.5
B.10°
C.30
D.70°
3.在△ABC中,2(∠B+∠C)=4∠A,则∠A的度数是60°
4.在△ABC中,∠B-∠A=70°,∠B=2∠C,求∠A,∠B,∠C的度数
解:∠B-∠A=70°,∠B=2∠C,
.∴.∠A=∠B-70°=2∠C-70°,
.∠A+∠B+∠C=180°,
.∴.2∠C-70°+2∠C+∠C=180°,
∴.∠C=50°,.∠A=30°,∠B=100°.
8.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC
于点E.若∠A=54°,∠B=48°,求∠CDE的度数,
解:∠A=54°,∠B=48°,
∴.∠ACB=180°-∠A-∠B=78°.
.CD平分∠ACB,∴.∠ACD=∠BCD=39°.
D
E
.DE∥BC,∴.∠CDE=∠BCD=39°.
B
c
能力训练
学致用,能力提升
9.如图,直线a,b,c,d互不平行,对它们截出的一些角
的数量关系描述错误的是
(D)
A.∠1+∠4+∠5=180°
B.∠4+∠5=∠2
C.∠1+∠3+∠6=180°
D.∠1+∠6=∠2
泰
名师点拨
重难点解读
1.三角形内角和定理的推
导可以用几种方法得到.由此推
导过程,让学生体会转化的思想
方法,要会利用定理进行计算.
2.注意一个外角一定是大于
任何一个与它不相邻的内角,会利
用这个定理证明角的不等关系。
方法技巧
1.三角形内角和定理
的
“四个应用”
(1)在三角形中已知两个内角
的度数,求第三个内角的度数
(2)在三角形中已知一个
内角的度数,求另两个内角的度
数和.
(3)在三角形中已知三个
内角的度数关系,求这三个内角
的度数.
(4)根据三角形的内角和
判断一个三角形至少有几个锐
角,最多有几个钝角或直角
2.运用三角形外角性质解
决问题时的两点注意
(1)明确要求的角或已知
的角是哪个三角形的外角.
(2)由三角形内角与外角
的性质进行计算.
易错易混
易错点:不会运用三角形外
角的性质而致错
C例)已知△ABC为直角
三角形,∠C=90°,若沿图中虚
线EF剪去∠C,则∠1+∠2
等于
(
B
2
A
A.90°
B.135
C.270°
D.315
【错解】D
【错因分析】不会利用∠1,
∠2均为△CEF的外角,利用外
角性质求解.
【正解】C
曾基础训练孝无隆:女华
○知识点1:三角形的内角和
1.如图,墙上钉着三根木条a,b,c,量得∠1=70°,∠2=100°,那么木条a,b
所在直线所夹的锐角是
(B)
A.5
B.10°
C.30
D.70°
3.在△ABC中,2(∠B+∠C)=4∠A,则∠A的度数是60°
4.在△ABC中,∠B-∠A=70°,∠B=2∠C,求∠A,∠B,∠C的度数
解:∠B-∠A=70°,∠B=2∠C,
.∴.∠A=∠B-70°=2∠C-70°,
.∠A+∠B+∠C=180°,
.∴.2∠C-70°+2∠C+∠C=180°,
∴.∠C=50°,.∠A=30°,∠B=100°.
8.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC
于点E.若∠A=54°,∠B=48°,求∠CDE的度数,
解:∠A=54°,∠B=48°,
∴.∠ACB=180°-∠A-∠B=78°.
.CD平分∠ACB,∴.∠ACD=∠BCD=39°.
D
E
.DE∥BC,∴.∠CDE=∠BCD=39°.
B
c
能力训练
学致用,能力提升
9.如图,直线a,b,c,d互不平行,对它们截出的一些角
的数量关系描述错误的是
(D)
A.∠1+∠4+∠5=180°
B.∠4+∠5=∠2
C.∠1+∠3+∠6=180°
D.∠1+∠6=∠2
