华东师大版数学七年级下册 10.5 图形的全等 课件(共24张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册 10.5 图形的全等 课件(共24张PPT) |

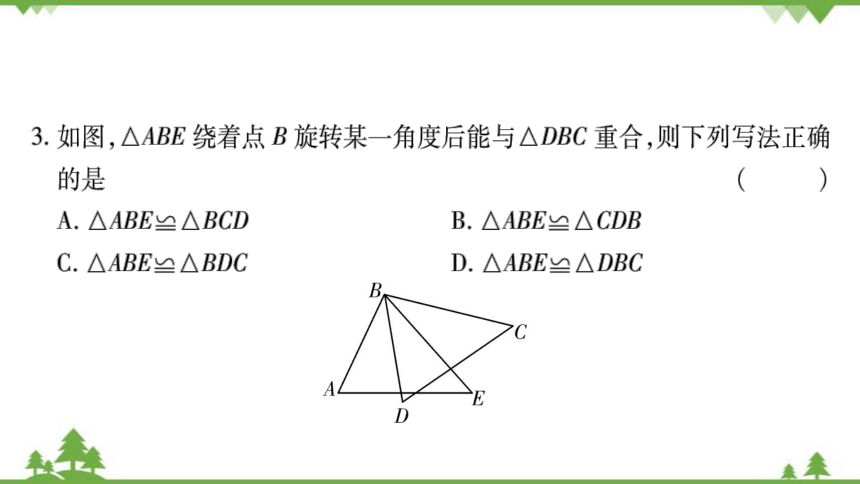
|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 06:06:14 | ||
图片预览




文档简介
(共24张PPT)
泰
名师点拨
重难点解读
1.经过平移、轴对称、旋转所
得的图形与原图形是全等图形.
2.应用全等图形的性质时,
要先确定哪两个图形全等,再找
对应顶点、对应边和对应角.
方法技巧
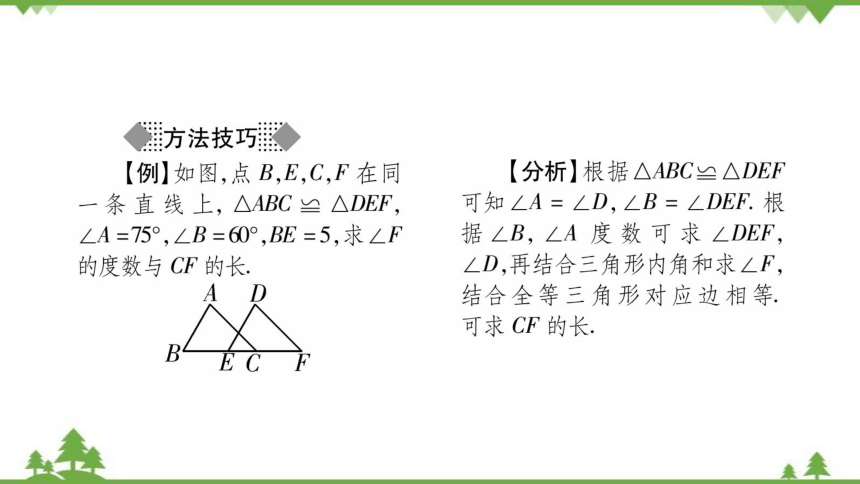
【例】如图,点B,E,C,F在同
一条直线上,△ABC≌△DEF,
∠A=75°,∠B=60°,BE=5,求∠F
的度数与CF的长.
B
【分析】根据△ABC≌△DEF
可知∠A=∠D,∠B=∠DEF.根
据∠B,∠A度数可求∠DEF,
∠D,再结合三角形内角和求∠F,
结合全等三角形对应边相等.
可求CF的长.
解:·△ABC≌△DEF,
.∴.∠F=∠ACB=180°-∠A-
∠B=180°-75°-60°=45°,
BC=EF...EF-EC=BC-EC,
即CF=BE=5.
在应用全等三角形的性质
时,根据需要选取对应边、对应
角,同时要结合三角形的内角和
进行计算.
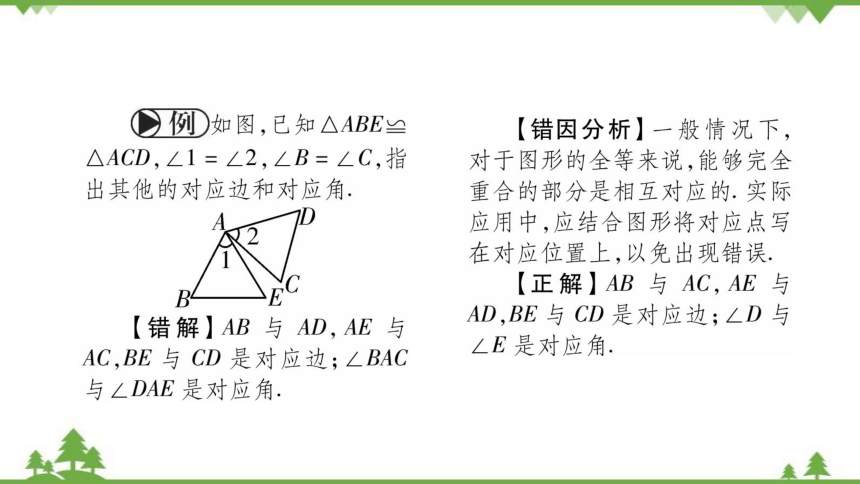
例)如图,已知△ABE兰
△ACD,∠1=∠2,∠B=∠C,指
出其他的对应边和对应角.
A
【错解】AB与AD,AE与
AC,BE与CD是对应边;∠BAC
与∠DAE是对应角.
【错因分析】一般情况下,
对于图形的全等来说,能够完全
重合的部分是相互对应的.实际
应用中,应结合图形将对应点写
在对应位置上,以免出现错误.
【正解】AB与AC,AE与
AD,BE与CD是对应边;∠D与
∠E是对应角
基础训练李降无该,知难而选
○知识点:全等图形的概念
1.下列说法正确的是
(C)
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
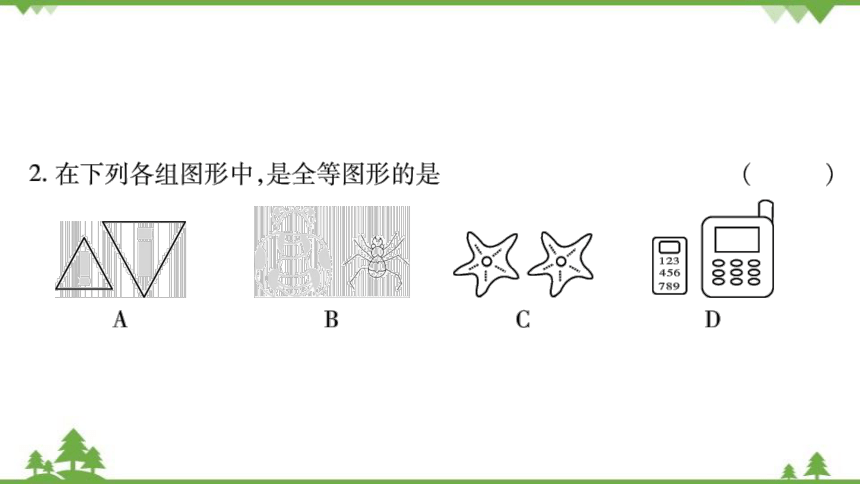
2.在下列各组图形中,是全等图形的是
C
倡游议斜
口
8
M
0
P
Q
7.如图,点E,C,F,B在同一条直线上,△ABC≌△DEF,∠A=25°,∠B=65°,
BF=2cm.求∠DFE的度数和EC的长.
解:∠DFE=0°,EC=2cm.
E
F
B
能力训练
学及致用,能力提升
8.下列说法正确的有
D
①大小相等、形状相同的两个图形是全等图形;②能
够完全重合的两个图形是全等形;③全等多边形的
对应边相等,对应角相等;④两个三角形的边、角分
别对应相等,这两个三角形全等
11.如图,在△ABC中,D,E分别是边BC,AC上的点,若
△EAB≌△EDB≌△EDC,则∠C的度数为(D)
A.15o
B.20°
C.25
D.30°
泰
名师点拨
重难点解读
1.经过平移、轴对称、旋转所
得的图形与原图形是全等图形.
2.应用全等图形的性质时,
要先确定哪两个图形全等,再找
对应顶点、对应边和对应角.
方法技巧
【例】如图,点B,E,C,F在同
一条直线上,△ABC≌△DEF,
∠A=75°,∠B=60°,BE=5,求∠F
的度数与CF的长.
B
【分析】根据△ABC≌△DEF
可知∠A=∠D,∠B=∠DEF.根
据∠B,∠A度数可求∠DEF,
∠D,再结合三角形内角和求∠F,
结合全等三角形对应边相等.
可求CF的长.
解:·△ABC≌△DEF,
.∴.∠F=∠ACB=180°-∠A-
∠B=180°-75°-60°=45°,
BC=EF...EF-EC=BC-EC,
即CF=BE=5.
在应用全等三角形的性质
时,根据需要选取对应边、对应
角,同时要结合三角形的内角和
进行计算.
例)如图,已知△ABE兰
△ACD,∠1=∠2,∠B=∠C,指
出其他的对应边和对应角.
A
【错解】AB与AD,AE与
AC,BE与CD是对应边;∠BAC
与∠DAE是对应角.
【错因分析】一般情况下,
对于图形的全等来说,能够完全
重合的部分是相互对应的.实际
应用中,应结合图形将对应点写
在对应位置上,以免出现错误.
【正解】AB与AC,AE与
AD,BE与CD是对应边;∠D与
∠E是对应角
基础训练李降无该,知难而选
○知识点:全等图形的概念
1.下列说法正确的是
(C)
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
2.在下列各组图形中,是全等图形的是
C
倡游议斜
口
8
M
0
P
Q
7.如图,点E,C,F,B在同一条直线上,△ABC≌△DEF,∠A=25°,∠B=65°,
BF=2cm.求∠DFE的度数和EC的长.
解:∠DFE=0°,EC=2cm.
E
F
B
能力训练
学及致用,能力提升
8.下列说法正确的有
D
①大小相等、形状相同的两个图形是全等图形;②能
够完全重合的两个图形是全等形;③全等多边形的
对应边相等,对应角相等;④两个三角形的边、角分
别对应相等,这两个三角形全等
11.如图,在△ABC中,D,E分别是边BC,AC上的点,若
△EAB≌△EDB≌△EDC,则∠C的度数为(D)
A.15o
B.20°
C.25
D.30°
