湘教版数学七年级下册 4.1.2 相交直线所成的角4课件(共11张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 4.1.2 相交直线所成的角4课件(共11张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 17:04:51 | ||
图片预览

文档简介
(共12张PPT)
湘教版 七年级下册
4.1.2 相交直线所成的角
D
C
B
A
O
1
2
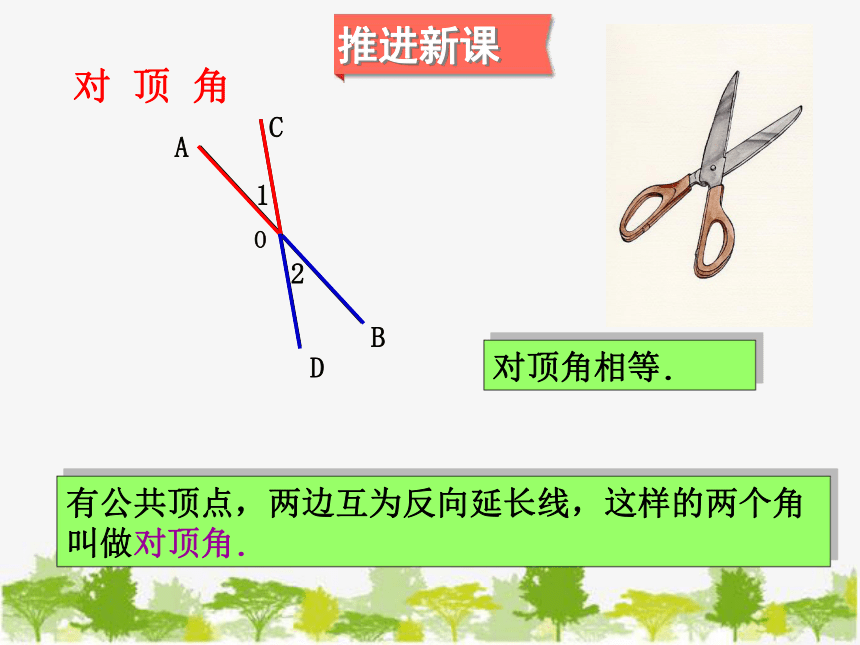
有公共顶点,两边互为反向延长线,这样的两个角 叫做对顶角.
对顶角相等.
对 顶 角
推进新课
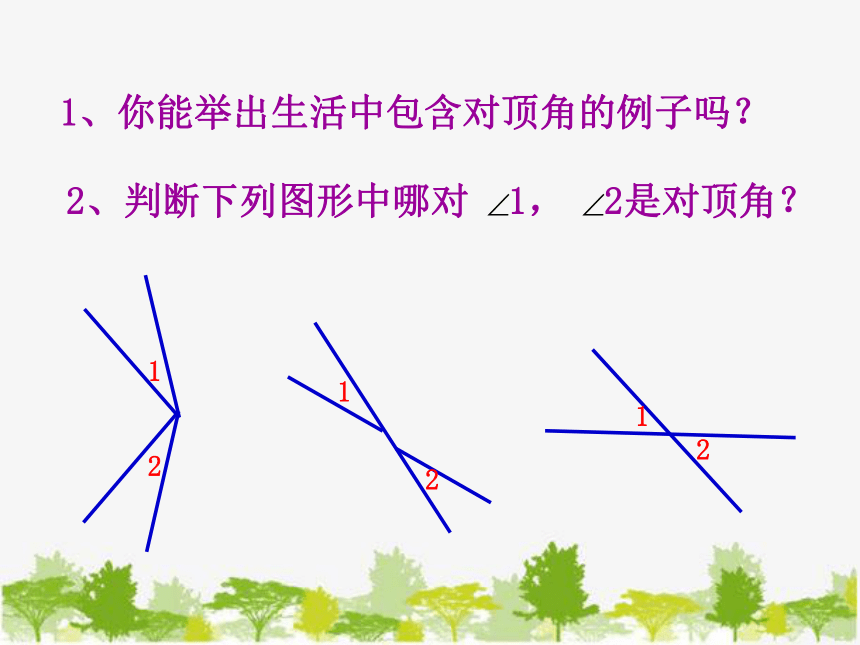
2、判断下列图形中哪对 1, 2是对顶角?
1
2
1
2
1
2
1、你能举出生活中包含对顶角的例子吗?
A
B
C
D
E
F
图四
2
3
6
7
8
4
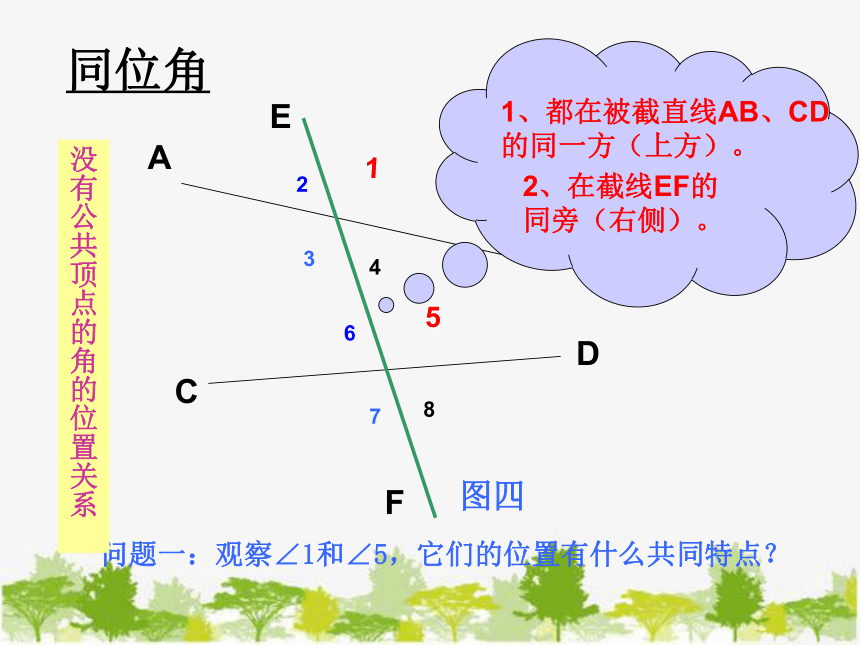
1、都在被截直线AB、CD
的同一方(上方)。
2、在截线EF的
同旁(右侧)。
1
5
问题一:观察∠1和∠5,它们的位置有什么共同特点?
同位角
没有公共顶点的角的位置关系
A
B
C
D
E
F
图四
2
7
6
4
没有公共顶点的角的位置关系
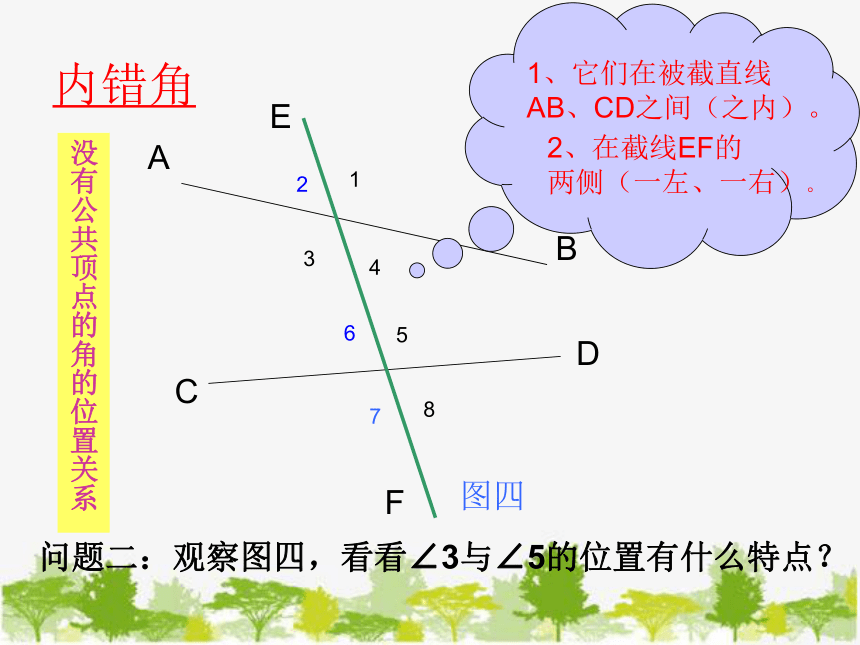
内错角
1、它们在被截直线
AB、CD之间(之内)。
2、在截线EF的
两侧(一左、一右)。
问题二:观察图四,看看∠3与∠5的位置有什么特点?
1
8
3
5
A
B
C
D
E
F
图四
2
7
6
没有公共顶点的角的位置关系
同旁内角
1、它们在两条被截直线
AB、CD之间(之内)。
2、在截线EF的
同一旁(同侧)。
问题三:看图四,观察∠3与∠6这对角的位置,
看看它们又有什么特点?
1
8
4
5
3
6
例1.如图,直线EF与AB,CD相交,构成8个角,指出图中所有的对顶角,同位角,内错角和同旁内角。
A
B
E
D
C
F
对顶角:∠1与∠3, ∠2与∠4, ∠5与∠7, ∠6与∠8
同位角:∠2与∠5, ∠1与∠8, ∠3与∠6, ∠4与∠7
内错角:∠1与∠6, ∠4与∠5
同旁内角:∠1与∠5, ∠4与∠6
随堂演练
2.指出下列各图中所有的同位角,内错角,
同旁内角.
1
2
3
4
5
6
7
8
a
b
c
同位角:∠2与∠5, ∠1与∠6, ∠3与∠8, ∠4与∠7
内错角:∠1与∠8, ∠4与∠5
同旁内角:∠1与∠5, ∠4与∠8
2、两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
1.对顶角相等。
课堂小结
3、如果两条直线被第三条直线所截有一组同位角相等,那么其它的同位角也相等,内错角也相等,同旁内角互补。
4、如果两条直线被第三条直线所截有一组内错角相等,那么另外一组内错角也相等,同位角相等,同旁内角互补。
5、如果两条直线被第三条直线所截有一组同旁内角互补,那么另外一组同旁内角也互补,同位角相等,内错角相等。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
湘教版 七年级下册
4.1.2 相交直线所成的角
D
C
B
A
O
1
2
有公共顶点,两边互为反向延长线,这样的两个角 叫做对顶角.
对顶角相等.
对 顶 角
推进新课
2、判断下列图形中哪对 1, 2是对顶角?
1
2
1
2
1
2
1、你能举出生活中包含对顶角的例子吗?
A
B
C
D
E
F
图四
2
3
6
7
8
4
1、都在被截直线AB、CD
的同一方(上方)。
2、在截线EF的
同旁(右侧)。
1
5
问题一:观察∠1和∠5,它们的位置有什么共同特点?
同位角
没有公共顶点的角的位置关系
A
B
C
D
E
F
图四
2
7
6
4
没有公共顶点的角的位置关系
内错角
1、它们在被截直线
AB、CD之间(之内)。
2、在截线EF的
两侧(一左、一右)。
问题二:观察图四,看看∠3与∠5的位置有什么特点?
1
8
3
5
A
B
C
D
E
F
图四
2
7
6
没有公共顶点的角的位置关系
同旁内角
1、它们在两条被截直线
AB、CD之间(之内)。
2、在截线EF的
同一旁(同侧)。
问题三:看图四,观察∠3与∠6这对角的位置,
看看它们又有什么特点?
1
8
4
5
3
6
例1.如图,直线EF与AB,CD相交,构成8个角,指出图中所有的对顶角,同位角,内错角和同旁内角。
A
B
E
D
C
F
对顶角:∠1与∠3, ∠2与∠4, ∠5与∠7, ∠6与∠8
同位角:∠2与∠5, ∠1与∠8, ∠3与∠6, ∠4与∠7
内错角:∠1与∠6, ∠4与∠5
同旁内角:∠1与∠5, ∠4与∠6
随堂演练
2.指出下列各图中所有的同位角,内错角,
同旁内角.
1
2
3
4
5
6
7
8
a
b
c
同位角:∠2与∠5, ∠1与∠6, ∠3与∠8, ∠4与∠7
内错角:∠1与∠8, ∠4与∠5
同旁内角:∠1与∠5, ∠4与∠8
2、两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
1.对顶角相等。
课堂小结
3、如果两条直线被第三条直线所截有一组同位角相等,那么其它的同位角也相等,内错角也相等,同旁内角互补。
4、如果两条直线被第三条直线所截有一组内错角相等,那么另外一组内错角也相等,同位角相等,同旁内角互补。
5、如果两条直线被第三条直线所截有一组同旁内角互补,那么另外一组同旁内角也互补,同位角相等,内错角相等。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
