19.2.3正方形课件
图片预览



文档简介
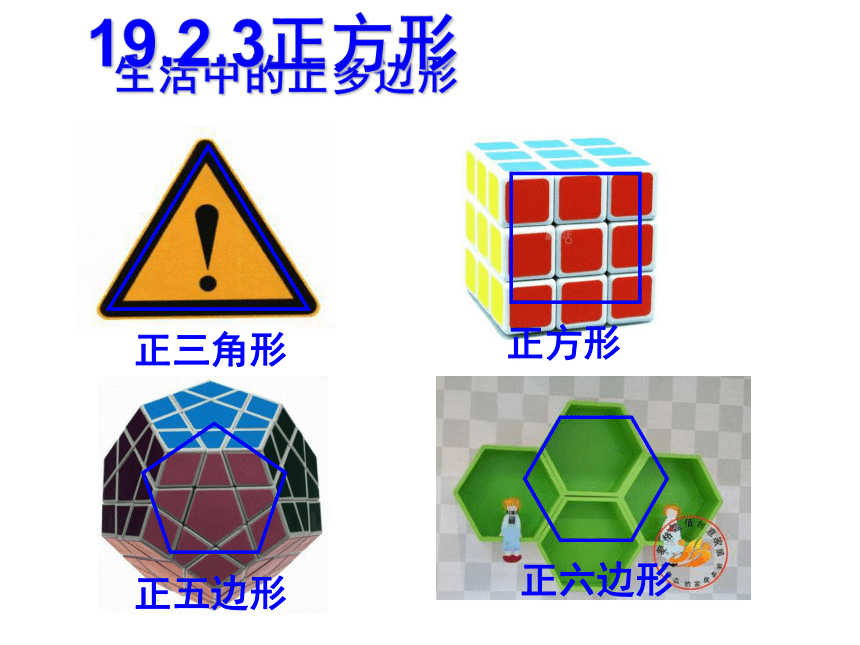
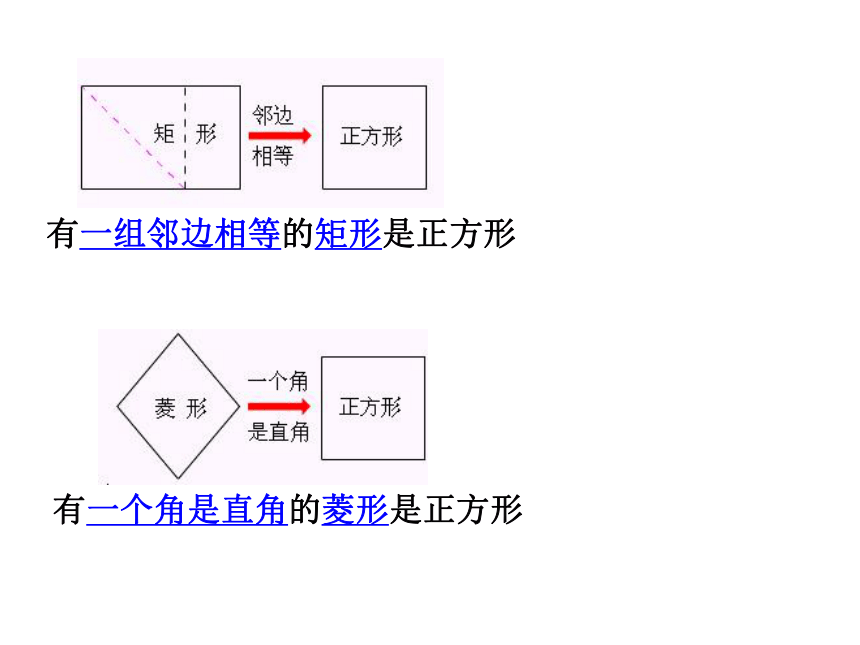
课件22张PPT。生活中的正多边形正三角形正方形正五边形正六边形19.2.3正方形有一组邻边相等的矩形是正方形有一个角是直角的菱形是正方形议一议 正方形是特殊的矩形,也是特殊的菱形。正方形的性质正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.BD√√√×(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )√3.下列说法对吗?辩一辩
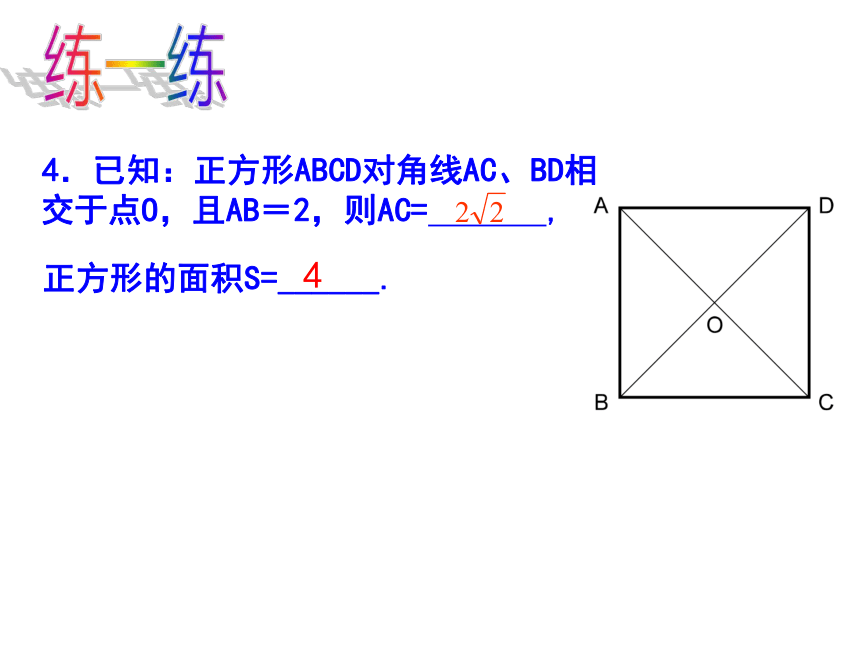
4.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2,则AC= ,
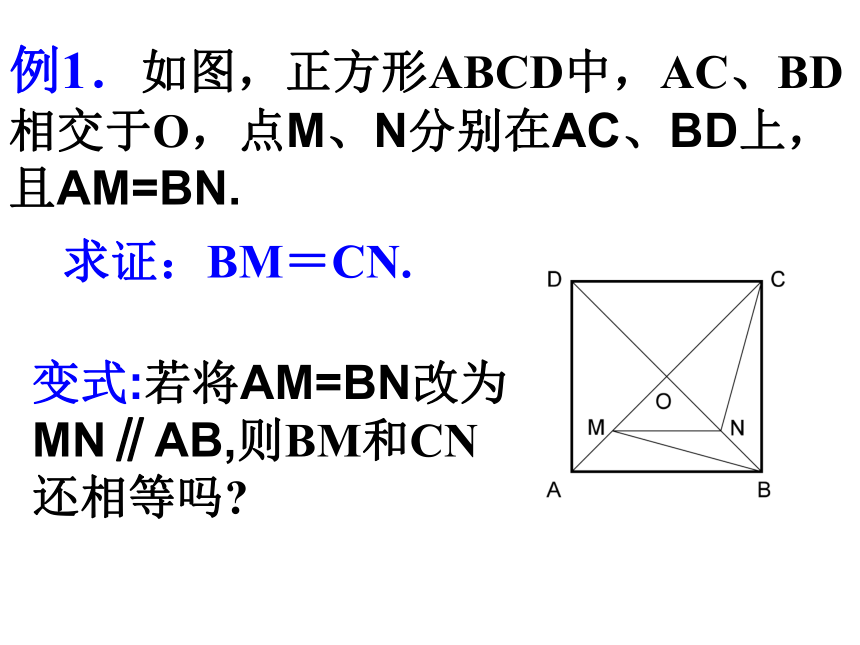
正方形的面积S=______. 练一练4 例1.如图,正方形ABCD中,AC、BD相交于O,点M、N分别在AC、BD上,且AM=BN.求证:BM=CN.变式:若将AM=BN改为
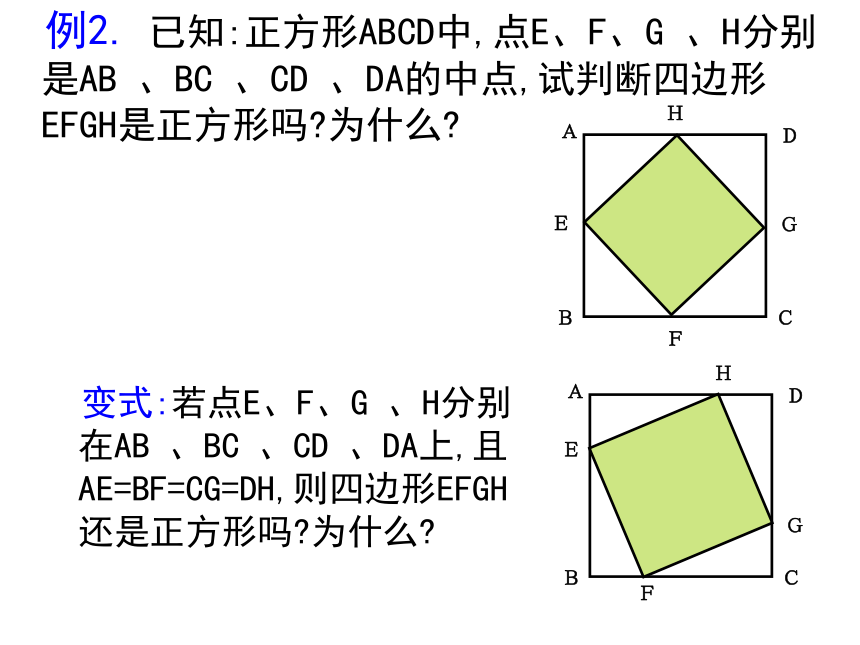
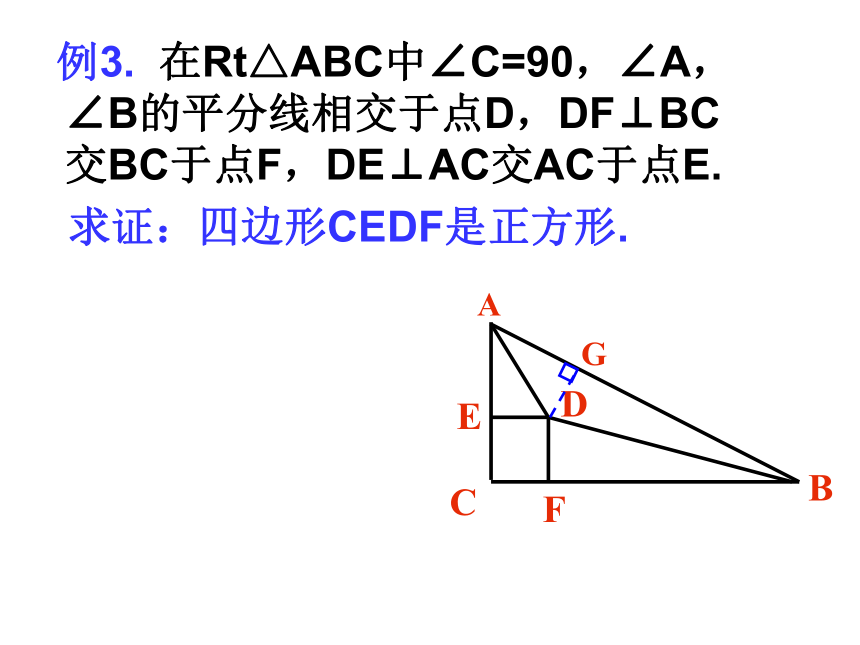
MN∥AB,则BM和CN还相等吗?例题解析 例2. 已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗?为什么? 变式:若点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,则四边形EFGH还是正方形吗?为什么? 例3. 在Rt△ABC中∠C=90,∠A,∠B的平分线相交于点D,DF⊥BC交BC于点F,DE⊥AC交AC于点E.
求证:四边形CEDF是正方形.FDCBEA练习1.在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F。
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)小结数学知识:1、正方形定义:有四个角相等,且四条边相等的四边形叫做正方形。2、正方形性质:
边: 对边平行,四边相等;
角: 四个角都是直角;
对角线: 相等,互相垂直平分,每条对角线平分一组对角;
对称性: 既是中心对称图形,又是轴对称图形。3、正方形判定:数学方法:转化为三角形的问题数学思想:转化思想,类比思想,一般到特殊的思想…… 平行四边形、矩形、菱形、正方形的关系。填一填平行四边形矩形菱形正方形1、ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?综合运用:2、设计花坛
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
综合运用:3、正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:(1)OE = OF EABCDOGF(2)若E是OB的延长线上的一点,OE = OF还成立吗? EABCDOGF 1、 已知:如图(4)在正方形ABCD中,F为CD 延长线 上一点,CE⊥AF于E,交AD于M.
求证:∠MFD=45° 课后思考2、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 (1)求证: △ACF≌△DCB(2) 猜想 BD与AF有何关系? 2、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 (3)当正方形AEDC绕点C旋转时,
BD与AF的关系还成立吗? 3、如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 (1)求证:CE=BG(2)当点A在平面移动时,结论是否还成立?(3)除此外,你还能得出哪些结论? 4、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF,探索图中AE与BF的关系。如图,在正方形ABCD中
如图(1)AE⊥BF ,AE与BF相等吗?FABCDEGGABCDEFHABCDEFGHM变式探究B.A.C.(1)(2)(3)如图(2)AE⊥HF ,AE与HF相等吗?如图(3)ME⊥HF , ME与HF相等吗?
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.BD√√√×(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )√3.下列说法对吗?辩一辩
4.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2,则AC= ,
正方形的面积S=______. 练一练4 例1.如图,正方形ABCD中,AC、BD相交于O,点M、N分别在AC、BD上,且AM=BN.求证:BM=CN.变式:若将AM=BN改为
MN∥AB,则BM和CN还相等吗?例题解析 例2. 已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗?为什么? 变式:若点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,则四边形EFGH还是正方形吗?为什么? 例3. 在Rt△ABC中∠C=90,∠A,∠B的平分线相交于点D,DF⊥BC交BC于点F,DE⊥AC交AC于点E.
求证:四边形CEDF是正方形.FDCBEA练习1.在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F。
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)小结数学知识:1、正方形定义:有四个角相等,且四条边相等的四边形叫做正方形。2、正方形性质:
边: 对边平行,四边相等;
角: 四个角都是直角;
对角线: 相等,互相垂直平分,每条对角线平分一组对角;
对称性: 既是中心对称图形,又是轴对称图形。3、正方形判定:数学方法:转化为三角形的问题数学思想:转化思想,类比思想,一般到特殊的思想…… 平行四边形、矩形、菱形、正方形的关系。填一填平行四边形矩形菱形正方形1、ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?综合运用:2、设计花坛
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
综合运用:3、正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:(1)OE = OF EABCDOGF(2)若E是OB的延长线上的一点,OE = OF还成立吗? EABCDOGF 1、 已知:如图(4)在正方形ABCD中,F为CD 延长线 上一点,CE⊥AF于E,交AD于M.
求证:∠MFD=45° 课后思考2、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 (1)求证: △ACF≌△DCB(2) 猜想 BD与AF有何关系? 2、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 (3)当正方形AEDC绕点C旋转时,
BD与AF的关系还成立吗? 3、如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 (1)求证:CE=BG(2)当点A在平面移动时,结论是否还成立?(3)除此外,你还能得出哪些结论? 4、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF,探索图中AE与BF的关系。如图,在正方形ABCD中
如图(1)AE⊥BF ,AE与BF相等吗?FABCDEGGABCDEFHABCDEFGHM变式探究B.A.C.(1)(2)(3)如图(2)AE⊥HF ,AE与HF相等吗?如图(3)ME⊥HF , ME与HF相等吗?
