20.3.3正方形 课件
图片预览


文档简介
课件36张PPT。标题/完美的正方形
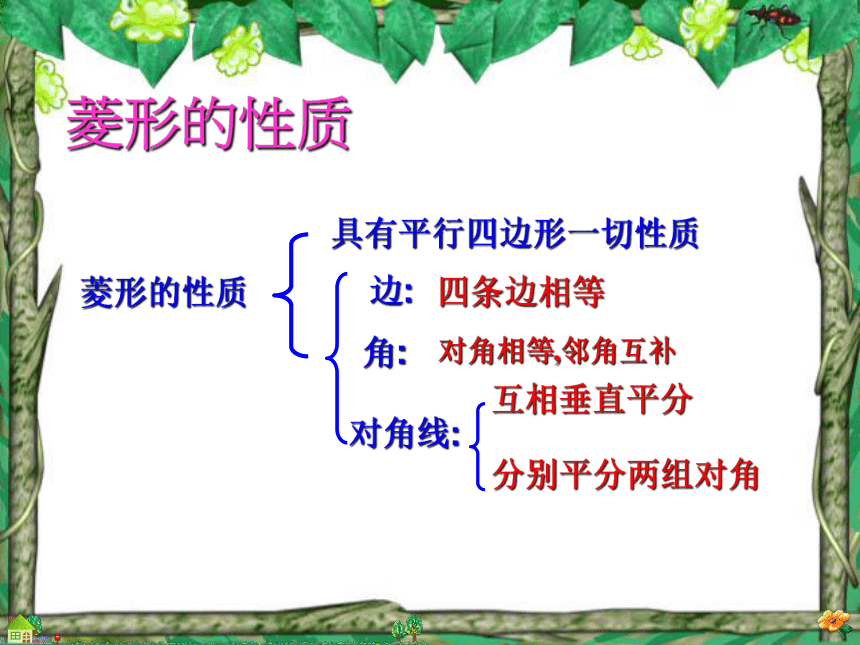
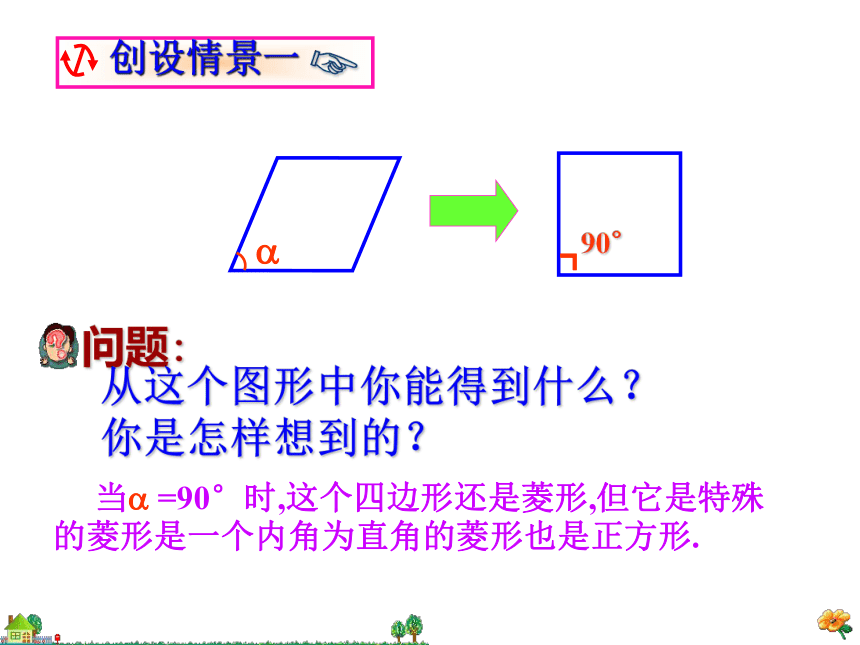
标题20.3.3 正方形复习回顾(1)平行四边形有哪些性质?矩形与平行四边形比较有哪些特殊的性质?平行四边形边:角:对角线:对边平行且相等对角相等,邻角互补对角线互相平分矩形角:四个角是直角对角线:对角线相等且互相平分边对边平行且相等菱形的性质菱形的性质边:四条边相等对角线:互相垂直平分分别平分两组对角角:具有平行四边形一切性质对角相等,邻角互补 创设情景一?问题: 从这个图形中你能得到什么?
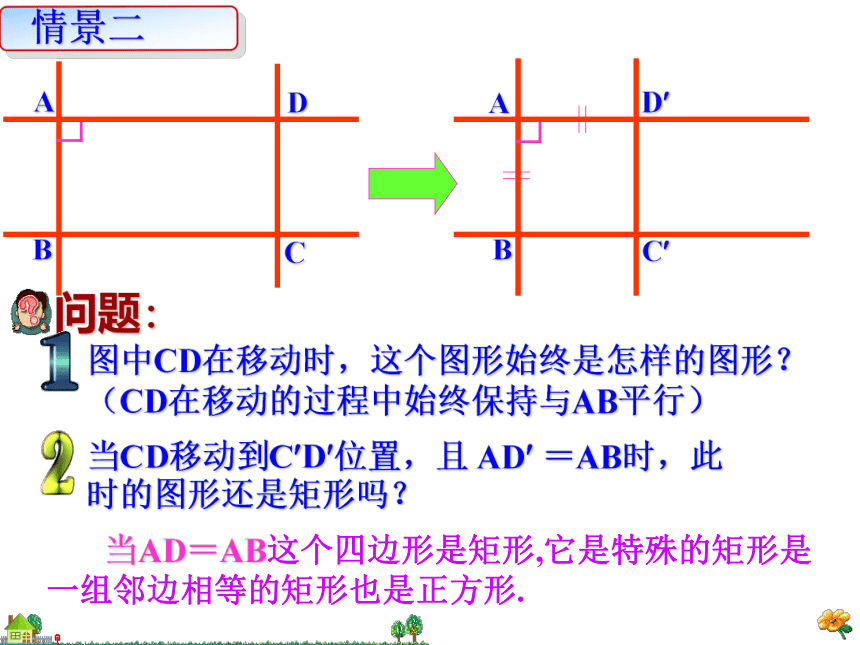
你是怎样想到的??┓90° 当? =90°时,这个四边形还是菱形,但它是特殊的菱形是一个内角为直角的菱形也是正方形.问题: 图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)当CD移动到C?D?位置,且 AD? =AB时,此
时的图形还是矩形吗?AB 当AD=AB这个四边形是矩形,它是特殊的矩形是一组邻边相等的矩形也是正方形.正方形的概念:
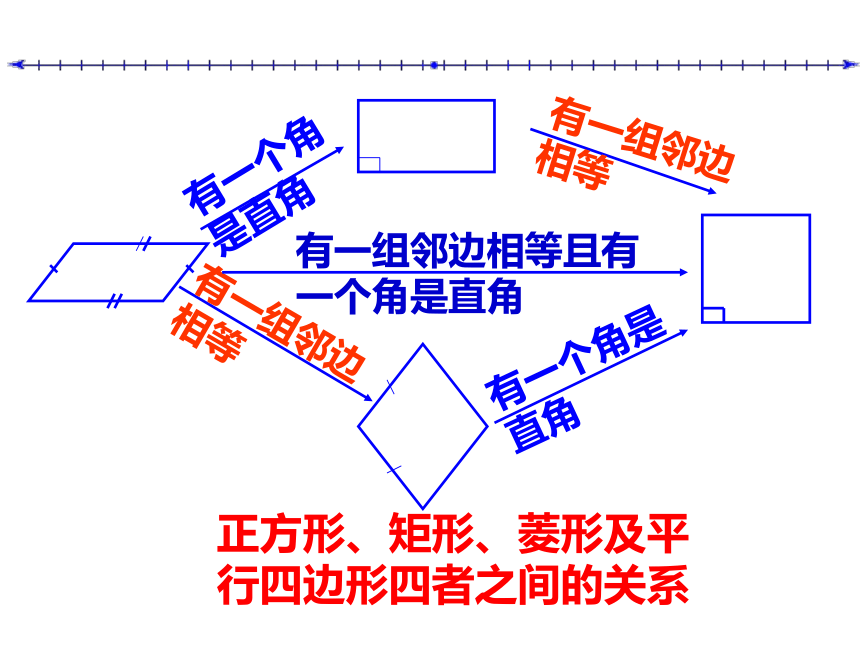
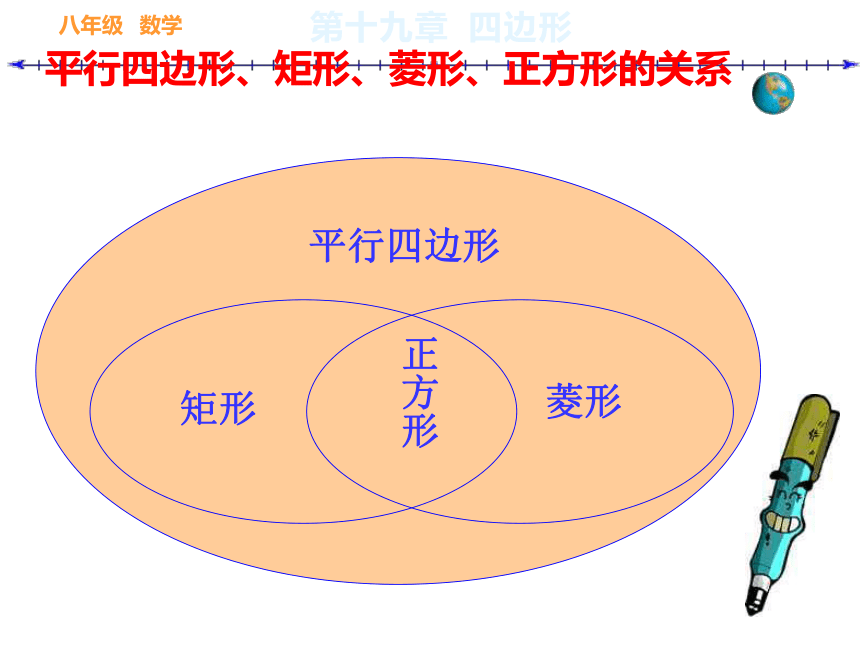
_______________________________ 的平行四边形是正方形。_______________的菱形是正方形_________________的矩形是正方形 定义法菱形法矩形法有一组邻边相等且有一个角是直角的有一个角是直角有一组邻边相等正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
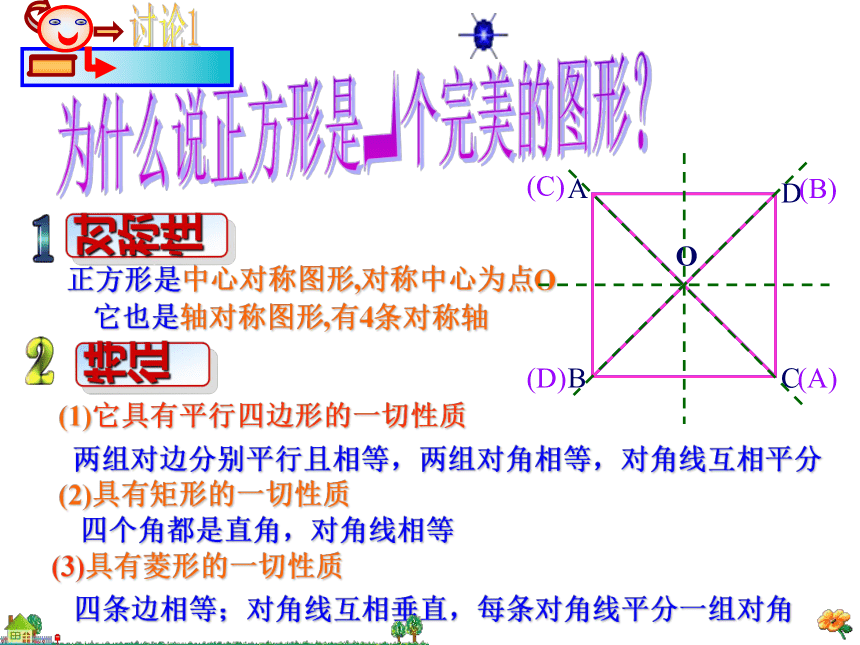
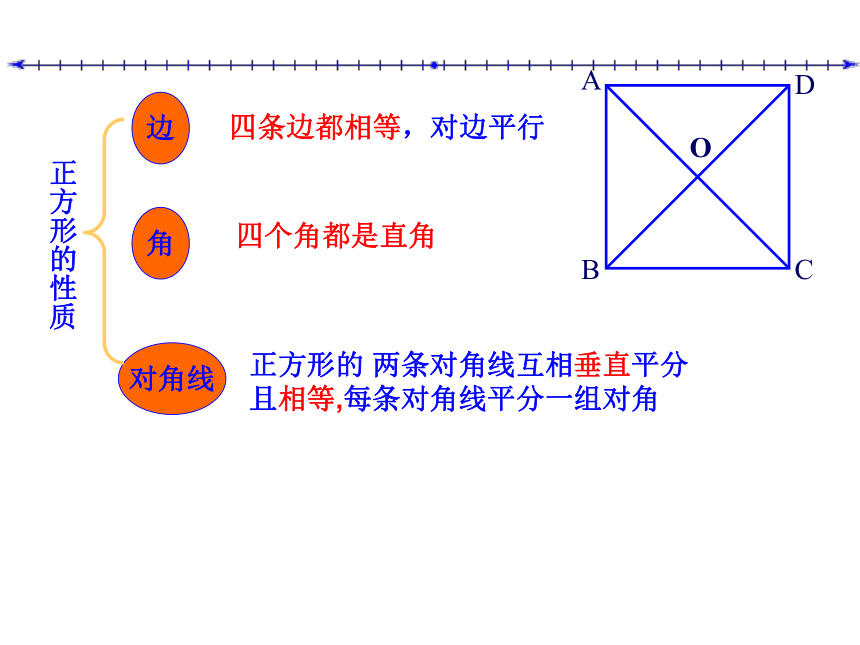
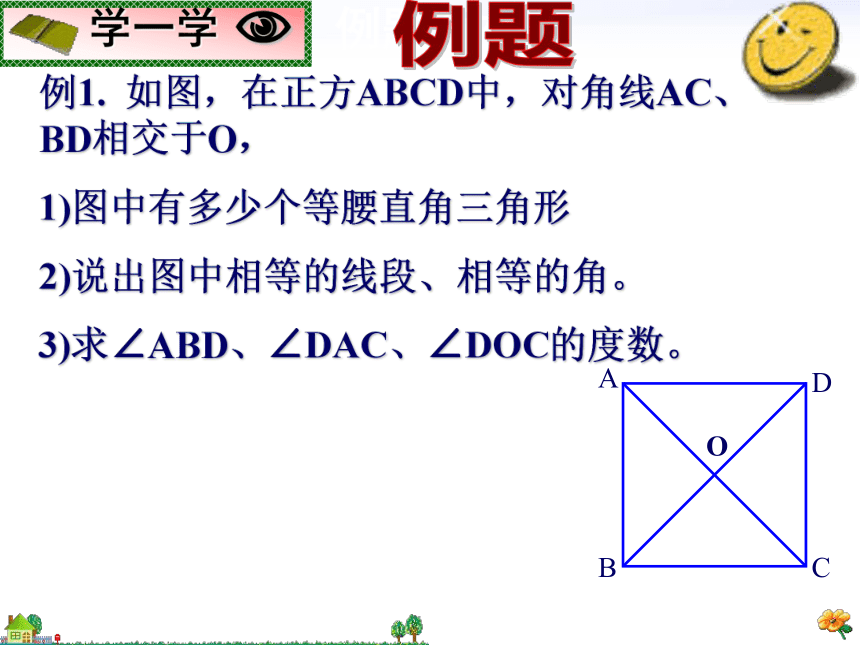
有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角正方形、矩形、菱形及平行四边形四者之间的关系平行四边形、矩形、菱形、正方形的关系正方形八年级 数学第十九章 四边形为什么说正方形是一个完美的图形?对称性特征正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角四条边都相等,对边平行四个角都是直角边对角线角正方形的性质例题解析例题例1. 如图,在正方ABCD中,对角线AC、BD相交于O,
1)图中有多少个等腰直角三角形
2)说出图中相等的线段、相等的角。
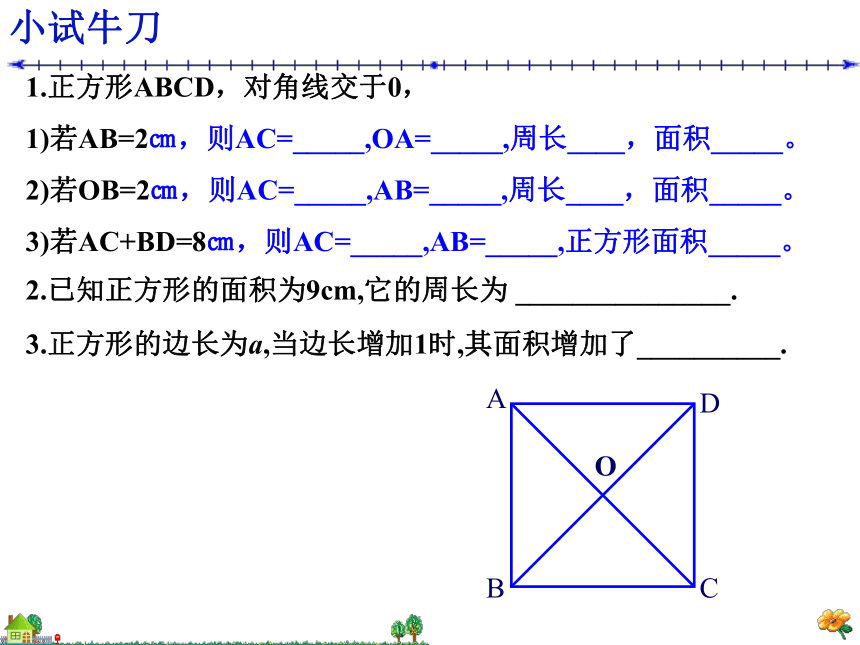
3)求∠ABD、∠DAC、∠DOC的度数。小试牛刀1.正方形ABCD,对角线交于0,
1)若AB=2㎝,则AC=_____,OA=_____,周长____,面积_____。
2)若OB=2㎝,则AC=_____,AB=_____,周长____,面积_____。
3)若AC+BD=8㎝,则AC=_____,AB=_____,正方形面积_____。
2.已知正方形的面积为9cm,它的周长为 _______________.3.正方形的边长为a,当边长增加1时,其面积增加了__________.正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD随堂练习 用10米长的篱笆围成一个四边形菜地,如何确定面积最大的四边形的形状,面积为多少?在长度给定的情况下,围成的四边形中,
正方形的面积最大。问题: 例2、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠E, ∠AFC的度数.F练习:1、如图,正方形ABCD中,BE=BD,求∠E练:正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.课堂练习例3.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.530°16cm2.以正方形ABCD的一边DC向外作等边△DCE,则∠AEB=_____.分析:PE=AE,PF=OE
PE+PF=OA正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.ABCDEF思考小结 1 .正方形是中心对称图形,轴对称图形。
2.正方形的四条边都相等。
3.正方形的四个角都相等。
4.正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。平行四边形正方形有一个角是直角一组邻边相等正方形既是菱形,又是矩形,因此正方形有下列性质: 正方形是轴对称图形,两条对角线所在直线,以及过每一组中点的直线都是它的对称轴.正方形的四条边都相等,四个角都是直角正方形的对角线相等,且互相垂直平分;每条对角线平分一组对角.正方形是中心对称图形,对角线的交点是它的对称中心. 学以致用小红在店里看到一块漂亮的方纱巾,
非常想买。但她拿起来看时感觉不太方。
商店老板看她犹豫的样子,马上过来
拉起一组对角,让小红看这组对角是
否对齐,小红还有些犹豫,老板又拉
起另一组对角,让小红检验。小红终
于买了这块纱巾。你认为小红买的这
块纱巾真是正方形吗?你能帮她检验吗? 学以致用分析:要判断是否是正方形,关键对折后
会得到什么条件。解:根据老板的方法,只能反映纱巾的两
组对角分别相等,四条边都相等,所以该
纱巾是菱形,但不一定是正方形。 由三条公路围成的一个区域为直角三角形形状.工程队要想在区域内划一块正方形的地块作为新小区,且让小区足够大,请你来帮工程队设计一下 .学以致用ABCDEF┓┓┓如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。 自主学习 例2.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG解:因为四边形ABCD是正方形根据正方形的四边相等,得AD=CD又知四边形DEFG也是正方形所以 DE=DG又因为正方形的每个内角为90°所以∠ADE+∠EDC=∠CDG+∠EDC所以∠ADE=∠CDG所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD所以AE=CG巩固练习:如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG
例3如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF例4.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF例4.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
例5.如图(3),正方形ABCD中,AC、BD相交于O, 分析:要证明BM=CN,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
AB=BC,∠1=∠2=45 ° AM=BN△ABM≌△BCN正方形ABCDOM=ON∠OMN=∠ONM=45°活动与探索如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450G变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展如何设计花坛?八年级 数学第十九章 四边形数一数图中正方形的个数,你发现了什么?多多多 ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识八年级 数学第十九章 四边形练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)小结√√√√√√√√√√√√√√√√√√√√√√谢谢大家!再见
标题20.3.3 正方形复习回顾(1)平行四边形有哪些性质?矩形与平行四边形比较有哪些特殊的性质?平行四边形边:角:对角线:对边平行且相等对角相等,邻角互补对角线互相平分矩形角:四个角是直角对角线:对角线相等且互相平分边对边平行且相等菱形的性质菱形的性质边:四条边相等对角线:互相垂直平分分别平分两组对角角:具有平行四边形一切性质对角相等,邻角互补 创设情景一?问题: 从这个图形中你能得到什么?
你是怎样想到的??┓90° 当? =90°时,这个四边形还是菱形,但它是特殊的菱形是一个内角为直角的菱形也是正方形.问题: 图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)当CD移动到C?D?位置,且 AD? =AB时,此
时的图形还是矩形吗?AB 当AD=AB这个四边形是矩形,它是特殊的矩形是一组邻边相等的矩形也是正方形.正方形的概念:
_______________________________ 的平行四边形是正方形。_______________的菱形是正方形_________________的矩形是正方形 定义法菱形法矩形法有一组邻边相等且有一个角是直角的有一个角是直角有一组邻边相等正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角正方形、矩形、菱形及平行四边形四者之间的关系平行四边形、矩形、菱形、正方形的关系正方形八年级 数学第十九章 四边形为什么说正方形是一个完美的图形?对称性特征正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角四条边都相等,对边平行四个角都是直角边对角线角正方形的性质例题解析例题例1. 如图,在正方ABCD中,对角线AC、BD相交于O,
1)图中有多少个等腰直角三角形
2)说出图中相等的线段、相等的角。
3)求∠ABD、∠DAC、∠DOC的度数。小试牛刀1.正方形ABCD,对角线交于0,
1)若AB=2㎝,则AC=_____,OA=_____,周长____,面积_____。
2)若OB=2㎝,则AC=_____,AB=_____,周长____,面积_____。
3)若AC+BD=8㎝,则AC=_____,AB=_____,正方形面积_____。
2.已知正方形的面积为9cm,它的周长为 _______________.3.正方形的边长为a,当边长增加1时,其面积增加了__________.正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD随堂练习 用10米长的篱笆围成一个四边形菜地,如何确定面积最大的四边形的形状,面积为多少?在长度给定的情况下,围成的四边形中,
正方形的面积最大。问题: 例2、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠E, ∠AFC的度数.F练习:1、如图,正方形ABCD中,BE=BD,求∠E练:正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.课堂练习例3.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.530°16cm2.以正方形ABCD的一边DC向外作等边△DCE,则∠AEB=_____.分析:PE=AE,PF=OE
PE+PF=OA正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.ABCDEF思考小结 1 .正方形是中心对称图形,轴对称图形。
2.正方形的四条边都相等。
3.正方形的四个角都相等。
4.正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。平行四边形正方形有一个角是直角一组邻边相等正方形既是菱形,又是矩形,因此正方形有下列性质: 正方形是轴对称图形,两条对角线所在直线,以及过每一组中点的直线都是它的对称轴.正方形的四条边都相等,四个角都是直角正方形的对角线相等,且互相垂直平分;每条对角线平分一组对角.正方形是中心对称图形,对角线的交点是它的对称中心. 学以致用小红在店里看到一块漂亮的方纱巾,
非常想买。但她拿起来看时感觉不太方。
商店老板看她犹豫的样子,马上过来
拉起一组对角,让小红看这组对角是
否对齐,小红还有些犹豫,老板又拉
起另一组对角,让小红检验。小红终
于买了这块纱巾。你认为小红买的这
块纱巾真是正方形吗?你能帮她检验吗? 学以致用分析:要判断是否是正方形,关键对折后
会得到什么条件。解:根据老板的方法,只能反映纱巾的两
组对角分别相等,四条边都相等,所以该
纱巾是菱形,但不一定是正方形。 由三条公路围成的一个区域为直角三角形形状.工程队要想在区域内划一块正方形的地块作为新小区,且让小区足够大,请你来帮工程队设计一下 .学以致用ABCDEF┓┓┓如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。 自主学习 例2.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG解:因为四边形ABCD是正方形根据正方形的四边相等,得AD=CD又知四边形DEFG也是正方形所以 DE=DG又因为正方形的每个内角为90°所以∠ADE+∠EDC=∠CDG+∠EDC所以∠ADE=∠CDG所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD所以AE=CG巩固练习:如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG
例3如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF例4.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF例4.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
例5.如图(3),正方形ABCD中,AC、BD相交于O, 分析:要证明BM=CN,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
AB=BC,∠1=∠2=45 ° AM=BN△ABM≌△BCN正方形ABCDOM=ON∠OMN=∠ONM=45°活动与探索如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450G变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展如何设计花坛?八年级 数学第十九章 四边形数一数图中正方形的个数,你发现了什么?多多多 ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识八年级 数学第十九章 四边形练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)小结√√√√√√√√√√√√√√√√√√√√√√谢谢大家!再见
