苏教版六年数学下册图形与几何综合质量监测题(含答案)
文档属性
| 名称 | 苏教版六年数学下册图形与几何综合质量监测题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 243.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览



文档简介
苏教版六年数学下册图形与几何综合质量监测题班级:_____姓名:_______座号:______评价:
一、选择题(18%)
1.将一根长厘米的铁丝截成三段围成三角形,最长的一段最长是()厘米。(取整厘米数)
A. B. C. D.
2.芳芳家在红红家北偏西的方向上,那么红红家在芳芳家()的方向上。
A.北偏西 B.南偏北 C.南偏东 D.北偏东
3.用数对表示丽丽的座位是,与她相邻的前面一个同学的座位用数对表示是()。
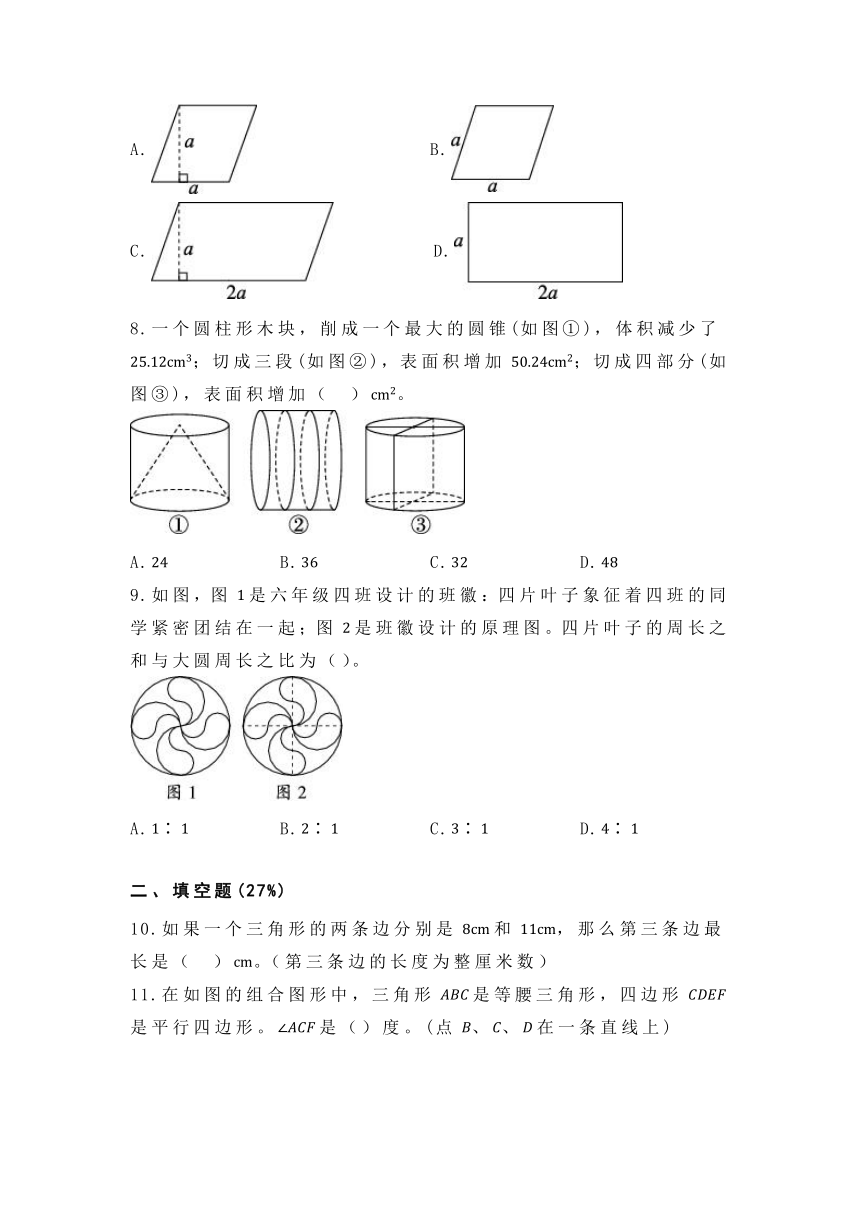
A. B. C. D.
4.在下列问题中,问题()需要计算物体的体积。
A.包装一份生日礼物需要多少彩纸
B.给大厅里的柱子刷油漆,需要多少油漆
C.装饰黑板的四周,需要多少彩带
D.一个铁球沉入装满水的容器中,溢出多少水
5.一个长方体盒子,从里面量,长、宽、高。如果把棱长的正方体积木装进盒子,并使积木不外露,最多可以装()块。
A. B. C. D.
6.用个同样大小的正方体拼成一个立体图形,从上面、正面和左面看到的形状完全一样,这个立体图形是()。
A. B. C. D.
7.一个圆柱的底面半径和高的比是∶,下面()图形是这个圆柱侧面的展开图。
A. B.
C. D.
8.一个圆柱形木块,削成一个最大的圆锥(如图①),体积减少了;切成三段(如图②),表面积增加;切成四部分(如图③),表面积增加( )。
A. B. C. D.
9.如图,图是六年级四班设计的班徽:四片叶子象征着四班的同学紧密团结在一起;图是班徽设计的原理图。四片叶子的周长之和与大圆周长之比为()。
A.∶ B.∶ C.∶ D.∶
二、填空题(27%)
10.如果一个三角形的两条边分别是和,那么第三条边最长是( )。(第三条边的长度为整厘米数)
11.在如图的组合图形中,三角形是等腰三角形,四边形是平行四边形。是()度。(点、、在一条直线上)
12.下面是一个正方体的展开图,如果相对的两个面上的数字之和为,那么( )。
13.如图,正方形的周长是,则平行四边形的面积是( ),三角形的面积是( )。
14.如图,酒瓶中的圆柱部分装满酒,倒进右侧的酒杯中,酒杯的直径是酒瓶直径的一半,共能倒满 ( )杯。(单位:厘米)
15.图中一个小球的体积是()立方厘米,一个大球的体积是()立方厘米。(单位:厘米)
16.三个长方体鱼缸,每个鱼缸相交于一个顶点的三条棱的长度都是,,但底面各不相同。现在往每个鱼缸里都注入深的水,再把其中一个鱼缸的水倒入另一个鱼缸,则此时被倒入水的鱼缸中水的深度至少( )。
17.在圆的面积公式推导过程中,李明将自己做的圆转化成一个近似的长方形,这个长方形的周长比圆的周长多了。请你试画出这个圆,并计算出它的面积。
18.如下图,平行四边形的面积是平方厘米,圆的面积是( )平方厘米。
三、解答题(32%)
19.如图,梯形的面积是,求阴影部分的面积。
20.计算下面图形的体积。(单位:)
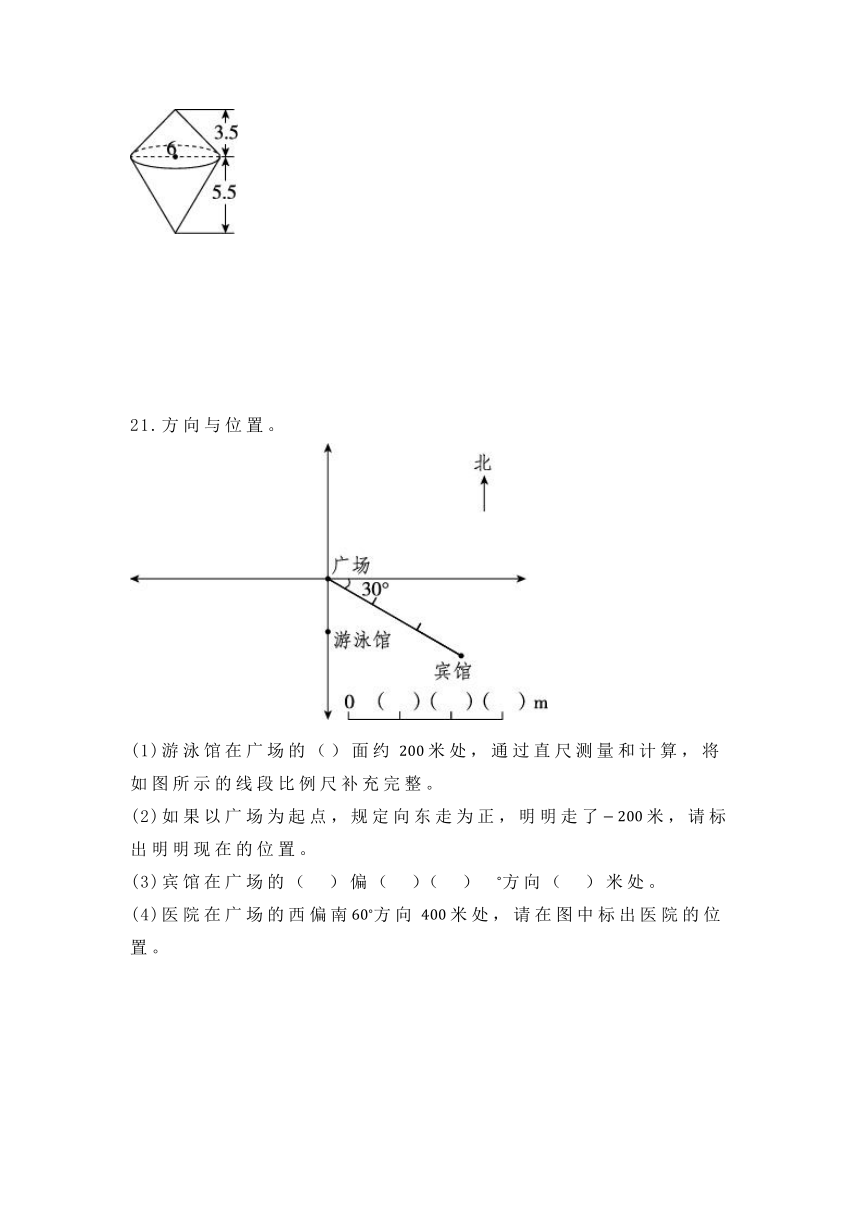
21.方向与位置。
(1)游泳馆在广场的()面约米处,通过直尺测量和计算,将如图所示的线段比例尺补充完整。
(2)如果以广场为起点,规定向东走为正,明明走了米,请标出明明现在的位置。
(3)宾馆在广场的( )偏( )( )方向( )米处。
(4)医院在广场的西偏南方向米处,请在图中标出医院的位置。
22.在下面的直角梯形中,三角形和三角形都是等腰直角三角形,且,那么直角梯形的面积是多少?
23.下面是一个直角三角形。边上的高是多少厘米?(先在图中画出高,再计算)以边为轴旋转一周形成的立体图形的体积是多少?
24.欣欣帽子厂设计的礼帽如图所示,帽顶部分是圆柱形,帽檐部分是一个圆环,其中帽顶的半径、高及帽檐的宽都是,做这样一顶帽子至少需要多少平方分米的布料?
25.乒乓球的直径是厘米个乒乓球正好能放在一个有盖的盒子里。请你先猜想一下,这是一个怎样的盒子,做这样一个盒子需要用多少平方厘米的纸板?(纸板厚度忽略不计)
要求:①先画出草图,再解决问题。②至少写出两种不同的方案。
26.探索与发现。
(1)图中每个小长方形的长都是,宽都是,个这样的小长方形按照如图所示摆放成一个大长方形。这个大长方形的周长是多少厘米?
(2)如果给你个长、宽的小长方形,你能把它们按照这种方式摆出一个大长方形吗?如果能,请你画出示意图;如果不能,请你说明理由。
(3)小宇用个小长方形按照第题中的方式摆出了一个大长方形。他所用的小长方形的长、宽可能是多少?请你写出种,填在下表中。
长
宽
根据上面的探索,你有什么发现?
四、操作题(10%)
27.按要求在下面的方格图中画图并完成填空。
(1)画出平行四边形向左平移格后的图形,平移后点的对应点的位置用数对表示是( )。
(2)画出平行四边形绕点顺时针旋转后的图形。
(3)已知一个轴对称图形的是图①,请在合适的位置把这个轴对称图形画出来。
(4)画出图②按∶的比放大后的图形。
五、解决问题(13%,其中28题6分,29题7分。)
28.某地下排水管道的横截面是正方形,边长为米,暴雨时经常排水不畅,导致地面积水。现在改为直径是米的圆柱形管道(如图)。假设暴雨时,管道中水流的速度均为米/秒。改造后,秒钟可以多排水多少立方米?(管道壁的厚度不计)
29.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示,瓶内药水的体积为。瓶子正放时,瓶内液面的高为瓶子倒放时,空余部分高。这个瓶子的容积是多少立方厘米?
参考答案
1.【答案】:B
2.【答案】:C
3.【答案】:A
4.【答案】:D
5.【答案】:C
6.【答案】:C
7.【答案】:A
8.【答案】:D
9.【答案】:B
【解析】:根据题意,设大圆的直径为厘米,则每片叶子中大半圆的直径为厘米,每片叶子中小半圆的直径为厘米,根据圆的周长公式:把数据代入公式分别求出四片叶子的周长之和与大圆周长,进而求出它们的周长之比。
10.【答案】:
11.【答案】:
12.【答案】:
13.【答案】:;
14.【答案】:
【解析】:设酒杯的半径是高是酒杯的容积,酒瓶中酒的体积,能倒的杯数就是(杯)。
15.【答案】:;
16.【答案】:
【解析】:已知三个长方体相交于一个顶点的三条棱的长度都是,,但底面各不相同。因此可知:这三个鱼缸的底面积分别是平方分米、平方分米、平方分米,将底面积最小的鱼缸中的水倒入底面积最大的鱼缸中,水的深度最小,根据长方体的体积公式:,那么,把数据代入公式解答。
17.【答案】:
18.【答案】:
19.【答案】:
20.【答案】:
21
(1)【答案】正南
(2)【答案】
(3)【答案】南;东;;
(4)【答案】
22.【答案】:
【解析】:根据题意可知,梯形的上底与下底的长度和正好是梯形的高的长度,然后带入梯形面积公式计算即可。
23.【答案】:
【解析】:根据三角形的面积公式:,那么,据此可以求出边上的高是多少厘米,以边为轴旋转一周形成的立体图形是两个同底的圆锥,两个圆锥高的和是厘米,根据圆锥的体积公式计算即可。
24.【答案】:帽顶的面积:
帽沿的面积:
答:做这样一顶帽子至少需要平方分米的布料。
25.【答案】:方案一:(厘米)
方案一:(厘米)
方案一 方案二
【解析】:根据题意,可以这样设计盒子,盒子长厘米、宽厘米、高厘米;也可以设计为:盒子长厘米、宽厘米、高厘米,根据长方体的表面积公式:,把数据代入公式即可求出需要纸板的面积。方案合理即可。
26(1)【答案】
(2)【答案】不能摆出一个大长方形,因为 ,所以不能。
(3)【答案】答案不唯一,如:
长
宽
我发现:所用的小长方形的长和宽之间有这样的规律:长∶宽∶。
27(1)【答案】
(2)【答案】
(3)【答案】(画法不唯一)
(4)【答案】
28.【答案】:
答:改造后,分钟可以多排水。
【解析】:改造前水在水管内的形状是长方体,可利用求出每秒流水的体积;改造后水在水管内的形状是圆柱体,可利用求出每秒流水的体积,据此相减即可。
29.【答案】:
答:这个瓶子的容积是。
一、选择题(18%)
1.将一根长厘米的铁丝截成三段围成三角形,最长的一段最长是()厘米。(取整厘米数)
A. B. C. D.
2.芳芳家在红红家北偏西的方向上,那么红红家在芳芳家()的方向上。
A.北偏西 B.南偏北 C.南偏东 D.北偏东
3.用数对表示丽丽的座位是,与她相邻的前面一个同学的座位用数对表示是()。
A. B. C. D.
4.在下列问题中,问题()需要计算物体的体积。
A.包装一份生日礼物需要多少彩纸
B.给大厅里的柱子刷油漆,需要多少油漆
C.装饰黑板的四周,需要多少彩带
D.一个铁球沉入装满水的容器中,溢出多少水
5.一个长方体盒子,从里面量,长、宽、高。如果把棱长的正方体积木装进盒子,并使积木不外露,最多可以装()块。
A. B. C. D.
6.用个同样大小的正方体拼成一个立体图形,从上面、正面和左面看到的形状完全一样,这个立体图形是()。
A. B. C. D.
7.一个圆柱的底面半径和高的比是∶,下面()图形是这个圆柱侧面的展开图。
A. B.
C. D.
8.一个圆柱形木块,削成一个最大的圆锥(如图①),体积减少了;切成三段(如图②),表面积增加;切成四部分(如图③),表面积增加( )。
A. B. C. D.
9.如图,图是六年级四班设计的班徽:四片叶子象征着四班的同学紧密团结在一起;图是班徽设计的原理图。四片叶子的周长之和与大圆周长之比为()。
A.∶ B.∶ C.∶ D.∶
二、填空题(27%)
10.如果一个三角形的两条边分别是和,那么第三条边最长是( )。(第三条边的长度为整厘米数)
11.在如图的组合图形中,三角形是等腰三角形,四边形是平行四边形。是()度。(点、、在一条直线上)
12.下面是一个正方体的展开图,如果相对的两个面上的数字之和为,那么( )。
13.如图,正方形的周长是,则平行四边形的面积是( ),三角形的面积是( )。
14.如图,酒瓶中的圆柱部分装满酒,倒进右侧的酒杯中,酒杯的直径是酒瓶直径的一半,共能倒满 ( )杯。(单位:厘米)
15.图中一个小球的体积是()立方厘米,一个大球的体积是()立方厘米。(单位:厘米)
16.三个长方体鱼缸,每个鱼缸相交于一个顶点的三条棱的长度都是,,但底面各不相同。现在往每个鱼缸里都注入深的水,再把其中一个鱼缸的水倒入另一个鱼缸,则此时被倒入水的鱼缸中水的深度至少( )。
17.在圆的面积公式推导过程中,李明将自己做的圆转化成一个近似的长方形,这个长方形的周长比圆的周长多了。请你试画出这个圆,并计算出它的面积。
18.如下图,平行四边形的面积是平方厘米,圆的面积是( )平方厘米。
三、解答题(32%)
19.如图,梯形的面积是,求阴影部分的面积。
20.计算下面图形的体积。(单位:)
21.方向与位置。
(1)游泳馆在广场的()面约米处,通过直尺测量和计算,将如图所示的线段比例尺补充完整。
(2)如果以广场为起点,规定向东走为正,明明走了米,请标出明明现在的位置。
(3)宾馆在广场的( )偏( )( )方向( )米处。
(4)医院在广场的西偏南方向米处,请在图中标出医院的位置。
22.在下面的直角梯形中,三角形和三角形都是等腰直角三角形,且,那么直角梯形的面积是多少?
23.下面是一个直角三角形。边上的高是多少厘米?(先在图中画出高,再计算)以边为轴旋转一周形成的立体图形的体积是多少?
24.欣欣帽子厂设计的礼帽如图所示,帽顶部分是圆柱形,帽檐部分是一个圆环,其中帽顶的半径、高及帽檐的宽都是,做这样一顶帽子至少需要多少平方分米的布料?
25.乒乓球的直径是厘米个乒乓球正好能放在一个有盖的盒子里。请你先猜想一下,这是一个怎样的盒子,做这样一个盒子需要用多少平方厘米的纸板?(纸板厚度忽略不计)
要求:①先画出草图,再解决问题。②至少写出两种不同的方案。
26.探索与发现。
(1)图中每个小长方形的长都是,宽都是,个这样的小长方形按照如图所示摆放成一个大长方形。这个大长方形的周长是多少厘米?
(2)如果给你个长、宽的小长方形,你能把它们按照这种方式摆出一个大长方形吗?如果能,请你画出示意图;如果不能,请你说明理由。
(3)小宇用个小长方形按照第题中的方式摆出了一个大长方形。他所用的小长方形的长、宽可能是多少?请你写出种,填在下表中。
长
宽
根据上面的探索,你有什么发现?
四、操作题(10%)
27.按要求在下面的方格图中画图并完成填空。
(1)画出平行四边形向左平移格后的图形,平移后点的对应点的位置用数对表示是( )。
(2)画出平行四边形绕点顺时针旋转后的图形。
(3)已知一个轴对称图形的是图①,请在合适的位置把这个轴对称图形画出来。
(4)画出图②按∶的比放大后的图形。
五、解决问题(13%,其中28题6分,29题7分。)
28.某地下排水管道的横截面是正方形,边长为米,暴雨时经常排水不畅,导致地面积水。现在改为直径是米的圆柱形管道(如图)。假设暴雨时,管道中水流的速度均为米/秒。改造后,秒钟可以多排水多少立方米?(管道壁的厚度不计)
29.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示,瓶内药水的体积为。瓶子正放时,瓶内液面的高为瓶子倒放时,空余部分高。这个瓶子的容积是多少立方厘米?
参考答案
1.【答案】:B
2.【答案】:C
3.【答案】:A
4.【答案】:D
5.【答案】:C
6.【答案】:C
7.【答案】:A
8.【答案】:D
9.【答案】:B
【解析】:根据题意,设大圆的直径为厘米,则每片叶子中大半圆的直径为厘米,每片叶子中小半圆的直径为厘米,根据圆的周长公式:把数据代入公式分别求出四片叶子的周长之和与大圆周长,进而求出它们的周长之比。
10.【答案】:
11.【答案】:
12.【答案】:
13.【答案】:;
14.【答案】:
【解析】:设酒杯的半径是高是酒杯的容积,酒瓶中酒的体积,能倒的杯数就是(杯)。
15.【答案】:;
16.【答案】:
【解析】:已知三个长方体相交于一个顶点的三条棱的长度都是,,但底面各不相同。因此可知:这三个鱼缸的底面积分别是平方分米、平方分米、平方分米,将底面积最小的鱼缸中的水倒入底面积最大的鱼缸中,水的深度最小,根据长方体的体积公式:,那么,把数据代入公式解答。
17.【答案】:
18.【答案】:
19.【答案】:
20.【答案】:
21
(1)【答案】正南
(2)【答案】
(3)【答案】南;东;;
(4)【答案】
22.【答案】:
【解析】:根据题意可知,梯形的上底与下底的长度和正好是梯形的高的长度,然后带入梯形面积公式计算即可。
23.【答案】:
【解析】:根据三角形的面积公式:,那么,据此可以求出边上的高是多少厘米,以边为轴旋转一周形成的立体图形是两个同底的圆锥,两个圆锥高的和是厘米,根据圆锥的体积公式计算即可。
24.【答案】:帽顶的面积:
帽沿的面积:
答:做这样一顶帽子至少需要平方分米的布料。
25.【答案】:方案一:(厘米)
方案一:(厘米)
方案一 方案二
【解析】:根据题意,可以这样设计盒子,盒子长厘米、宽厘米、高厘米;也可以设计为:盒子长厘米、宽厘米、高厘米,根据长方体的表面积公式:,把数据代入公式即可求出需要纸板的面积。方案合理即可。
26(1)【答案】
(2)【答案】不能摆出一个大长方形,因为 ,所以不能。
(3)【答案】答案不唯一,如:
长
宽
我发现:所用的小长方形的长和宽之间有这样的规律:长∶宽∶。
27(1)【答案】
(2)【答案】
(3)【答案】(画法不唯一)
(4)【答案】
28.【答案】:
答:改造后,分钟可以多排水。
【解析】:改造前水在水管内的形状是长方体,可利用求出每秒流水的体积;改造后水在水管内的形状是圆柱体,可利用求出每秒流水的体积,据此相减即可。
29.【答案】:
答:这个瓶子的容积是。
