3.1.2 椭圆的简单几何性质 课件(共24张PPT)
文档属性
| 名称 | 3.1.2 椭圆的简单几何性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 23:30:26 | ||
图片预览





文档简介
(共24张PPT)
3.1.2椭圆的简单几何性质
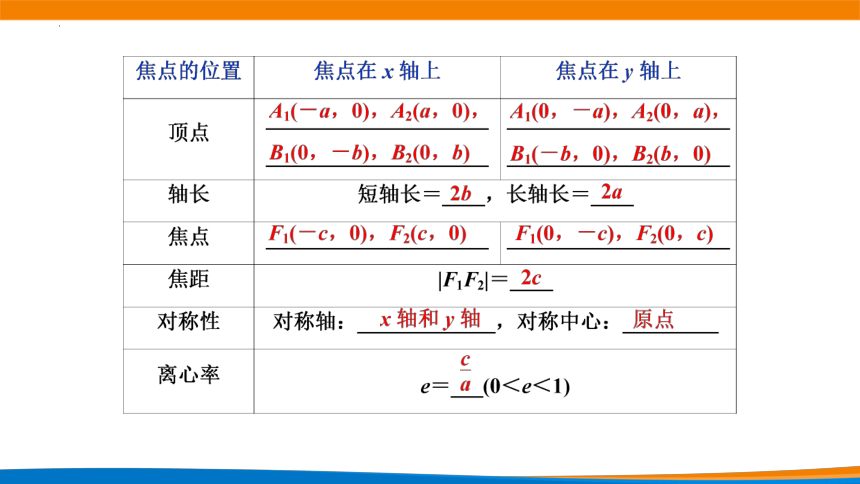
1、复习巩固
2、课堂探究
探究1:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点,为坐标原点. 探究:当在何位置时,最小?又在何位置时,最大?
设
则
因为
所以
所以
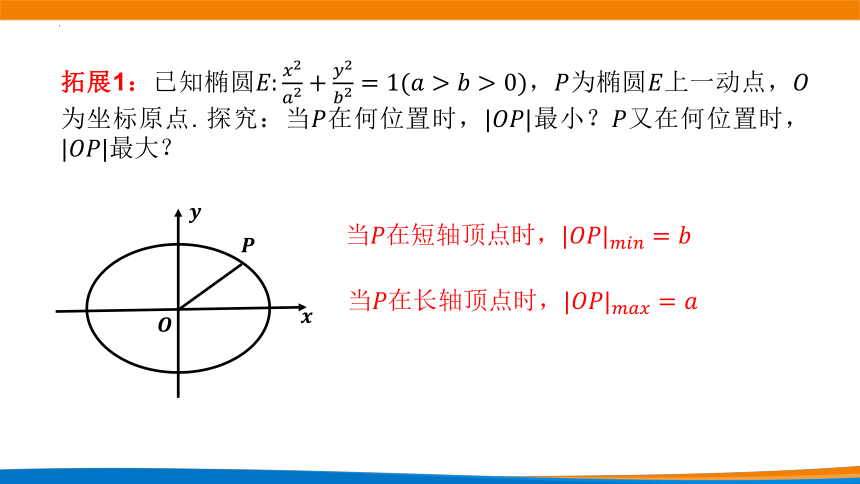
拓展1:已知椭圆,为椭圆上一动点,为坐标原点. 探究:当在何位置时,最小?又在何位置时,最大?
当在短轴顶点时,
当在长轴顶点时,
2、课堂探究
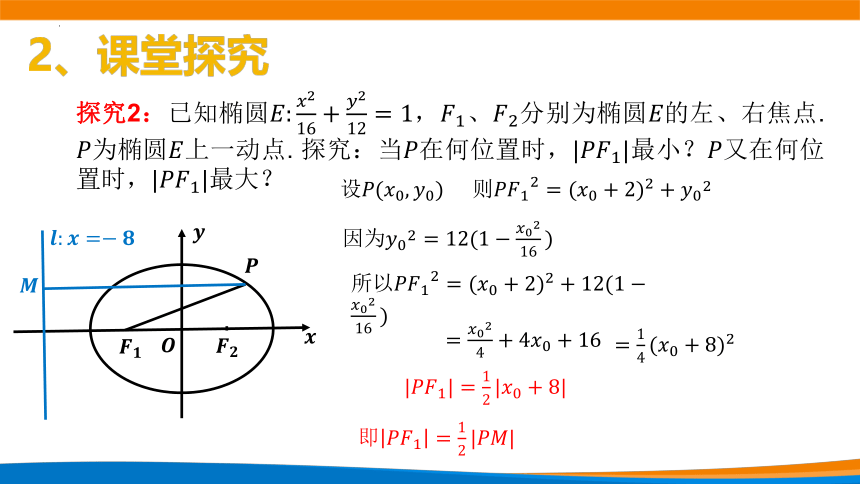
探究2:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点. 探究:当在何位置时,最小?又在何位置时,最大?
设
则
因为
所以
即
拓展2:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点. 探究:当在何位置时,最小?又在何位置时,最大?
设
则
因为
所以
即
椭圆,、分别为椭圆的左、右焦点,为椭圆上一动点.
, .
左准线
右准线
焦半径公式
3、课后巩固
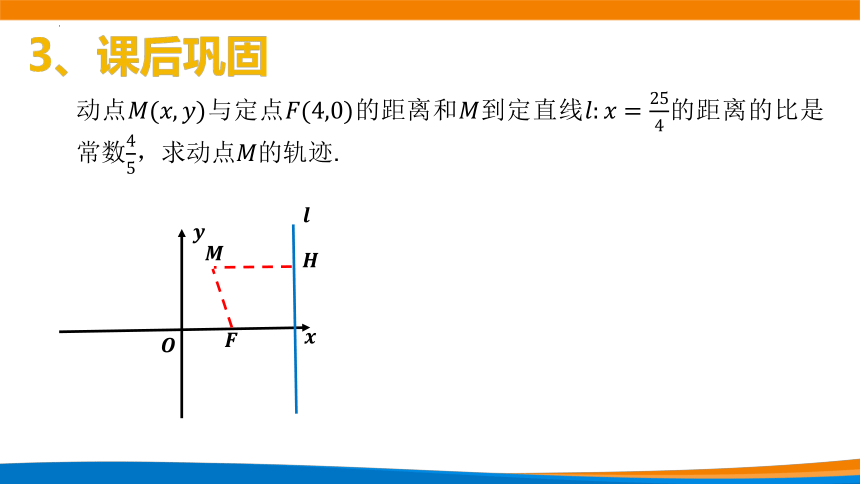
动点与定点的距离和到定直线的距离的比是常数,求动点的轨迹.
4、课后探究
探究1:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点. 探究:当在何位置时,最大?又在何位置时,最小?
4、课后探究
探究2:已知椭圆,、分别为椭圆的左、右顶点. 为椭圆上一动点. 探究:当在何位置时,最大?又在何位置时,最小?
5、课堂小结
椭圆,、分别为椭圆的左、右焦点,坐标原点,为椭圆上一动点.
(1)到左焦点的距离与它到左准线的距离的比为离心率,即 ,;
(2)到右焦点的距离与它到右准线的距离的比为离心率即,
(3), ;
(4), .
5、课堂小结
数学思想方法:
消元思想
从特殊到一般思想
数形结合思想
再会!
(第二课时)
3.1.2椭圆的简单几何性质
椭圆与直线的关系
直线和椭圆可以有哪些关系?
相交
相离
相切
给出解析式,如何判断是哪种情况?
相切、相交、相离的本质是什么?
交点个数:
1,2,0
问题化为求交点个数的问题
交点的本质是什么?
交点是同时满足两个曲线方程的点
交点个数=方程组解的个数
如何求方程组的解
代入!
①
②
①
②
怎么代入?
①化为
代入②
转变为:
关于的一元二次方程
一元二次方程的解有哪些情况?
无解
有两个相同的解
有两个不同的解
相离
相切
相离
来实战!
例题1:直线
和椭圆
解:
由方程组
①
②
代入②得
代入①,得到
的关系是?若有交点,求出交点坐标
化简得到
交点为
得到交点的纵坐标!
这就是交点的横坐标!
例题2已知直线
和椭圆
为何值时,直线
与椭圆
:
(1)有2个公共点?
(2)有1个公共点?
(3)有0个公共点?
解:
由方程组
①
②
代入②得
若Δ>0,即-25若Δ=0,即m=±25,此时方程由两个相等的实数根,即有1个公共点
若Δ<0,即m>25或m<-25,此时方程没有实根,即没有公共点
如何得到交点坐标?
进一步思考
这种方法能否用于判断其它曲线的关系呢?
如圆与椭圆,二次函数与椭圆,直线与多项式函数?
可以,步骤如下:
①列出两种曲线的方程
②联立,方程组的解就是交点坐标;方程组解的个数就是曲线交点个数
如三次函数
与直线
就是方程
的交点个数
的解的个数
三次方程有公式,但在此不赘述
由代数基本定理:n次方程最多有n个实数根,因此可以判断,直线和三次函数图像最多有3个交点
数形结合的思想
代数与几何本是两个不同的领域
代数是抽象而精确的,几何是形象的
坐标系的引入为几何图形建立了代数的描述
几何图形的问题,可以通过代数求解,得到精确的结论
一些代数问题,也可以转化为形象的几何问题,得到简单清晰的解答
小结
椭圆与直线关系
数形结合的思想:用代数解决几何问题
用几何给代数问题提供思路
再会!
3.1.2椭圆的简单几何性质
1、复习巩固
2、课堂探究
探究1:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点,为坐标原点. 探究:当在何位置时,最小?又在何位置时,最大?
设
则
因为
所以
所以
拓展1:已知椭圆,为椭圆上一动点,为坐标原点. 探究:当在何位置时,最小?又在何位置时,最大?
当在短轴顶点时,
当在长轴顶点时,
2、课堂探究
探究2:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点. 探究:当在何位置时,最小?又在何位置时,最大?
设
则
因为
所以
即
拓展2:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点. 探究:当在何位置时,最小?又在何位置时,最大?
设
则
因为
所以
即
椭圆,、分别为椭圆的左、右焦点,为椭圆上一动点.
, .
左准线
右准线
焦半径公式
3、课后巩固
动点与定点的距离和到定直线的距离的比是常数,求动点的轨迹.
4、课后探究
探究1:已知椭圆,、分别为椭圆的左、右焦点. 为椭圆上一动点. 探究:当在何位置时,最大?又在何位置时,最小?
4、课后探究
探究2:已知椭圆,、分别为椭圆的左、右顶点. 为椭圆上一动点. 探究:当在何位置时,最大?又在何位置时,最小?
5、课堂小结
椭圆,、分别为椭圆的左、右焦点,坐标原点,为椭圆上一动点.
(1)到左焦点的距离与它到左准线的距离的比为离心率,即 ,;
(2)到右焦点的距离与它到右准线的距离的比为离心率即,
(3), ;
(4), .
5、课堂小结
数学思想方法:
消元思想
从特殊到一般思想
数形结合思想
再会!
(第二课时)
3.1.2椭圆的简单几何性质
椭圆与直线的关系
直线和椭圆可以有哪些关系?
相交
相离
相切
给出解析式,如何判断是哪种情况?
相切、相交、相离的本质是什么?
交点个数:
1,2,0
问题化为求交点个数的问题
交点的本质是什么?
交点是同时满足两个曲线方程的点
交点个数=方程组解的个数
如何求方程组的解
代入!
①
②
①
②
怎么代入?
①化为
代入②
转变为:
关于的一元二次方程
一元二次方程的解有哪些情况?
无解
有两个相同的解
有两个不同的解
相离
相切
相离
来实战!
例题1:直线
和椭圆
解:
由方程组
①
②
代入②得
代入①,得到
的关系是?若有交点,求出交点坐标
化简得到
交点为
得到交点的纵坐标!
这就是交点的横坐标!
例题2已知直线
和椭圆
为何值时,直线
与椭圆
:
(1)有2个公共点?
(2)有1个公共点?
(3)有0个公共点?
解:
由方程组
①
②
代入②得
若Δ>0,即-25
若Δ<0,即m>25或m<-25,此时方程没有实根,即没有公共点
如何得到交点坐标?
进一步思考
这种方法能否用于判断其它曲线的关系呢?
如圆与椭圆,二次函数与椭圆,直线与多项式函数?
可以,步骤如下:
①列出两种曲线的方程
②联立,方程组的解就是交点坐标;方程组解的个数就是曲线交点个数
如三次函数
与直线
就是方程
的交点个数
的解的个数
三次方程有公式,但在此不赘述
由代数基本定理:n次方程最多有n个实数根,因此可以判断,直线和三次函数图像最多有3个交点
数形结合的思想
代数与几何本是两个不同的领域
代数是抽象而精确的,几何是形象的
坐标系的引入为几何图形建立了代数的描述
几何图形的问题,可以通过代数求解,得到精确的结论
一些代数问题,也可以转化为形象的几何问题,得到简单清晰的解答
小结
椭圆与直线关系
数形结合的思想:用代数解决几何问题
用几何给代数问题提供思路
再会!
