冀教版数学七年级下册 9.1三角形的边(1)课件(共24张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 9.1三角形的边(1)课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 17:31:18 | ||
图片预览







文档简介
(共24张PPT)
我 会 举 例 子
同学们,你能再举出一些生活中的三角形的例子吗?试一试!
说一说:
关于三角形,你都知道些什么?
自主学习课本第100-101页 观察与思考、大家谈谈的
内容,继续了解:
1、三角形的定义
2、三角形的顶点、边、内角
3、三角形的表示方法
4、三角形三边之间的关系及应用
5、三角形按边分类
1、三角形的定义
一、三角形的有关概念:
由不在同一条直线上的三条线段首尾顺次连接所构成的图形,叫做三角形。
所以,三角形的特征有:
(1)不在同一直线上
(2)三条线段
(3)首尾顺次连接(形成封闭图形)
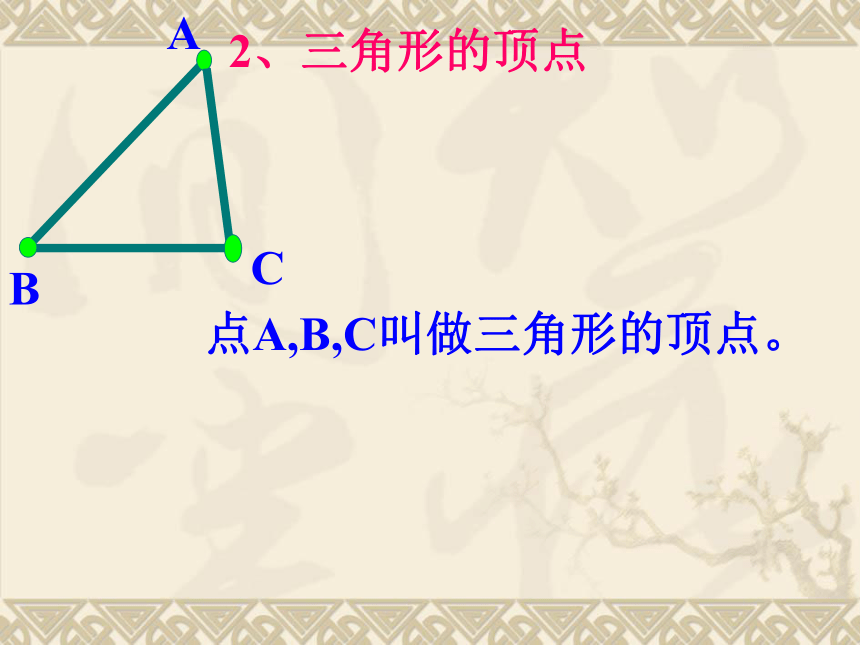
点A,B,C叫做三角形的顶点。
2、三角形的顶点
A
B
C
线段AB,BC,AC叫做三角形的边。
3、三角形的边
A
B
C
三角形ABC的三边,也可以用a、b、c来表示.一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c
a
b
c
4、三角形的角:
∠A, ∠ B, ∠ C叫做三角形的内角,简称三角形的角。
A
B
C
)
)
)
5、三角形的表示:
A
B
C
三角形用符号“△”表示
记作“△ ABC”读作“三角形ABC”
如图是用三根小棒组成的图形, 其中符合三角形定义的图形是( )
D
A
C
B
D
练一练:
二、探究三角形三边关系:
如图三角形中,假设有一只蚂蚁要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
路线1:由点B到点C
路线2:由点B到点A,再由点A到点C。
两条路线长分别是BC, AB+AC.
A
B
C
因为BC是线段
由“两点之间,线段最短”
可以得到AB+AC>BC
同理可得: AC+BC>AB,AB+BC>AC
家
学校
1
2
3
4
二、探究三角形三边关系:
1.用长10cm、10cm、20cm的小棒能组成三角形吗?
2、用8cm、10cm、20cm呢?
3、用10cm、20cm、15cm呢?
结论
三角形的三边有这样的关系:
三角形任意两边的和大于第三边。
大家谈一谈:
已知一个三角形的最小边为2cm,另两边分别为6cm和a cm , a的取值范围是什么?
结 论
三角形的三边有这样的关系:
1、三角形任意两边的和大于第三边。
2、 三角形任意两边的差小于第三边。
1.下列长度的三条线段能否组成三角形?
(1) 3,8,4
(2) 2,5,6
(3) 5,6,10
(4) 3,5,8
不能
能
能
不能
大
道
图 书 馆
教
学
楼
草坪
请勿
践踏!
2、尽管草地不允许踩,但还是被人们踩出了一条小路,这是
为什么?我们能不能运用今天所学的知识解释这一现象?
该走哪条路:
A
B
C
有两条边相等的三角形叫做等腰三角形。
三条边都相等的三角形叫做等边三角形。
等边三角形
不等边三角形
等边三角形也是等腰三角形吗?
腰
腰
底边
顶角
等腰三角形
不等边三角形
按边分类
等腰三角形
等边三角形(腰和底相等,又叫正三角形)
腰和底不相等的等腰三角形
三、三角形的分类
练一练
3. 已知一个等腰三角形的一条边等于6,一条边等于13,你会求它的周长吗?试一试,你一定能行的!
温馨提示:
要注意,你确定的底和腰三边的长能否围成三角形
1.三角形的定义;
2.三角形的顶点、边、角;
3.用符号表示三角形;
4.三角形三边关系及应用;
5.三角形按边分类.
谈一谈:你本节课收获了什么?
我 会 举 例 子
同学们,你能再举出一些生活中的三角形的例子吗?试一试!
说一说:
关于三角形,你都知道些什么?
自主学习课本第100-101页 观察与思考、大家谈谈的
内容,继续了解:
1、三角形的定义
2、三角形的顶点、边、内角
3、三角形的表示方法
4、三角形三边之间的关系及应用
5、三角形按边分类
1、三角形的定义
一、三角形的有关概念:
由不在同一条直线上的三条线段首尾顺次连接所构成的图形,叫做三角形。
所以,三角形的特征有:
(1)不在同一直线上
(2)三条线段
(3)首尾顺次连接(形成封闭图形)
点A,B,C叫做三角形的顶点。
2、三角形的顶点
A
B
C
线段AB,BC,AC叫做三角形的边。
3、三角形的边
A
B
C
三角形ABC的三边,也可以用a、b、c来表示.一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c
a
b
c
4、三角形的角:
∠A, ∠ B, ∠ C叫做三角形的内角,简称三角形的角。
A
B
C
)
)
)
5、三角形的表示:
A
B
C
三角形用符号“△”表示
记作“△ ABC”读作“三角形ABC”
如图是用三根小棒组成的图形, 其中符合三角形定义的图形是( )
D
A
C
B
D
练一练:
二、探究三角形三边关系:
如图三角形中,假设有一只蚂蚁要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
路线1:由点B到点C
路线2:由点B到点A,再由点A到点C。
两条路线长分别是BC, AB+AC.
A
B
C
因为BC是线段
由“两点之间,线段最短”
可以得到AB+AC>BC
同理可得: AC+BC>AB,AB+BC>AC
家
学校
1
2
3
4
二、探究三角形三边关系:
1.用长10cm、10cm、20cm的小棒能组成三角形吗?
2、用8cm、10cm、20cm呢?
3、用10cm、20cm、15cm呢?
结论
三角形的三边有这样的关系:
三角形任意两边的和大于第三边。
大家谈一谈:
已知一个三角形的最小边为2cm,另两边分别为6cm和a cm , a的取值范围是什么?
结 论
三角形的三边有这样的关系:
1、三角形任意两边的和大于第三边。
2、 三角形任意两边的差小于第三边。
1.下列长度的三条线段能否组成三角形?
(1) 3,8,4
(2) 2,5,6
(3) 5,6,10
(4) 3,5,8
不能
能
能
不能
大
道
图 书 馆
教
学
楼
草坪
请勿
践踏!
2、尽管草地不允许踩,但还是被人们踩出了一条小路,这是
为什么?我们能不能运用今天所学的知识解释这一现象?
该走哪条路:
A
B
C
有两条边相等的三角形叫做等腰三角形。
三条边都相等的三角形叫做等边三角形。
等边三角形
不等边三角形
等边三角形也是等腰三角形吗?
腰
腰
底边
顶角
等腰三角形
不等边三角形
按边分类
等腰三角形
等边三角形(腰和底相等,又叫正三角形)
腰和底不相等的等腰三角形
三、三角形的分类
练一练
3. 已知一个等腰三角形的一条边等于6,一条边等于13,你会求它的周长吗?试一试,你一定能行的!
温馨提示:
要注意,你确定的底和腰三边的长能否围成三角形
1.三角形的定义;
2.三角形的顶点、边、角;
3.用符号表示三角形;
4.三角形三边关系及应用;
5.三角形按边分类.
谈一谈:你本节课收获了什么?
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
