四边形综合测试卷一
图片预览
文档简介
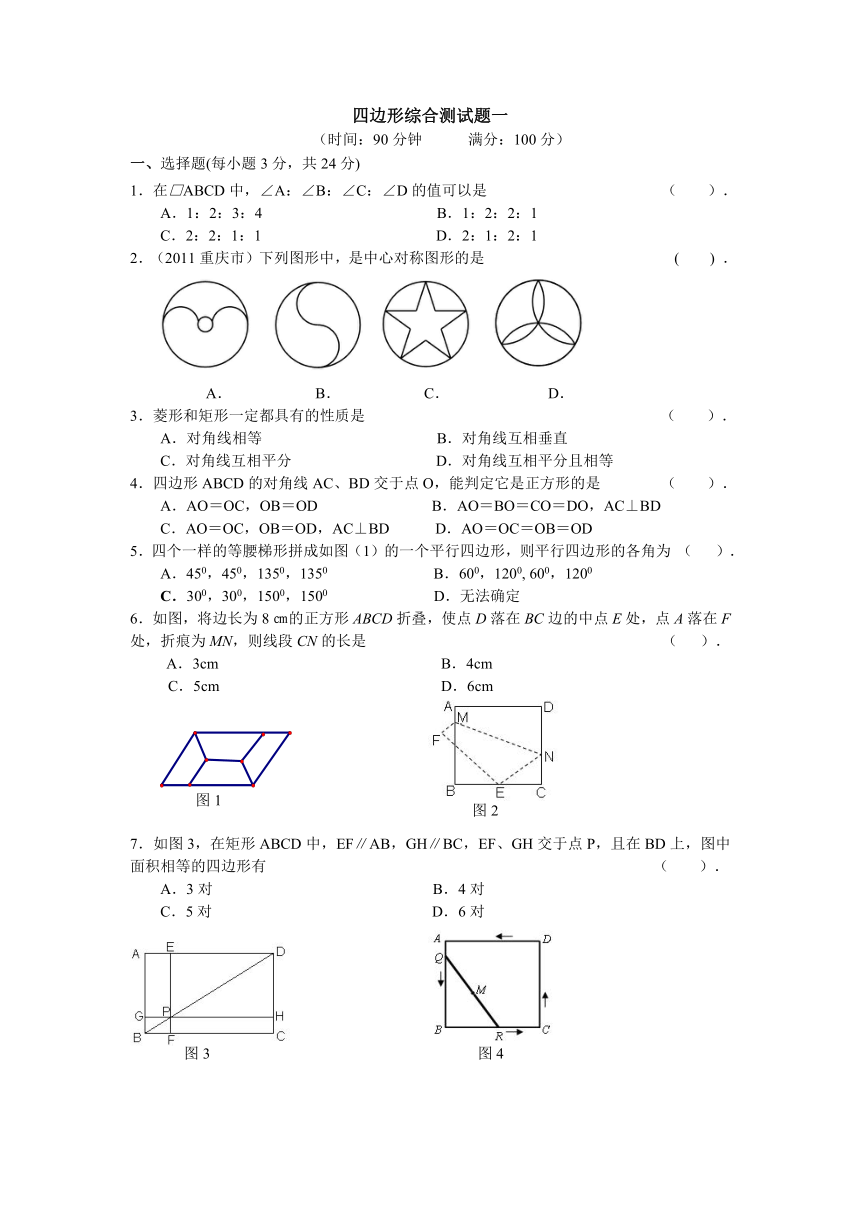
四边形综合测试题一
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.在□ABCD中,∠A:∠B:∠C:∠D的值可以是 ( ).
A.1:2:3:4 B.1:2:2:1
C.2:2:1:1 D.2:1:2:1
2.(2011重庆市)下列图形中,是中心对称图形的是 ( ) .
A. B. C. D.
3.菱形和矩形一定都具有的性质是 ( ).
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线互相平分且相等
4.四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是 ( ).
A.AO=OC,OB=OD B.AO=BO=CO=DO,AC⊥BD
C.AO=OC,OB=OD,AC⊥BD D.AO=OC=OB=OD
5.四个一样的等腰梯形拼成如图(1)的一个平行四边形,则平行四边形的各角为 ( ).
A.450,450,1350,1350 B.600,1200, 600,1200
C.300,300,1500,1500 D.无法确定
6.如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是 ( ).
A.3cm B.4cm
C.5cm D.6cm
7.如图3,在矩形ABCD中,EF∥AB,GH∥BC,EF、GH交于点P,且在BD上,图中面积相等的四边形有 ( ).
A.3对 B.4对
C.5对 D.6对
8.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为 ( ).
A.2 B.
C. D.
备:
1.下列矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是( B ).
2.多边形的一个顶点可以引9条对角线,那么这个多边形的内角和是 ( B ).
A. B.
C. D.
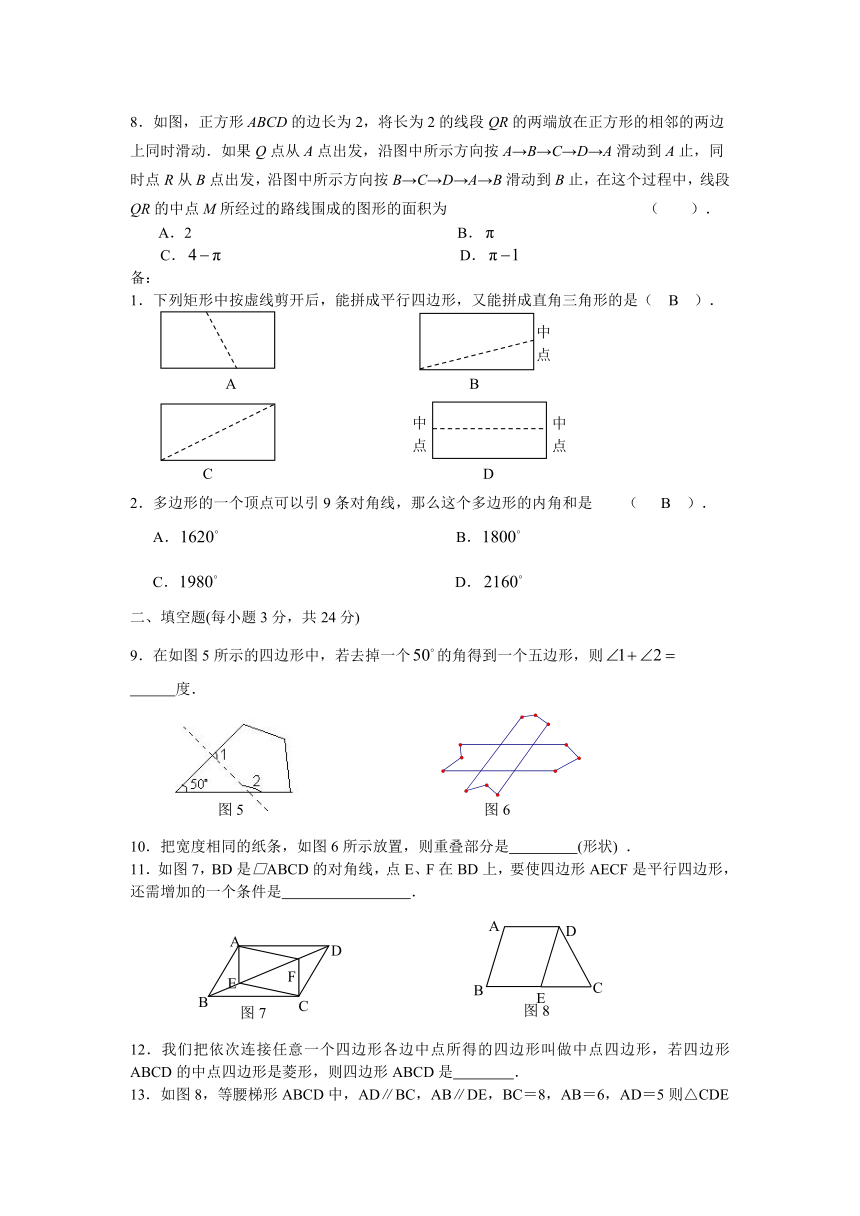
二、填空题(每小题3分,共24分)
9.在如图5所示的四边形中,若去掉一个的角得到一个五边形,则
度.
10.把宽度相同的纸条,如图6所示放置,则重叠部分是 (形状) .
11.如图7,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是 .
12.我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,若四边形ABCD的中点四边形是菱形,则四边形ABCD是 .
13.如图8,等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AB=6,AD=5则△CDE周长 .
14.(2011湖北鄂州)如图9:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为_______.
15.已知菱形的一条对角线长为12cm,面积为30cm2,则这个菱形的另一条对角线长为__________cm.
16.如图⑴,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍后得到正方形A2B2C2D2(如图⑵);以此下去…,则正方形A4B4C4D4的面积为 .
备:
1.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2, AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).①④
2.要从一张长为40cm,宽为20cm的矩形纸片中,剪出长为18cm,宽为12cm的矩形纸片,最多能剪出 张. 13
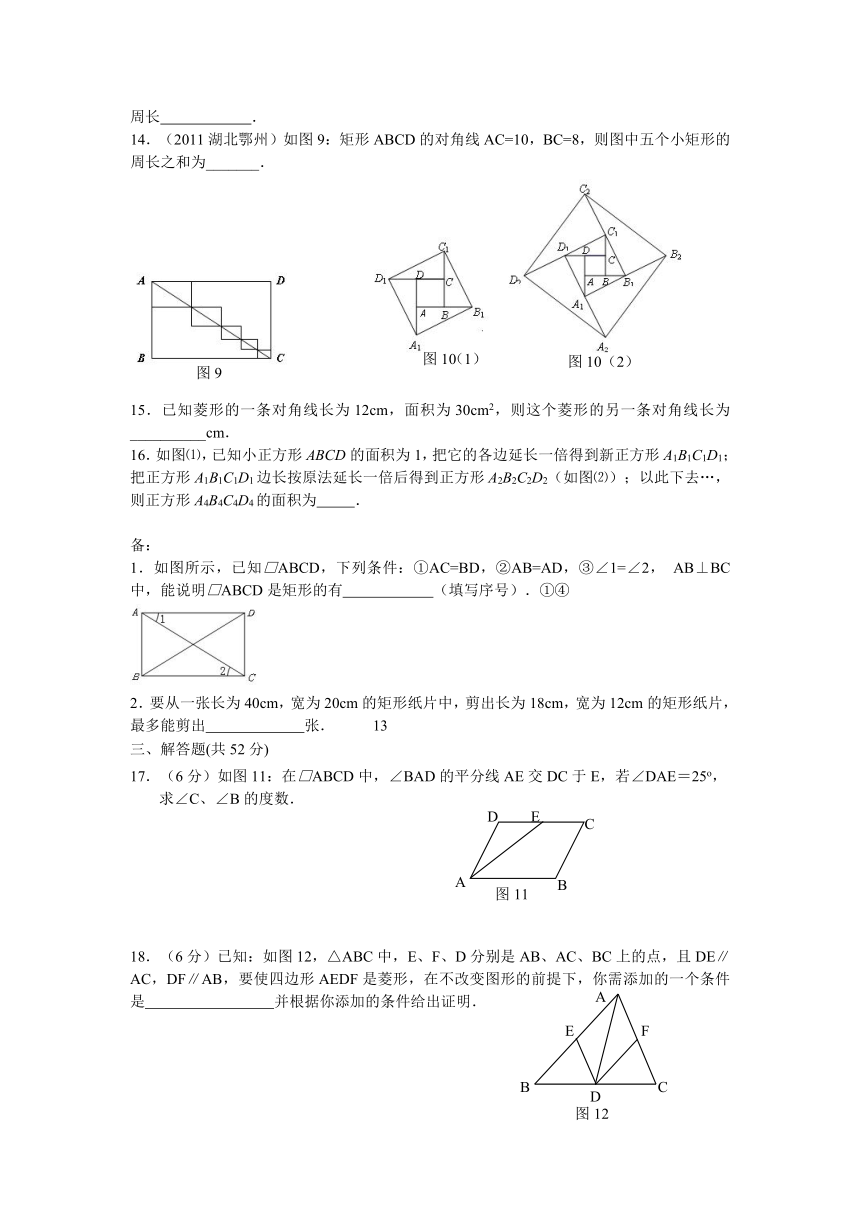
三、解答题(共52分)
17.(6分)如图11:在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25o,
求∠C、∠B的度数.
18.(6分)已知:如图12,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是 并根据你添加的条件给出证明.
19.(8分)如图13,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1) 求证:四边形AECF是平行四边形;
(2) 若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长 .
20.(10分)如图14,在四边形ABCD中,AD//BC,,,点E、F、M、N分别是AB、CD、BC、DA的中点,已知BC=8,MN=3,求EF的长
21.(10分)如图15,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.
22.(12分)如图16,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
备:
1.如图,已知,在ABCD中,AE=CF,M、N分别是DE、BF的中点.
求证:四边形MFNE是平行四边形.
证明:由平行四边形可知,AD=BC,∠DAE=∠BCF,又∵AE=CF,∴△DAE≌△BCF.
∴DE=BF,∠AED=∠CFB .又∵M、N分别是BE、DF的中点,∴ME=NF.
又由AB∥CD,得∠AED=∠EDC , ∴∠EDC=∠BFC , ∴ME∥NF.
∴四边形MFNE为平行四边形.
2.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)证明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF= BC,证明平行四边形EGFH是正方形.
【证明】(1)∵G,F分别是BE,BC的中点,
∴GF∥EC且GF= EC.
又∵H是EC的中点,EH= EC,
∴GF∥EH且GF=EH.∴四边形EGFH是平行四边形.
(2)∵G,H分别是BE,EC的中点,∴GH∥BC且GH= BC.又∵EF⊥BC且EF= BC,
∴EF⊥GH且EF=GH.∴平行四边形EGFH是正方形.
参考答案:
1.D. 2.B. 3.C. 4.B. 5.B. 6.C. 7.B. 8.C.
9.230. 10.菱形. 11.答案不唯一,如BE=DF. 12.(填写一种即可)矩形,正方形,等腰梯形等. 13.15. 14.28. 15.5. 16.625.
17. ∵AE平分∠BAD,∠DAE=25o,∴∠DAB=50o.
又∵四边形ABCD是平行四边形,∴∠C=∠DAB=50o.∠B=180o—50 o =130 o.
18.条件AE=AF(或AD平分∠BAC,等).
证明:∵DE∥AC, DF∥AB,∴四边形AEDF是平行四边形.
又AE=AF,∴四边形AEDF是菱形.
19.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,
∴AF=EC,∴四边形AECF是平行四边形.
(2)∵四边形AECF是,∴AE=CE,∴∠ACE=∠CAE,∵∠BAC=90°,∴∠BAE=∠90°-∠CAE,∠B=∠90°-∠ACE,∴∠BAE=∠B,∴AE=BE,∴BE=AE=CE=BC=5.
20.过N点分别作NG∥AB,NH∥CD,分别交BC于G、H点
则四边形ABGN与四边形DCHN是平行四边形.
∴AN=BG,DN=CH,∠1=,∠2=.
∴GH=BC-AD,∠GNH=900,
又∵点E、F、M、N分别是AB、CD、BC、DA的中点,
∴MN=,即GH=2MN=6.∴AD=BC-GH=2
∴EF=.
21.OM与ON垂直且相等.
理由:∵四边形ABCD是正方形,∴BC=CD,∠ABC=∠BCD.
∵CN⊥DM,∴∠CDM=∠BCN.∴△DCM≌△CBN(ASA).
∴CM=BN.在△OCM与△OBN中,OC=OB,∠OCM=∠OBN,
CM=BN,∴△OCM≌△OBN.∴OM=ON,∠COM=∠BON
又∵∠BOC=900,∴∠MON=900,即OM⊥ON.
22.(1)证明:∵MN∥BC,∴∠OEC=∠BCE.∵CE平分∠ACB,∴∠ACE=∠BCE.∴∠OEC=∠OCE,即OE=OC.同理,OF=OC.∴EO=FO.
(2)当点O运动到AC边的中点时,四边形AECF是矩形
∵由(1)知EO=FO,又∵OA=OC,∴四边形AECF是平行四边形.又由CE、CF分别平分∠ACB与∠ACB的外角,∴∠ECF=900.∴四边形AECF是矩形
(3)△ABC是直角三角形.由(2)知当O点是AC中点时,四边形AECF是矩形,当∠BCA=900时,∵MN∥BC,∴∠EOA=∠BCA=900.∴四边形AECF是正方形.
图1
图2
图3
图4
A
中
点
B
C
中
点
中
点
D
图5
图6
图7
D
A
B
C
E
F
D
A
B
C
E
图8
图9
图10(2)
图10(1)
D
C
A
B
E
图11
C
D
B
A
F
E
图12
图13
图14
A
B
N
M
C
D
O
图15
图16
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.在□ABCD中,∠A:∠B:∠C:∠D的值可以是 ( ).
A.1:2:3:4 B.1:2:2:1
C.2:2:1:1 D.2:1:2:1
2.(2011重庆市)下列图形中,是中心对称图形的是 ( ) .
A. B. C. D.
3.菱形和矩形一定都具有的性质是 ( ).
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线互相平分且相等
4.四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是 ( ).
A.AO=OC,OB=OD B.AO=BO=CO=DO,AC⊥BD
C.AO=OC,OB=OD,AC⊥BD D.AO=OC=OB=OD
5.四个一样的等腰梯形拼成如图(1)的一个平行四边形,则平行四边形的各角为 ( ).
A.450,450,1350,1350 B.600,1200, 600,1200
C.300,300,1500,1500 D.无法确定
6.如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是 ( ).
A.3cm B.4cm
C.5cm D.6cm
7.如图3,在矩形ABCD中,EF∥AB,GH∥BC,EF、GH交于点P,且在BD上,图中面积相等的四边形有 ( ).
A.3对 B.4对
C.5对 D.6对
8.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为 ( ).
A.2 B.
C. D.
备:
1.下列矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是( B ).
2.多边形的一个顶点可以引9条对角线,那么这个多边形的内角和是 ( B ).
A. B.
C. D.
二、填空题(每小题3分,共24分)
9.在如图5所示的四边形中,若去掉一个的角得到一个五边形,则
度.
10.把宽度相同的纸条,如图6所示放置,则重叠部分是 (形状) .
11.如图7,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是 .
12.我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,若四边形ABCD的中点四边形是菱形,则四边形ABCD是 .
13.如图8,等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AB=6,AD=5则△CDE周长 .
14.(2011湖北鄂州)如图9:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为_______.
15.已知菱形的一条对角线长为12cm,面积为30cm2,则这个菱形的另一条对角线长为__________cm.
16.如图⑴,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍后得到正方形A2B2C2D2(如图⑵);以此下去…,则正方形A4B4C4D4的面积为 .
备:
1.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2, AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).①④
2.要从一张长为40cm,宽为20cm的矩形纸片中,剪出长为18cm,宽为12cm的矩形纸片,最多能剪出 张. 13
三、解答题(共52分)
17.(6分)如图11:在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25o,
求∠C、∠B的度数.
18.(6分)已知:如图12,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是 并根据你添加的条件给出证明.
19.(8分)如图13,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1) 求证:四边形AECF是平行四边形;
(2) 若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长 .
20.(10分)如图14,在四边形ABCD中,AD//BC,,,点E、F、M、N分别是AB、CD、BC、DA的中点,已知BC=8,MN=3,求EF的长
21.(10分)如图15,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.
22.(12分)如图16,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
备:
1.如图,已知,在ABCD中,AE=CF,M、N分别是DE、BF的中点.
求证:四边形MFNE是平行四边形.
证明:由平行四边形可知,AD=BC,∠DAE=∠BCF,又∵AE=CF,∴△DAE≌△BCF.
∴DE=BF,∠AED=∠CFB .又∵M、N分别是BE、DF的中点,∴ME=NF.
又由AB∥CD,得∠AED=∠EDC , ∴∠EDC=∠BFC , ∴ME∥NF.
∴四边形MFNE为平行四边形.
2.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)证明四边形EGFH是平行四边形;
(2)在(1)的条件下,若EF⊥BC,且EF= BC,证明平行四边形EGFH是正方形.
【证明】(1)∵G,F分别是BE,BC的中点,
∴GF∥EC且GF= EC.
又∵H是EC的中点,EH= EC,
∴GF∥EH且GF=EH.∴四边形EGFH是平行四边形.
(2)∵G,H分别是BE,EC的中点,∴GH∥BC且GH= BC.又∵EF⊥BC且EF= BC,
∴EF⊥GH且EF=GH.∴平行四边形EGFH是正方形.
参考答案:
1.D. 2.B. 3.C. 4.B. 5.B. 6.C. 7.B. 8.C.
9.230. 10.菱形. 11.答案不唯一,如BE=DF. 12.(填写一种即可)矩形,正方形,等腰梯形等. 13.15. 14.28. 15.5. 16.625.
17. ∵AE平分∠BAD,∠DAE=25o,∴∠DAB=50o.
又∵四边形ABCD是平行四边形,∴∠C=∠DAB=50o.∠B=180o—50 o =130 o.
18.条件AE=AF(或AD平分∠BAC,等).
证明:∵DE∥AC, DF∥AB,∴四边形AEDF是平行四边形.
又AE=AF,∴四边形AEDF是菱形.
19.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,
∴AF=EC,∴四边形AECF是平行四边形.
(2)∵四边形AECF是,∴AE=CE,∴∠ACE=∠CAE,∵∠BAC=90°,∴∠BAE=∠90°-∠CAE,∠B=∠90°-∠ACE,∴∠BAE=∠B,∴AE=BE,∴BE=AE=CE=BC=5.
20.过N点分别作NG∥AB,NH∥CD,分别交BC于G、H点
则四边形ABGN与四边形DCHN是平行四边形.
∴AN=BG,DN=CH,∠1=,∠2=.
∴GH=BC-AD,∠GNH=900,
又∵点E、F、M、N分别是AB、CD、BC、DA的中点,
∴MN=,即GH=2MN=6.∴AD=BC-GH=2
∴EF=.
21.OM与ON垂直且相等.
理由:∵四边形ABCD是正方形,∴BC=CD,∠ABC=∠BCD.
∵CN⊥DM,∴∠CDM=∠BCN.∴△DCM≌△CBN(ASA).
∴CM=BN.在△OCM与△OBN中,OC=OB,∠OCM=∠OBN,
CM=BN,∴△OCM≌△OBN.∴OM=ON,∠COM=∠BON
又∵∠BOC=900,∴∠MON=900,即OM⊥ON.
22.(1)证明:∵MN∥BC,∴∠OEC=∠BCE.∵CE平分∠ACB,∴∠ACE=∠BCE.∴∠OEC=∠OCE,即OE=OC.同理,OF=OC.∴EO=FO.
(2)当点O运动到AC边的中点时,四边形AECF是矩形
∵由(1)知EO=FO,又∵OA=OC,∴四边形AECF是平行四边形.又由CE、CF分别平分∠ACB与∠ACB的外角,∴∠ECF=900.∴四边形AECF是矩形
(3)△ABC是直角三角形.由(2)知当O点是AC中点时,四边形AECF是矩形,当∠BCA=900时,∵MN∥BC,∴∠EOA=∠BCA=900.∴四边形AECF是正方形.
图1
图2
图3
图4
A
中
点
B
C
中
点
中
点
D
图5
图6
图7
D
A
B
C
E
F
D
A
B
C
E
图8
图9
图10(2)
图10(1)
D
C
A
B
E
图11
C
D
B
A
F
E
图12
图13
图14
A
B
N
M
C
D
O
图15
图16
