2012~2013学年度第二学期安徽省蚌埠市四边形综合测试卷二
文档属性
| 名称 | 2012~2013学年度第二学期安徽省蚌埠市四边形综合测试卷二 |  | |
| 格式 | zip | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-13 19:22:47 | ||
图片预览


文档简介
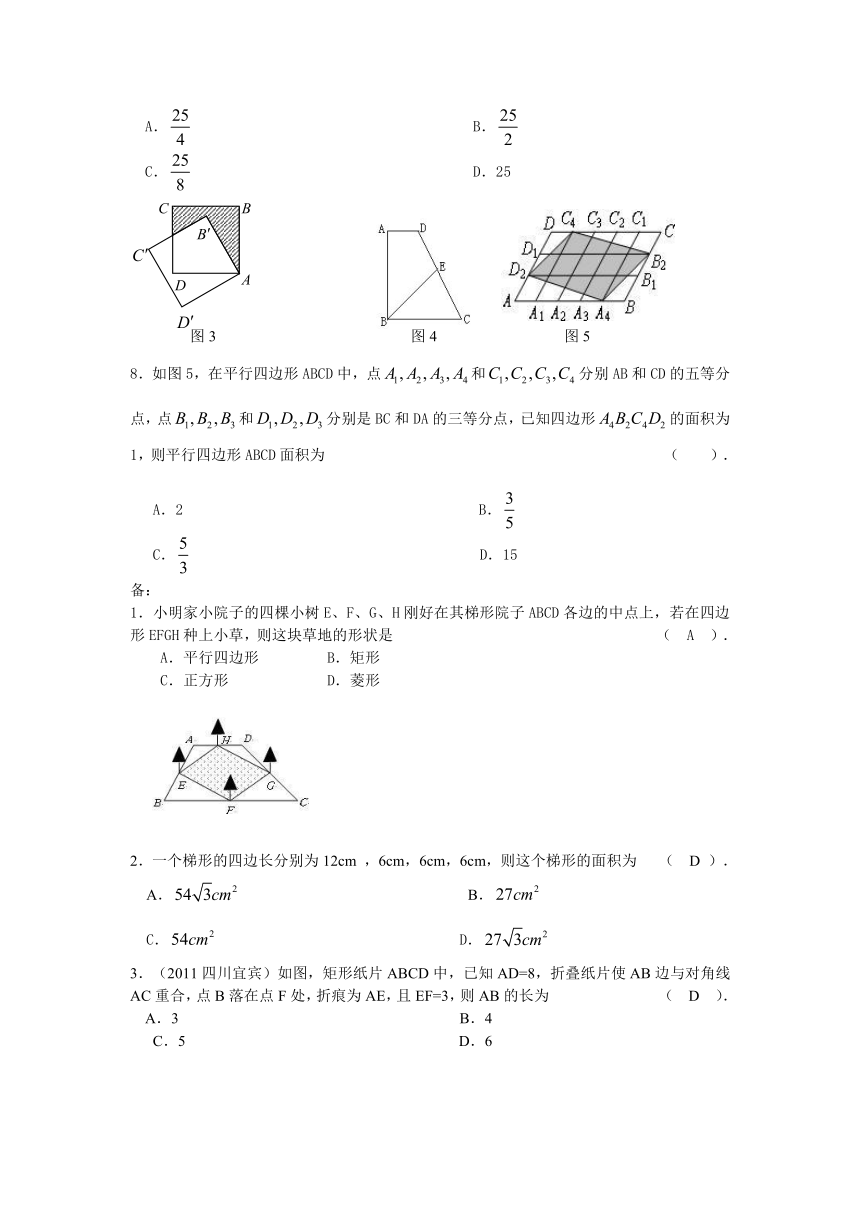
四边形综合测试题二
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.一个多边形的内角和是,则这个多边形是 ( ).
A.六边形 B.七边形
C.八边形 D.九边形
2.如图1,在中,已知AD=8cm ,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于 ( ).
A.2cm B.4cm
C.6cm D.8cm
3. (2011山东枣庄)下列图形中,既是轴对称图形,又是中心对称图形的是 ( ).
4.直角三角形中,两条直角边长分别是12和5,则斜边中线长为 ( ).
A.26 B.13
C. D.6.5
5.如图2,在矩形ABCD中,E,F分别在CD,AB上,AE⊥BD于M,CF⊥BD于N,则图中有全等三角形 ( ).
A.2对 B.3对
C.4对 D.5对
6.如图3,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为 ( ).
A. B.
C. D.
7.如图4,在直角梯形ABCD中,AD∥BC,点E是边CD的中点,若AB=AD+BC,BE=,则梯形ABCD的面积为 ( ).
A. B.
C. D.25
8.如图5,在平行四边形ABCD中,点和分别AB和CD的五等分点,点和分别是BC和DA的三等分点,已知四边形的面积为1,则平行四边形ABCD面积为 ( ).
A.2 B.
C. D.15
备:
1.小明家小院子的四棵小树E、F、G、H刚好在其梯形院子ABCD各边的中点上,若在四边形EFGH种上小草,则这块草地的形状是 ( A ).
A.平行四边形 B.矩形
C.正方形 D.菱形
2.一个梯形的四边长分别为12cm ,6cm,6cm,6cm,则这个梯形的面积为 ( D ).
A. B.
C. D.
3.(2011四川宜宾)如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 ( D ).
A.3 B.4
C.5 D.6
填空题(每小题3分,共24分)
9.如图6,菱形ABCD中,对角线AC、BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件是 (只填一个条件即可).
10.如图7,□ABCD中,BD为对角线,E、F分别为AD、BD的中点,连接EF,若EF=3,则CD的长为 .
11.正方形的边长为,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图8所示,则图中阴影部分的面积之和等于 .
12.在平行四边形、菱形、矩形、正方形、等腰梯形和直角梯形中,对角线相等的四边形有
.
13.如图9,□ABCD中,BE⊥AD于E,BF⊥CD于F,BE=2,BF=3,□ABCD的周长为20,□ABCD的面积为 .
14.(2011四川绵阳)如图10,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则折痕EF的长为_____cm.
15.如图11,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是 .
16.如图12,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP =EF;②AP⊥EF;③△APD一定是等腰三角形;
④∠PFE=∠BAP;⑤PD= EC.其中正确结论的序号是 .
备:
1.如图,在菱形ABCD中,∠A=600,E、F分别是AB、AD的中点,若EF=2,则菱形ABCD的边长是
2.已知点P为□ABCD内一点,,则 .
三、解答题(共52分)
17.(6分)已知,如图13,在□ABCD中,E、F是对角线BD上两点,且BF=DE,求证:AE=CF.
18.(8分)如图14,在菱形ABCD中,∠A=60°,=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1) 求∠ABD 的度数;
(2)求线段的长.
19.(8分)如图15, 在正方形ABCD中, M为AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.试说明:MD=MN.
20.(8分)如图16,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若AB=AC,求证:四边形BFCE是菱形.
21.(10分)已知:如图17,在直角梯形ABCD中,∠B=90o,AD∥BC,AD=24cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当其一点到端点时,另一点也随之停止运动,设运动时间为t秒,t分别为何值时,四边形PQCD是平行四边形?等腰梯形?
22. (12分)如图18,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)试探索四边形EGFH的形状,并说明理由;
(2)当E运动到什么位置时,四边形EGFH是菱形?并加以证明.
(3)若(2)中的菱形EGFH是正方形,请探索线段EF与线段BC的关系,并证明你的结论.
备:
1.如图,在四边形ABFC中,,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究四边形BECF是什么特殊四边形.
(2)当的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论
(1)四边形BECF是菱形,∵EF垂直平分BC,∴BF=FC,BE=EC,
∴∠ABC=∠BCE.∵∠ACB=90°,
∴∠ABC+∠A=90°,∠ACE+∠BCE=90°,
∴∠ACE=∠A,∴EC=AE.∴BE=AE,
∵CF=AE,∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.∵∠A=45°,∠ACB=90°,
∴∠ABC=45°,∴∠EBF=2∠A=90°,∴菱形BECF是正方形.
2.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(1)在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,∵AN是△ABC外角∠CAM的平分线,∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=×180°=90°.
又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.
(2)给出正确条件即可.
例如,当AD= BC时,四边形ADCE是正方形.
∵AB=AC,AD⊥BC于D,∴DC= BC,又∵AD= BC,∴DC=AD.
由(1)四边形ADCE为矩形,∴矩形ADCE是正方形.
参考答案:
1.C 2.A 3.B 4.D 5.D 6.C 7.A 8.C
9.答案不唯一,如AC=BD,∠ABC=900等 10.6 11.
12.矩形、正方形、等腰梯形 13.12 14. 15.17
16.①、②、④、⑤.
17.∵四边形ABCD是平行四边形,∴AD=CB,AD∥CB.∴∠ADE=∠CBF.
又∵DE=BF,∴△ADE≌△CBF.∴AE=CF.
18.(1)在菱形中,,,∴为等边三角形.
∴.
(2)由(1)可知,又∵为的中点,
∴. 又∵,及,∴.∴.
19.证明:取AD中点F,连接MF.
∵四边形ABCD是正方形,∴AD=AB,∠A=∠ABC=900.
∵点M、F是AB、AD的中点,∴DF=BM.
∵MN⊥MD,∴∠ADM=∠NME.
∵∠MBN=∠ABC+∠CBN=1350,∠DFM=1800—∠AFM=1350,
∴△DFM≌△MBN.∴MD=MN.
20.证明:(1)∵CE∥BF,∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,即BD=DC,∴△BDF≌△EDC;(AAS)
(2)∵AB=AC,∴△ABC是等腰三角形;
又∵BD=DC,∴AD⊥BC; 由(1)知:△BDF≌△EDC,则DE=DF,DB=DC;
∴BC、EF互相垂直平分;∴四边形BFCE是菱形.
21.解因为AD∥BC,所以,只要QC=PD,则四边形PQCD就是平行四边形,
此时有3t=24-t,解之,得t=6(秒).当t=6秒时,四边形PQCD平行四边形.
同理,只要PQ=CD,PD≠QC,四边形PQCD为等腰梯形.
过P、D分别作BC的垂线交BC于E、F,则
由等腰梯形的性质可知,EF=PD,QE=FC=26-24=2,
所以2,解得
所以当t=7秒时,四边形PQCD是等腰梯形.
22.解:(1)四边形EGFH为平行四边形.
∵G、F、H分别是BE、BC、CE的中点,∴FG、FH为△EBC的中位线,
∴FG∥EH,FH∥GE,∴EGFH为平行四边形.
(2)当点E运动到AD的中点时,四边形EGFH为菱形.
∵当点E运动到AD的中点时,AE=ED,又∠A=∠D,AB=CD,
∴△ABE≌△DCE(SAS).∴BE=CE,∴EG=EH,
即□EGFH为菱形.
(3)数量关系为,位置关系为:EF⊥BC.
当菱形EGFH是正方形时,∠BEC=900,∵F是BC中点,∴EF=BC.
∵EG=EH,∴BE=CE,即△BEC是等腰三角形,∴EF⊥BC.
图1
图2
A B C D
A
B
C
D
图3
图4
图5
图6
图7
图8
图9
图10
图11
图12
图13
图14
D
A
B
C
M
E
N
图15
图16
A
P
B
DD
Q
C
图17
图18
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.一个多边形的内角和是,则这个多边形是 ( ).
A.六边形 B.七边形
C.八边形 D.九边形
2.如图1,在中,已知AD=8cm ,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于 ( ).
A.2cm B.4cm
C.6cm D.8cm
3. (2011山东枣庄)下列图形中,既是轴对称图形,又是中心对称图形的是 ( ).
4.直角三角形中,两条直角边长分别是12和5,则斜边中线长为 ( ).
A.26 B.13
C. D.6.5
5.如图2,在矩形ABCD中,E,F分别在CD,AB上,AE⊥BD于M,CF⊥BD于N,则图中有全等三角形 ( ).
A.2对 B.3对
C.4对 D.5对
6.如图3,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为 ( ).
A. B.
C. D.
7.如图4,在直角梯形ABCD中,AD∥BC,点E是边CD的中点,若AB=AD+BC,BE=,则梯形ABCD的面积为 ( ).
A. B.
C. D.25
8.如图5,在平行四边形ABCD中,点和分别AB和CD的五等分点,点和分别是BC和DA的三等分点,已知四边形的面积为1,则平行四边形ABCD面积为 ( ).
A.2 B.
C. D.15
备:
1.小明家小院子的四棵小树E、F、G、H刚好在其梯形院子ABCD各边的中点上,若在四边形EFGH种上小草,则这块草地的形状是 ( A ).
A.平行四边形 B.矩形
C.正方形 D.菱形
2.一个梯形的四边长分别为12cm ,6cm,6cm,6cm,则这个梯形的面积为 ( D ).
A. B.
C. D.
3.(2011四川宜宾)如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 ( D ).
A.3 B.4
C.5 D.6
填空题(每小题3分,共24分)
9.如图6,菱形ABCD中,对角线AC、BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件是 (只填一个条件即可).
10.如图7,□ABCD中,BD为对角线,E、F分别为AD、BD的中点,连接EF,若EF=3,则CD的长为 .
11.正方形的边长为,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图8所示,则图中阴影部分的面积之和等于 .
12.在平行四边形、菱形、矩形、正方形、等腰梯形和直角梯形中,对角线相等的四边形有
.
13.如图9,□ABCD中,BE⊥AD于E,BF⊥CD于F,BE=2,BF=3,□ABCD的周长为20,□ABCD的面积为 .
14.(2011四川绵阳)如图10,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则折痕EF的长为_____cm.
15.如图11,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是 .
16.如图12,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP =EF;②AP⊥EF;③△APD一定是等腰三角形;
④∠PFE=∠BAP;⑤PD= EC.其中正确结论的序号是 .
备:
1.如图,在菱形ABCD中,∠A=600,E、F分别是AB、AD的中点,若EF=2,则菱形ABCD的边长是
2.已知点P为□ABCD内一点,,则 .
三、解答题(共52分)
17.(6分)已知,如图13,在□ABCD中,E、F是对角线BD上两点,且BF=DE,求证:AE=CF.
18.(8分)如图14,在菱形ABCD中,∠A=60°,=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1) 求∠ABD 的度数;
(2)求线段的长.
19.(8分)如图15, 在正方形ABCD中, M为AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.试说明:MD=MN.
20.(8分)如图16,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若AB=AC,求证:四边形BFCE是菱形.
21.(10分)已知:如图17,在直角梯形ABCD中,∠B=90o,AD∥BC,AD=24cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当其一点到端点时,另一点也随之停止运动,设运动时间为t秒,t分别为何值时,四边形PQCD是平行四边形?等腰梯形?
22. (12分)如图18,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)试探索四边形EGFH的形状,并说明理由;
(2)当E运动到什么位置时,四边形EGFH是菱形?并加以证明.
(3)若(2)中的菱形EGFH是正方形,请探索线段EF与线段BC的关系,并证明你的结论.
备:
1.如图,在四边形ABFC中,,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究四边形BECF是什么特殊四边形.
(2)当的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论
(1)四边形BECF是菱形,∵EF垂直平分BC,∴BF=FC,BE=EC,
∴∠ABC=∠BCE.∵∠ACB=90°,
∴∠ABC+∠A=90°,∠ACE+∠BCE=90°,
∴∠ACE=∠A,∴EC=AE.∴BE=AE,
∵CF=AE,∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.∵∠A=45°,∠ACB=90°,
∴∠ABC=45°,∴∠EBF=2∠A=90°,∴菱形BECF是正方形.
2.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(1)在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,∵AN是△ABC外角∠CAM的平分线,∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=×180°=90°.
又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.
(2)给出正确条件即可.
例如,当AD= BC时,四边形ADCE是正方形.
∵AB=AC,AD⊥BC于D,∴DC= BC,又∵AD= BC,∴DC=AD.
由(1)四边形ADCE为矩形,∴矩形ADCE是正方形.
参考答案:
1.C 2.A 3.B 4.D 5.D 6.C 7.A 8.C
9.答案不唯一,如AC=BD,∠ABC=900等 10.6 11.
12.矩形、正方形、等腰梯形 13.12 14. 15.17
16.①、②、④、⑤.
17.∵四边形ABCD是平行四边形,∴AD=CB,AD∥CB.∴∠ADE=∠CBF.
又∵DE=BF,∴△ADE≌△CBF.∴AE=CF.
18.(1)在菱形中,,,∴为等边三角形.
∴.
(2)由(1)可知,又∵为的中点,
∴. 又∵,及,∴.∴.
19.证明:取AD中点F,连接MF.
∵四边形ABCD是正方形,∴AD=AB,∠A=∠ABC=900.
∵点M、F是AB、AD的中点,∴DF=BM.
∵MN⊥MD,∴∠ADM=∠NME.
∵∠MBN=∠ABC+∠CBN=1350,∠DFM=1800—∠AFM=1350,
∴△DFM≌△MBN.∴MD=MN.
20.证明:(1)∵CE∥BF,∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,即BD=DC,∴△BDF≌△EDC;(AAS)
(2)∵AB=AC,∴△ABC是等腰三角形;
又∵BD=DC,∴AD⊥BC; 由(1)知:△BDF≌△EDC,则DE=DF,DB=DC;
∴BC、EF互相垂直平分;∴四边形BFCE是菱形.
21.解因为AD∥BC,所以,只要QC=PD,则四边形PQCD就是平行四边形,
此时有3t=24-t,解之,得t=6(秒).当t=6秒时,四边形PQCD平行四边形.
同理,只要PQ=CD,PD≠QC,四边形PQCD为等腰梯形.
过P、D分别作BC的垂线交BC于E、F,则
由等腰梯形的性质可知,EF=PD,QE=FC=26-24=2,
所以2,解得
所以当t=7秒时,四边形PQCD是等腰梯形.
22.解:(1)四边形EGFH为平行四边形.
∵G、F、H分别是BE、BC、CE的中点,∴FG、FH为△EBC的中位线,
∴FG∥EH,FH∥GE,∴EGFH为平行四边形.
(2)当点E运动到AD的中点时,四边形EGFH为菱形.
∵当点E运动到AD的中点时,AE=ED,又∠A=∠D,AB=CD,
∴△ABE≌△DCE(SAS).∴BE=CE,∴EG=EH,
即□EGFH为菱形.
(3)数量关系为,位置关系为:EF⊥BC.
当菱形EGFH是正方形时,∠BEC=900,∵F是BC中点,∴EF=BC.
∵EG=EH,∴BE=CE,即△BEC是等腰三角形,∴EF⊥BC.
图1
图2
A B C D
A
B
C
D
图3
图4
图5
图6
图7
图8
图9
图10
图11
图12
图13
图14
D
A
B
C
M
E
N
图15
图16
A
P
B
DD
Q
C
图17
图18
