湘教版数学七年级下册 5.3 图形变换的简单应用课件(共15张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 5.3 图形变换的简单应用课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 470.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 10:53:29 | ||
图片预览



文档简介
(共16张PPT)
第5章 轴对称与旋转
5.3 图形变化的简单应用
湘教版 七年级下册
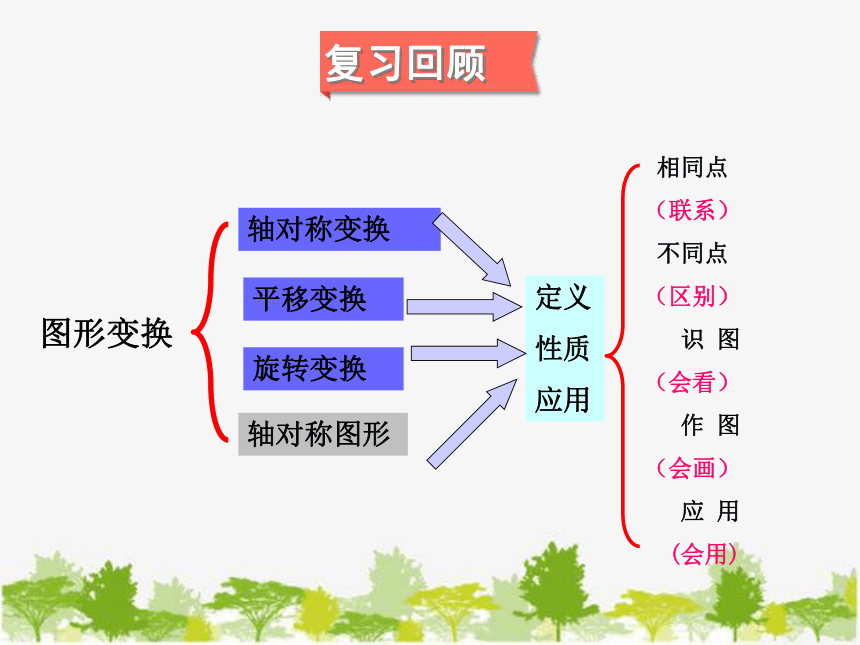
图形变换
平移变换
旋转变换
轴对称变换
轴对称图形
相同点
(联系)
不同点
(区别)
识 图
(会看)
作 图
(会画)
应 用
(会用)
定义
性质
应用
复习回顾
1、什么是轴对称变换、平移变换、旋转变换?
轴对称变换:由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫反射变换,简称反射.
平移变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移。
旋转变换 :由一个图形改变为另一个图形,在改变的过程中,原图形上的所有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形改变叫做图形的旋转变换,简称旋转.这个定点称为旋转中心,转动的角称为旋转角。
2、轴对称变换、平移变换、旋转变换的性质
共同点 不同点
轴对称变换
不改变图形的形状和大小 对应点的连线段被对称轴垂直平分
平移变换 两组对应点的连线平行(或在同一直线上)且相等。
旋转变换 对应点到旋转中心的距离相等;
两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角
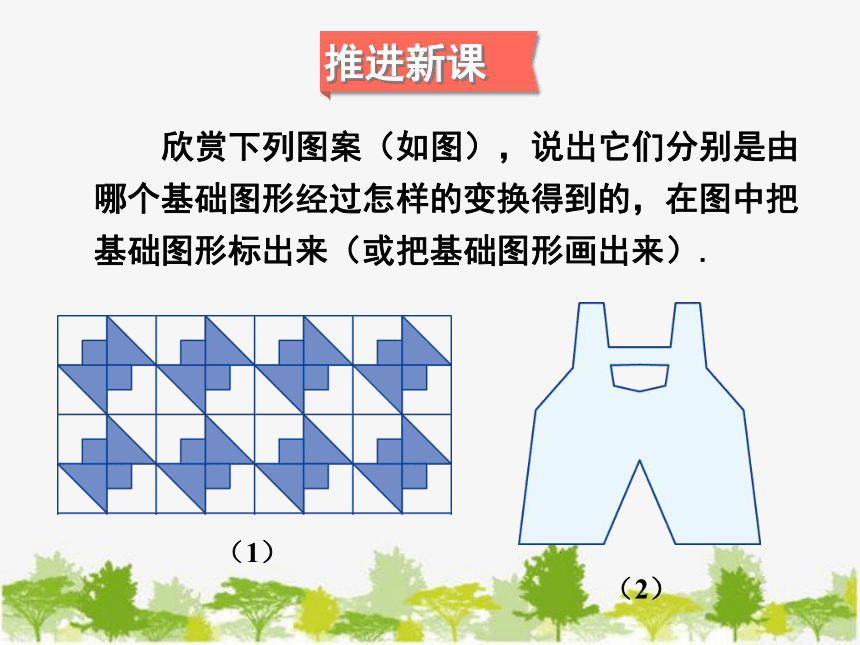
欣赏下列图案(如图),说出它们分别是由哪个基础图形经过怎样的变换得到的,在图中把基础图形标出来(或把基础图形画出来).
推进新课
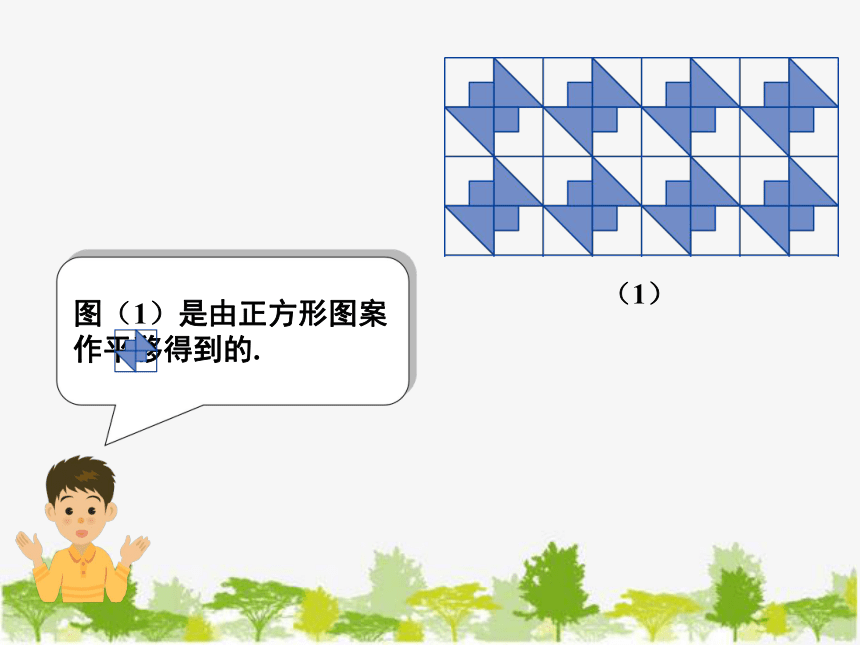
(1)
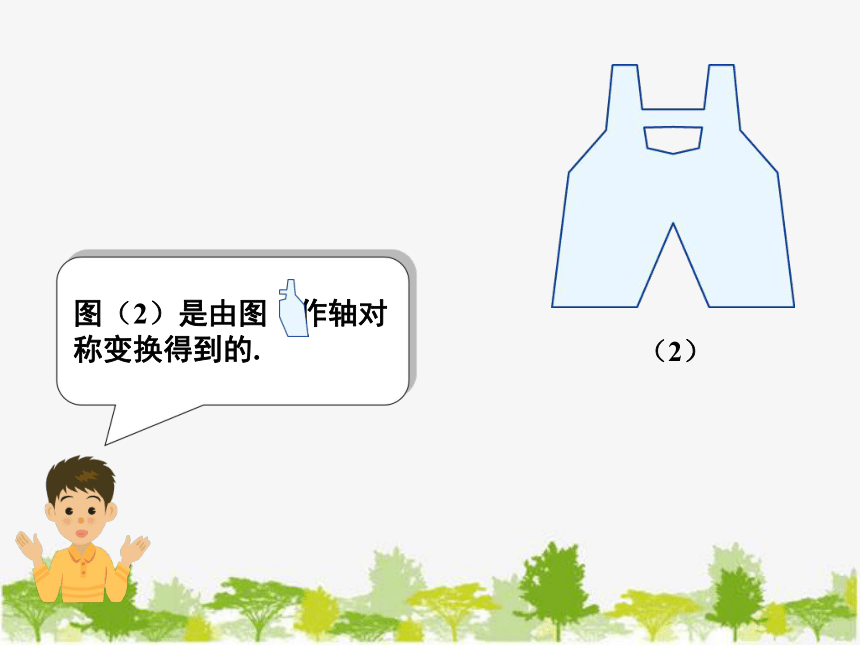
(2)
图(1)是由正方形图案 作平移得到的.
(1)
图(2)是由图 作轴对称变换得到的.
(2)
例1 以图的右边缘所在的直线为轴,将该图形向右作轴对称变换,再绕中心 O 按顺时针方向旋转180°,所得到的图形是( )
典例精析
分析 将图以右边缘所在的直线为轴作轴对称变换,得到图 ,再绕中心O按顺时针方向旋转180°,得到图 .
下图是一种正方形的瓷砖.
(1)请用4块所给瓷砖拼一个正方形图案(至少
设计3种不同的图案);
(2)如果给你16块这样的正方形瓷砖,要求设计
的图案为轴对称图形,你可以设计出来吗?
例2
下图中只能用其中一部分平移可以得到的是( ).
轴对称、平移不改变图形的形状和大小.平移前后图形对应点连线平行且相等,故选B.
解
B
D
A
B
C
例3
圆弧与扇形的对称轴是过弧中点和圆心的直线.角的对称轴是角平分线所在的直线.菱形和等腰梯形是轴对称图形.
解
如图,下列几何图形中,一定是轴对称图形的有( ).
A.2个 B.3个 C.4个 D.5个
D
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
读书,始读,未知有疑;其次,则渐渐有疑;中则节节是疑。过了这一番,疑渐渐释,以至融会贯通,都无所疑,方始是学。——朱熹
第5章 轴对称与旋转
5.3 图形变化的简单应用
湘教版 七年级下册
图形变换
平移变换
旋转变换
轴对称变换
轴对称图形
相同点
(联系)
不同点
(区别)
识 图
(会看)
作 图
(会画)
应 用
(会用)
定义
性质
应用
复习回顾
1、什么是轴对称变换、平移变换、旋转变换?
轴对称变换:由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫反射变换,简称反射.
平移变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移。
旋转变换 :由一个图形改变为另一个图形,在改变的过程中,原图形上的所有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形改变叫做图形的旋转变换,简称旋转.这个定点称为旋转中心,转动的角称为旋转角。
2、轴对称变换、平移变换、旋转变换的性质
共同点 不同点
轴对称变换
不改变图形的形状和大小 对应点的连线段被对称轴垂直平分
平移变换 两组对应点的连线平行(或在同一直线上)且相等。
旋转变换 对应点到旋转中心的距离相等;
两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角
欣赏下列图案(如图),说出它们分别是由哪个基础图形经过怎样的变换得到的,在图中把基础图形标出来(或把基础图形画出来).
推进新课
(1)
(2)
图(1)是由正方形图案 作平移得到的.
(1)
图(2)是由图 作轴对称变换得到的.
(2)
例1 以图的右边缘所在的直线为轴,将该图形向右作轴对称变换,再绕中心 O 按顺时针方向旋转180°,所得到的图形是( )
典例精析
分析 将图以右边缘所在的直线为轴作轴对称变换,得到图 ,再绕中心O按顺时针方向旋转180°,得到图 .
下图是一种正方形的瓷砖.
(1)请用4块所给瓷砖拼一个正方形图案(至少
设计3种不同的图案);
(2)如果给你16块这样的正方形瓷砖,要求设计
的图案为轴对称图形,你可以设计出来吗?
例2
下图中只能用其中一部分平移可以得到的是( ).
轴对称、平移不改变图形的形状和大小.平移前后图形对应点连线平行且相等,故选B.
解
B
D
A
B
C
例3
圆弧与扇形的对称轴是过弧中点和圆心的直线.角的对称轴是角平分线所在的直线.菱形和等腰梯形是轴对称图形.
解
如图,下列几何图形中,一定是轴对称图形的有( ).
A.2个 B.3个 C.4个 D.5个
D
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
读书,始读,未知有疑;其次,则渐渐有疑;中则节节是疑。过了这一番,疑渐渐释,以至融会贯通,都无所疑,方始是学。——朱熹
