四川省成都市金牛区重点中学2021-2022学年高二下学期期中考试数学文科试题(Word版含答案)
文档属性
| 名称 | 四川省成都市金牛区重点中学2021-2022学年高二下学期期中考试数学文科试题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 578.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览



文档简介
金牛区重点中学2021-2022学年高二下学期期中考试
数学试卷(文科)
一、选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求.把答案涂在答题卷上.)
1.复数的模( ).
A. B. C. D.
2.已知函数,则( ).
A. B. C. D.
3.对于不等式,某同学用数学归纳法证明的过程如下:
①当时,,不等式成立;
②假设当时,不等式成立,即,
则当时,
.
故当时,不等式成立.
则下列说法正确的是( ).
A.过程全部正确 B.当时的验证不正确
C.当时的归纳假设不正确 D.从到的推理不正确
4.有一段演绎推理:所有的质数是奇数,2是质数,所以2是奇数.这段推理( ).
A.大前提错误 B.小前提错误
C.推理形式错误 D.是正确的
5.函数在R上是( ).
A.偶函数、增函数 B.奇函数、减函数
C.偶函数、减函数 D.奇函数、增函数
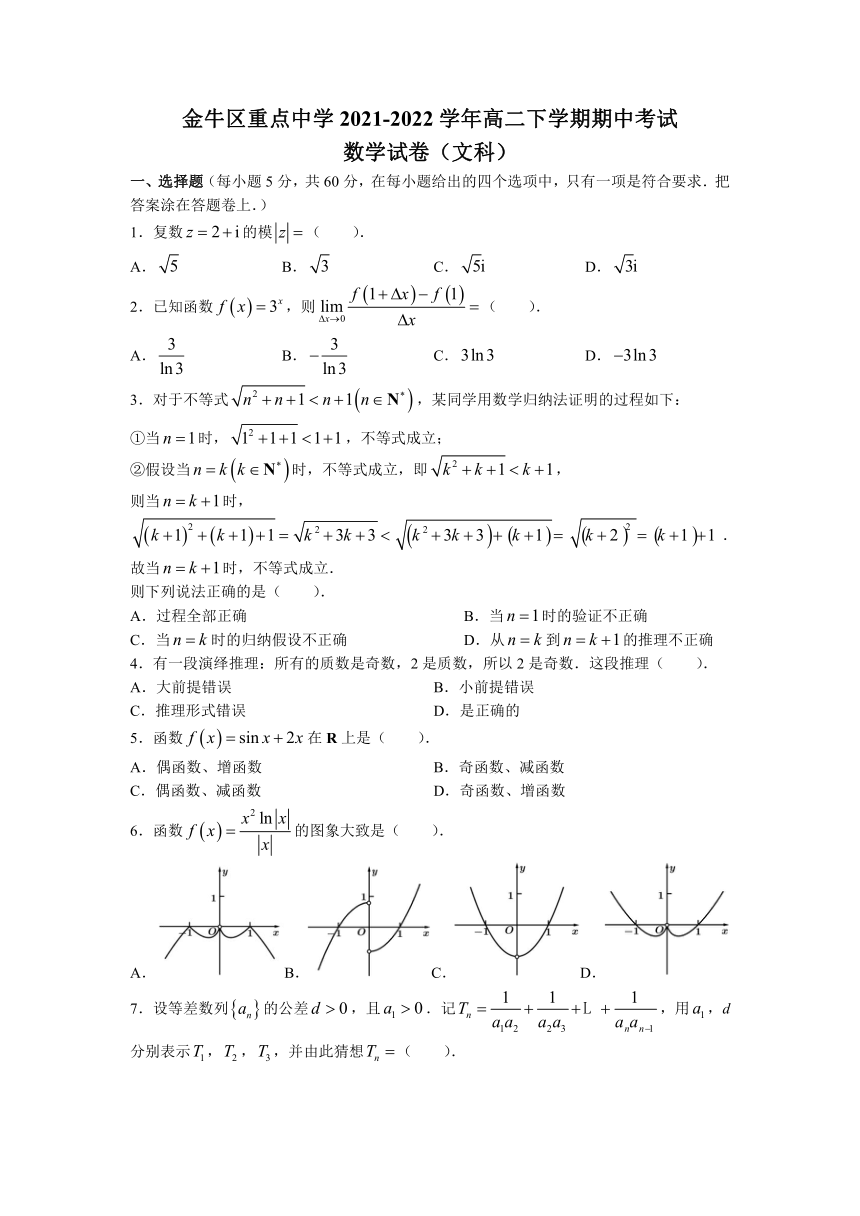
6.函数的图象大致是( ).
A.B.C.D.
7.设等差数列的公差,且.记,用,d分别表示,,,并由此猜想( ).
A. B. C. D.
8.已知函数,若,则实数a的取值范围是( ).
A. B.
C. D.
9.已知三棱锥中,,,,,E,F分别为棱CD,AB的中点,则直线EF与AC所成角的余弦值为( ).
A. B. C. D.
10.各种不同的进制在我们生活中随处可见,计算机使用的是二进制,数学运算一般用的十进制.通常我们用函数表示在x进制下表达个数字的效率,则下列选项中表达M个数字的效率最高的是( ).
A.四进制 B.三进制 C.八进制 D.七进制
11.我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.“鳖臑”指的是四个面都是直角三角形的三棱锥.“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以恭,其形露矣.”现有一如图所示的“堑堵”即三棱柱,其中,若,当“阳马”即四棱锥体积最大时,“堑堵”即三棱柱的外接球的表面积为( ).
A. B. C. D.
12.已知是定义在的减函数.设,,,则a,b,c的大小关系为( ).
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上.)
13.已知函数,则在点处的切线的斜率k=______.
14.如图,正方体的棱长为1,则点A到平面的距离是_______.
15.历史上数列折射出很多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多·斐波那契以兔子繁殖为例,引入“兔子数列”,即1,1,2,3,5,8,13,21,34,55,89,144,…,它满足,且满足递推关系,此数列在现代物理及化学等领域有着广泛的应用,若将此数列的每一项除以4后的余数构成一个新数列,______.
16.若对,关于x的不等式恒成立,则整数m的最小值为______.
三、解答题(17题10分,18-22每小题12分,共70分.在答题卷上解答,解答应写出文字说明,证明过程或演算步骤.)
17.已知复数.
(1)若对应复平面上的点在第四象限,求m的范围;
(2)当时,且(表示的共轭复数),若,求z.
18.已知数列,为数列的前n项和.
(1)求,,,;
(2)根据(1)的计算结果,猜想的表达式,并用数学归纳法进行证明.
19.如图,在长方体中,点E,F分别在,上,且,.
(1)证明:;
(2)当,,时,求三棱锥的体积.
20.第31届世界大学生夏季运动会即将在成都拉开帷幕.为了配合大运会的基础设施建设,组委会拟在成都东安湖体育公园修建一座具有成都文化特色的桥.两端的桥墩已建好,这两桥墩相距160米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米(其中,)的相邻两墩之间的桥面工程费用为万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,设需要新建n个桥墩(显然),记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)需新建多少个桥墩才能使y最小?
21.函数.
(1)若,对一切恒成立,求a的最大值;
(2)证明:,其中e是自然对数的底数.
22.设函数.
(1)当时,判断函数在上的单调性;
(2)设,且,当时,判断在的极值点个数.
金牛区重点中学2021-2022学年高二下学期期中考试
数学试卷(文科)(参考答案)
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A C D A D D C A D B D B
二、填空题
13. 14. 15.1 16.2
三、解答题
17.解:(1)若对应复平面上的点在第四象限,则,
解得.
(2)当时,,则.
∴,
∴.
18.解:(1),,
,.
(2)猜想:.
证明:①当时,左边,右边,等式成立.
②假设当时,等式成立,
即.
则当时,
左边
右边,
所以当时,等式成立,
由①②可知对于任意的时,
.
19.解:(1)证明:法一
由长方体性质可知,平面,∴,
又∵,,∴平面,
又平面,∴.同理可证,
又,∴平面AEF,又平面AEF,所以.
法二:因为,所以.
因为,所以.
,所以.
(2)∵,在面中,∽,
∴,可得,∴,.
20.解:(1)由,得,
所以
.
(2)由(1)知,,
令,得,所以.
当时,,则在区间内为减函数;
当时,,则在区间内为增函数.
所以在处取得最小值,此时.
故需新建9个桥墩才能使y最小.
21.解:(1),又,①当,恒成立,满足题意;
②当,令,,当,,单调递减,
当,,单调递增;
所以在处取得极小值,即最小值.要使恒成立,即,
代入得,解得.
综上,∴a的最大值为1.(也可参变分离)
(2)当时,由(1)可知,当且仅当成立.
令,即.
∴,,…,.相乘可得即证.
22.解:(1).
当时,,当时,.
∴当时,,当时,,
∴在单调递增,在单调递减.
(2)令,则,即.
设,则.
①当时,,,
令,则,
令,则,
从而,所以单调递减.又,,
由零点存在定理可知存在唯一,使得.
所以当时,,则单调递增,
当时,,则单调递减;又,,
所以由零点存在定理可知存在唯一,使得.
即.当时,,则单调递减,
当时,,则单调递增;
②当时,,则单调递减.
综上,在上单调递减,上单调递减,在上单调递增.
因为,则,即.
从而.
由①的唯一性可知,,则.
当时,;当时,.
当时,直线与函数的图象在上有两个交点,
从而有两个变号零点,即在上恰有两个极值点.
所以在上恰有两个极值点.
数学试卷(文科)
一、选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求.把答案涂在答题卷上.)
1.复数的模( ).
A. B. C. D.
2.已知函数,则( ).
A. B. C. D.
3.对于不等式,某同学用数学归纳法证明的过程如下:
①当时,,不等式成立;
②假设当时,不等式成立,即,
则当时,
.
故当时,不等式成立.
则下列说法正确的是( ).
A.过程全部正确 B.当时的验证不正确
C.当时的归纳假设不正确 D.从到的推理不正确
4.有一段演绎推理:所有的质数是奇数,2是质数,所以2是奇数.这段推理( ).
A.大前提错误 B.小前提错误
C.推理形式错误 D.是正确的
5.函数在R上是( ).
A.偶函数、增函数 B.奇函数、减函数
C.偶函数、减函数 D.奇函数、增函数
6.函数的图象大致是( ).
A.B.C.D.
7.设等差数列的公差,且.记,用,d分别表示,,,并由此猜想( ).
A. B. C. D.
8.已知函数,若,则实数a的取值范围是( ).
A. B.
C. D.
9.已知三棱锥中,,,,,E,F分别为棱CD,AB的中点,则直线EF与AC所成角的余弦值为( ).
A. B. C. D.
10.各种不同的进制在我们生活中随处可见,计算机使用的是二进制,数学运算一般用的十进制.通常我们用函数表示在x进制下表达个数字的效率,则下列选项中表达M个数字的效率最高的是( ).
A.四进制 B.三进制 C.八进制 D.七进制
11.我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.“鳖臑”指的是四个面都是直角三角形的三棱锥.“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以恭,其形露矣.”现有一如图所示的“堑堵”即三棱柱,其中,若,当“阳马”即四棱锥体积最大时,“堑堵”即三棱柱的外接球的表面积为( ).
A. B. C. D.
12.已知是定义在的减函数.设,,,则a,b,c的大小关系为( ).
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上.)
13.已知函数,则在点处的切线的斜率k=______.
14.如图,正方体的棱长为1,则点A到平面的距离是_______.
15.历史上数列折射出很多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多·斐波那契以兔子繁殖为例,引入“兔子数列”,即1,1,2,3,5,8,13,21,34,55,89,144,…,它满足,且满足递推关系,此数列在现代物理及化学等领域有着广泛的应用,若将此数列的每一项除以4后的余数构成一个新数列,______.
16.若对,关于x的不等式恒成立,则整数m的最小值为______.
三、解答题(17题10分,18-22每小题12分,共70分.在答题卷上解答,解答应写出文字说明,证明过程或演算步骤.)
17.已知复数.
(1)若对应复平面上的点在第四象限,求m的范围;
(2)当时,且(表示的共轭复数),若,求z.
18.已知数列,为数列的前n项和.
(1)求,,,;
(2)根据(1)的计算结果,猜想的表达式,并用数学归纳法进行证明.
19.如图,在长方体中,点E,F分别在,上,且,.
(1)证明:;
(2)当,,时,求三棱锥的体积.
20.第31届世界大学生夏季运动会即将在成都拉开帷幕.为了配合大运会的基础设施建设,组委会拟在成都东安湖体育公园修建一座具有成都文化特色的桥.两端的桥墩已建好,这两桥墩相距160米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米(其中,)的相邻两墩之间的桥面工程费用为万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,设需要新建n个桥墩(显然),记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)需新建多少个桥墩才能使y最小?
21.函数.
(1)若,对一切恒成立,求a的最大值;
(2)证明:,其中e是自然对数的底数.
22.设函数.
(1)当时,判断函数在上的单调性;
(2)设,且,当时,判断在的极值点个数.
金牛区重点中学2021-2022学年高二下学期期中考试
数学试卷(文科)(参考答案)
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A C D A D D C A D B D B
二、填空题
13. 14. 15.1 16.2
三、解答题
17.解:(1)若对应复平面上的点在第四象限,则,
解得.
(2)当时,,则.
∴,
∴.
18.解:(1),,
,.
(2)猜想:.
证明:①当时,左边,右边,等式成立.
②假设当时,等式成立,
即.
则当时,
左边
右边,
所以当时,等式成立,
由①②可知对于任意的时,
.
19.解:(1)证明:法一
由长方体性质可知,平面,∴,
又∵,,∴平面,
又平面,∴.同理可证,
又,∴平面AEF,又平面AEF,所以.
法二:因为,所以.
因为,所以.
,所以.
(2)∵,在面中,∽,
∴,可得,∴,.
20.解:(1)由,得,
所以
.
(2)由(1)知,,
令,得,所以.
当时,,则在区间内为减函数;
当时,,则在区间内为增函数.
所以在处取得最小值,此时.
故需新建9个桥墩才能使y最小.
21.解:(1),又,①当,恒成立,满足题意;
②当,令,,当,,单调递减,
当,,单调递增;
所以在处取得极小值,即最小值.要使恒成立,即,
代入得,解得.
综上,∴a的最大值为1.(也可参变分离)
(2)当时,由(1)可知,当且仅当成立.
令,即.
∴,,…,.相乘可得即证.
22.解:(1).
当时,,当时,.
∴当时,,当时,,
∴在单调递增,在单调递减.
(2)令,则,即.
设,则.
①当时,,,
令,则,
令,则,
从而,所以单调递减.又,,
由零点存在定理可知存在唯一,使得.
所以当时,,则单调递增,
当时,,则单调递减;又,,
所以由零点存在定理可知存在唯一,使得.
即.当时,,则单调递减,
当时,,则单调递增;
②当时,,则单调递减.
综上,在上单调递减,上单调递减,在上单调递增.
因为,则,即.
从而.
由①的唯一性可知,,则.
当时,;当时,.
当时,直线与函数的图象在上有两个交点,
从而有两个变号零点,即在上恰有两个极值点.
所以在上恰有两个极值点.
同课章节目录
