3.3.1两条直线的交点坐标(丁海燕)
文档属性
| 名称 | 3.3.1两条直线的交点坐标(丁海燕) |

|
|
| 格式 | zip | ||
| 文件大小 | 550.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-13 21:47:40 | ||
图片预览





文档简介
课件18张PPT。我国著名数学家华罗庚曾说过:数缺形时少直观,
形少数时难入微;
数形结合百般好,
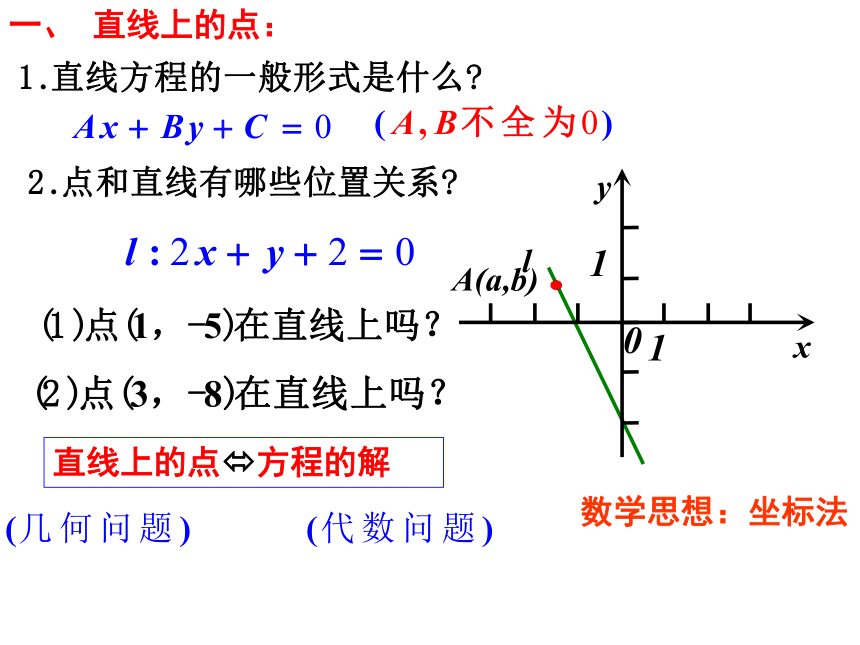
隔离分家万事休. 3.3.1两条直线的交点坐标丁海燕直线上的点?方程的解xylA(a,b)一、 直线上的点:数学思想:坐标法二.两条直线的交点坐标: (1)两直线l1:A1x+B1y+C1=0和 l2:A2x+B2y+C2=0相交,
交点为A,如何求交点坐标?x0A(a,b)l2l1y结论1:两直线交点的坐标
就是两直线方程联立方程组的解两直线交点坐标?方程组的解例1. 求l1:3x+4y-2=0与l2:2x+y+2=0的交点解:∴交点 (- 2,2)一.两条直线的交点坐标:变1.直线 y= - x+b 和 x - y=0 的交点在第一象限,
求b的取值范围.变2.设三条直线l1:3x+4y-2=0, l2:2x+y+2=0,
l3:x-(k+1)y-5=0,若这三条直线交于一点,求k的值两直线交点坐标?方程组的解代入法,加减消元法例1. 求l1:3x+4y-2=0与l2:2x+y+2=0的交点解:∴交点 (- 2,2)表示过 l1:3x+4y-2=0与l2:2x+y+2=0的交点的直线方程二.过两条直线的交点的直线系方程:注意:不含直线 l2画板过l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点
的直线方程是结论2:(A1x+B1y+C1)+λ(A2x+B2y+C2)=0注意:不含直线 l2过l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点
的直线方程是结论2:(A1x+B1y+C1)+λ(A2x+B2y+C2)=0注意:不含直线 l2二.过两条直线的交点的直线系方程:变式2,若 a+b=5, 其中a、b是实常数,
则直线ax+by-10=0必过定点________变式3.若3A+4B+5C=0,则直线Ax+By+C=0必过定点____(1)过点(0,0)变式4:分别求经过l1:3x+4y-2=0与l2:2x+y+2=0的交点
且 满足下列条件的直线的方程 (2)和l:2x-y+5=0垂直 (3)和l:2x-y+6=0平行2.你掌握了哪些数学思想方法?1.你学习了哪些知识点?课堂小结3.你最大的收获是什么?求两直线交点 两直线方程的解解的情况与
两直线位置关系 一解
?相交 无穷解
?重合 无解
?平行系数比的关系
与两直线位置关系过两直线交点的直线系方程三、两直线的位置关系 两直线的位置关系与方程组解的个数有何对应关系?两直线平行 ?方程组无解两直线相交 ?方程组有唯一解两直线重合 ?方程组有无穷多解结论2:两直线方程的系数比满足什么条件时,
两直线平行, 重合,相交,垂直?若 l1: A1x+B1y+C1=0 与 l2: A2x+B2y+C2=0,三、两直线的位置关系=> 两直线平行=> 两直线相交=> 两直线重合若 l1: A1x+B1y+C1=0 与 l2: A2x+B2y+C2=0,三、两直线的位置关系=> 两直线垂直分类讨论例4.已知两直线 l1:x+my+6=0 , l2:(m-2)x+3y+2m=0,
当m为何值时,直线l1与 l2 (1)相交,(2) 平行,(3) 垂直我国著名数学家华罗庚曾说过:数缺形时少直观,
形少数时难入微;
数形结合百般好,
隔离分家万事休. ★题:★★★题:12345★★题:课堂竞技场 1.两条直线x+my+12=0和2x+3y+m=0的交点在y轴上,
则m的值 _______
2.若直线x-y+1=0和x-ky = 0相交,且交点在第二象限, 则k的取值范围__________
4.已知不论m取何实数值,直线(m-1)x-y+2m+1=0恒过
一定点,则定点的坐标为 ___
5.当k为何值时,直线 y=kx+3过直线 2x-y+1=0与y= x+5
的交点?课堂竞技场=> 两直线平行=> 两直线相交=> 两直线重合若 l1: A1x+B1y+C1=0与l2: A2x+B2y+C2=0,三、两直线的位置关系=> 两直线垂直例3.已知两直线 l1:x+my+6=0 , l2:(m-2)x+3y+2m=0,
当m为何值时,直线l1与 l2 (1)相交,(2) 平行,(3) 垂直例1 求l1:3x+4y-2=0与l2:2x+y+2=0的交点解:∴交点 (- 2,2)画板表示过 l1:3x+4y-2=0与l2:2x+y+2=0的交点的直线方程四.过两条直线的交点的直线系方程:注意:不含直线 l2四.过两条直线的交点的直线系方程:过l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点
的直线方程是结论4:(A1x+B1y+C1)+λ(A2x+B2y+C2)=0注意:不含直线 l2λ(A1x+B1y+C1)+ (A2x+B2y+C2)=0注意:不含直线 l1λ(A1x+B1y+C1)+μ(A2x+B2y+C2)=0(2)“两直线的位置关系”与“方程组解的个数”
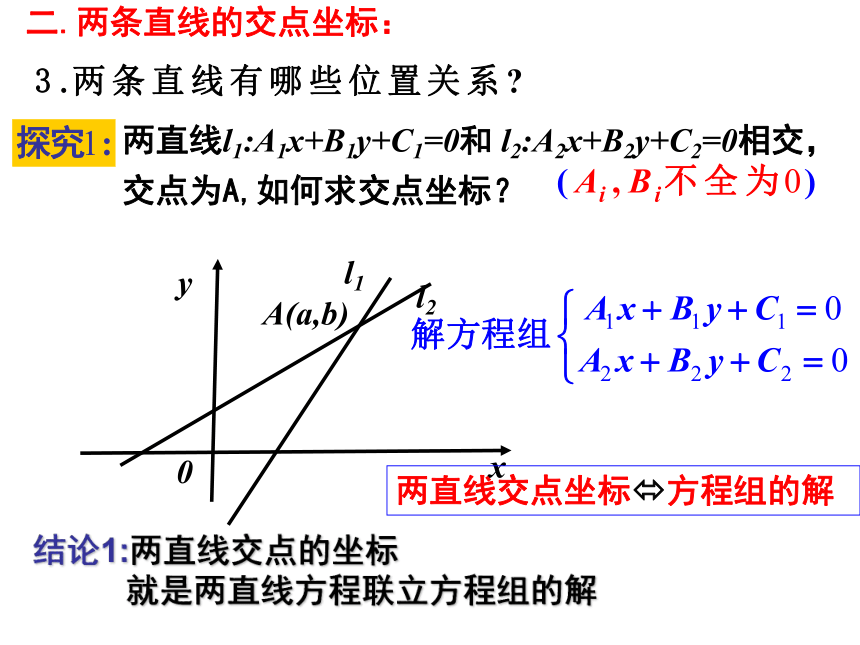
之间有何对应关系?两直线平行 ?方程组无解两直线相交 ?方程组有唯一解两直线重合 ?方程组有无穷多解结论2: (1)两直线l1:A1x+B1y+C1=0和 l2:A2x+B2y+C2=0相交,
交点为A,如何求交点坐标?二.两条直线的交点坐标:
形少数时难入微;
数形结合百般好,
隔离分家万事休. 3.3.1两条直线的交点坐标丁海燕直线上的点?方程的解xylA(a,b)一、 直线上的点:数学思想:坐标法二.两条直线的交点坐标: (1)两直线l1:A1x+B1y+C1=0和 l2:A2x+B2y+C2=0相交,
交点为A,如何求交点坐标?x0A(a,b)l2l1y结论1:两直线交点的坐标
就是两直线方程联立方程组的解两直线交点坐标?方程组的解例1. 求l1:3x+4y-2=0与l2:2x+y+2=0的交点解:∴交点 (- 2,2)一.两条直线的交点坐标:变1.直线 y= - x+b 和 x - y=0 的交点在第一象限,
求b的取值范围.变2.设三条直线l1:3x+4y-2=0, l2:2x+y+2=0,
l3:x-(k+1)y-5=0,若这三条直线交于一点,求k的值两直线交点坐标?方程组的解代入法,加减消元法例1. 求l1:3x+4y-2=0与l2:2x+y+2=0的交点解:∴交点 (- 2,2)表示过 l1:3x+4y-2=0与l2:2x+y+2=0的交点的直线方程二.过两条直线的交点的直线系方程:注意:不含直线 l2画板过l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点
的直线方程是结论2:(A1x+B1y+C1)+λ(A2x+B2y+C2)=0注意:不含直线 l2过l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点
的直线方程是结论2:(A1x+B1y+C1)+λ(A2x+B2y+C2)=0注意:不含直线 l2二.过两条直线的交点的直线系方程:变式2,若 a+b=5, 其中a、b是实常数,
则直线ax+by-10=0必过定点________变式3.若3A+4B+5C=0,则直线Ax+By+C=0必过定点____(1)过点(0,0)变式4:分别求经过l1:3x+4y-2=0与l2:2x+y+2=0的交点
且 满足下列条件的直线的方程 (2)和l:2x-y+5=0垂直 (3)和l:2x-y+6=0平行2.你掌握了哪些数学思想方法?1.你学习了哪些知识点?课堂小结3.你最大的收获是什么?求两直线交点 两直线方程的解解的情况与
两直线位置关系 一解
?相交 无穷解
?重合 无解
?平行系数比的关系
与两直线位置关系过两直线交点的直线系方程三、两直线的位置关系 两直线的位置关系与方程组解的个数有何对应关系?两直线平行 ?方程组无解两直线相交 ?方程组有唯一解两直线重合 ?方程组有无穷多解结论2:两直线方程的系数比满足什么条件时,
两直线平行, 重合,相交,垂直?若 l1: A1x+B1y+C1=0 与 l2: A2x+B2y+C2=0,三、两直线的位置关系=> 两直线平行=> 两直线相交=> 两直线重合若 l1: A1x+B1y+C1=0 与 l2: A2x+B2y+C2=0,三、两直线的位置关系=> 两直线垂直分类讨论例4.已知两直线 l1:x+my+6=0 , l2:(m-2)x+3y+2m=0,
当m为何值时,直线l1与 l2 (1)相交,(2) 平行,(3) 垂直我国著名数学家华罗庚曾说过:数缺形时少直观,
形少数时难入微;
数形结合百般好,
隔离分家万事休. ★题:★★★题:12345★★题:课堂竞技场 1.两条直线x+my+12=0和2x+3y+m=0的交点在y轴上,
则m的值 _______
2.若直线x-y+1=0和x-ky = 0相交,且交点在第二象限, 则k的取值范围__________
4.已知不论m取何实数值,直线(m-1)x-y+2m+1=0恒过
一定点,则定点的坐标为 ___
5.当k为何值时,直线 y=kx+3过直线 2x-y+1=0与y= x+5
的交点?课堂竞技场=> 两直线平行=> 两直线相交=> 两直线重合若 l1: A1x+B1y+C1=0与l2: A2x+B2y+C2=0,三、两直线的位置关系=> 两直线垂直例3.已知两直线 l1:x+my+6=0 , l2:(m-2)x+3y+2m=0,
当m为何值时,直线l1与 l2 (1)相交,(2) 平行,(3) 垂直例1 求l1:3x+4y-2=0与l2:2x+y+2=0的交点解:∴交点 (- 2,2)画板表示过 l1:3x+4y-2=0与l2:2x+y+2=0的交点的直线方程四.过两条直线的交点的直线系方程:注意:不含直线 l2四.过两条直线的交点的直线系方程:过l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点
的直线方程是结论4:(A1x+B1y+C1)+λ(A2x+B2y+C2)=0注意:不含直线 l2λ(A1x+B1y+C1)+ (A2x+B2y+C2)=0注意:不含直线 l1λ(A1x+B1y+C1)+μ(A2x+B2y+C2)=0(2)“两直线的位置关系”与“方程组解的个数”
之间有何对应关系?两直线平行 ?方程组无解两直线相交 ?方程组有唯一解两直线重合 ?方程组有无穷多解结论2: (1)两直线l1:A1x+B1y+C1=0和 l2:A2x+B2y+C2=0相交,
交点为A,如何求交点坐标?二.两条直线的交点坐标:
