15.2.2.1 完全平方公式 课件
文档属性
| 名称 | 15.2.2.1 完全平方公式 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-13 00:00:00 | ||
图片预览





文档简介
课件25张PPT。15.2.2 完全平方公式a2 ? b2平方差公式 (a+b)(a?b)=
(mn – 3)(mn +3)= ______
(– 2x-y)(2x-y)= ______m2n2 –9y2 –4x2多项式的乘法 (a+b)(c+d)acadbcbd=+++计算下列各式,你能发现什么规律?
(p+3)2 = (p+3) (p+3) = _________;
(p-1)2 = (p-1 ) (p-1) = ________;P2+6p+9P2-2p+1 合作探究(3)计算(a+b)2, (a-b)2.(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
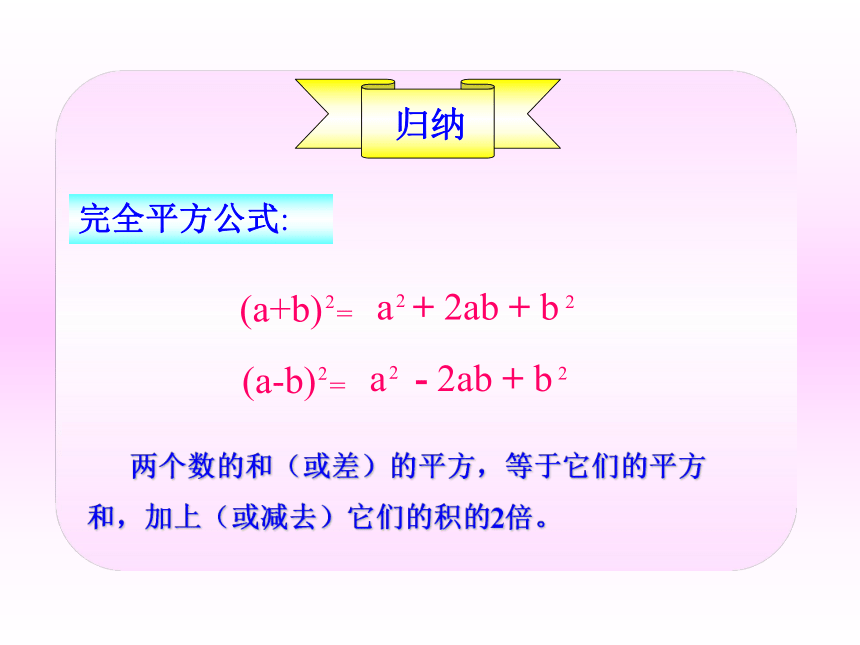
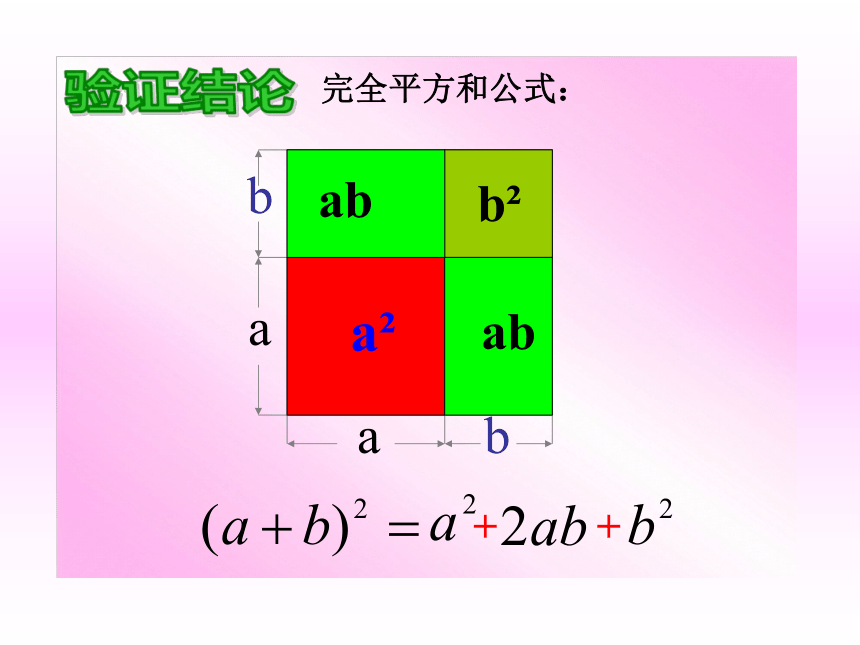
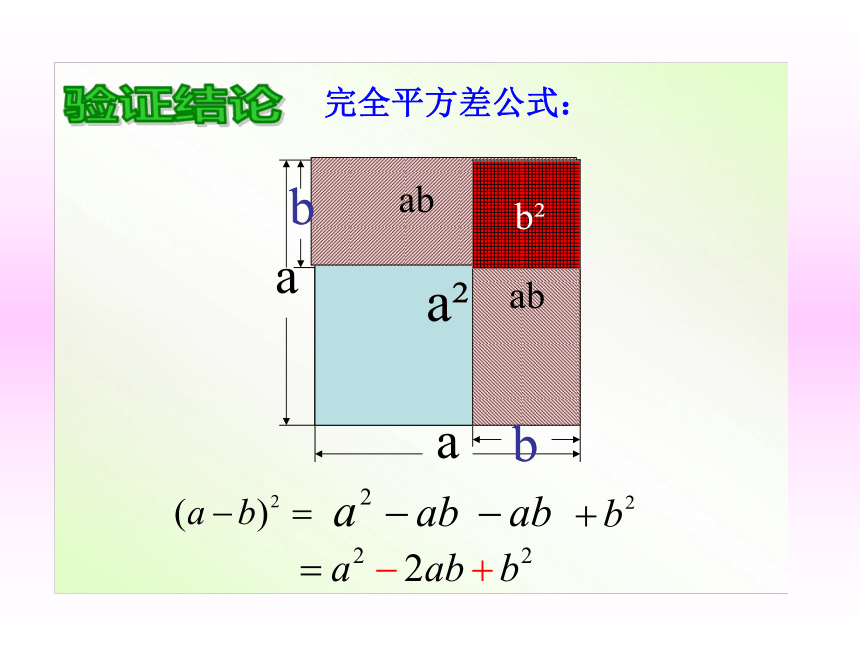
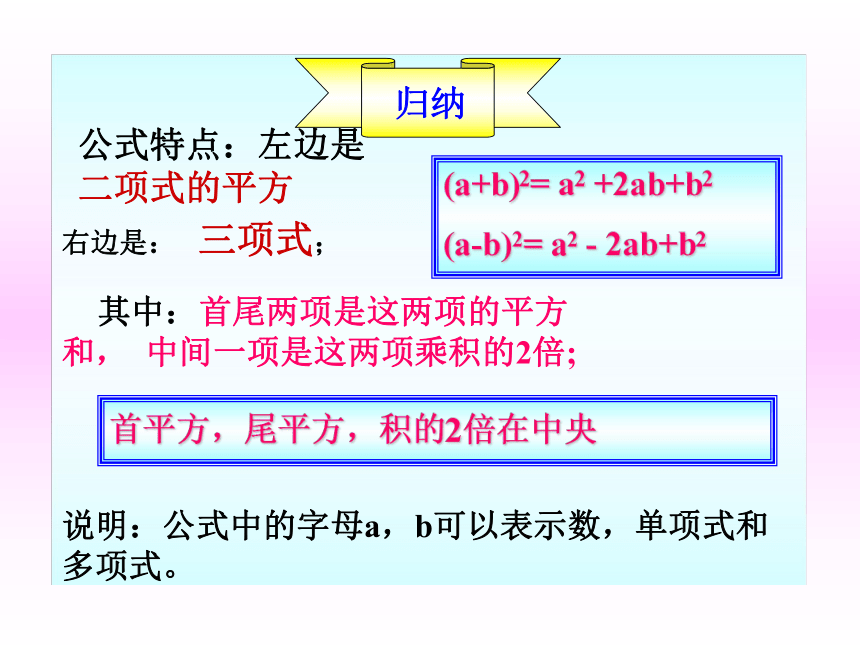
=a2-2ab+b2完全平方公式: 两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。 (a+b)2a2b2完全平方和公式:验证结论验证结论(a-b)2b2完全平方差公式:公式特点:左边是 二项式的平方说明:公式中的字母a,b可以表示数,单项式和多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2右边是: 三项式; 其中:首尾两项是这两项的平方 和, 中间一项是这两项乘积的2倍;首平方,尾平方,积的2倍在中央 ( 2x )2 ? 2 ? 2x ? 3 +32
解:(1) (2x?3)2 = 例1 利用完全平方公式计算:
(1) (2x?3)2 ; (2) (4x+5y)2 ; 4x2=?12x+9 ; (2) (4x + 5y )2 = (4x)2 + 2 · 4x · 5y + (5y)2 =16 x2 + 40 x y +25y21、下面各式的计算是否正确?如果不正确,应当怎样改正?错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (x -y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2 巩固训练填空:
1) a2+ +b2=(a - b)2
2) 4a2+ +b2=(2a+b)2
3) ( )2+4ab+b2=( +b)2
4) a2-8ab+ =( )2(-2ab)4ab2a2a16b2a-4b练习:p132-2例2 运用完全平方公式计算:
(1) 1022 ; (2) 992 .解: (1) 1022 = (100 +2) 2
= 1002 +2×100×2 + 22
= 10 000 +400 +4
= 10 404 (2) 992 = (100 -1)2
= 1002 -2×100×1+12
= 10 000 - 200 + 1
= 9 801 (1) (6a+5b)2
=36a2+60ab+25b2 (2) (4x-3y)2
=16x2-24xy+9y2 (3) (-2m+1)2
=4m2-4m+1 (4) (-2m-1)2
=4m2+4m+1 运用完全平方公式计算: (5) 1032
=(100+3)2
=1002+2×100×3+32
=10000+600+9=10609 想一想:
(a+b)2与(-a-b)2相等吗?
( a-b)2与(b-a)2也相等吗?
为什么?∵ (a+b)2=a2+2ab+b2(-a-b)2=(-a)2+2(-a)(-b)+(-b) 2=a2+2ab+b2∵ (a-b)2=a2-2ab+b2(b-a)2=b2-2ba+a2=a2-2ab+b2∴ (a+b)2= (-a-b)2∴ (a-b)2=(b-a)2 1. 下列等式是否成立? 说明理由.
(1) (?4a+1)2=(1?4a)2;
(2) (?4a?1)2=(4a+1)2;
(3) (4a?1)(1?4a)=(4a?1)(4a?1)=(4a?1)2;
(4) (4a?1)(?1?4a)=(4a?1)(4a+1). 成立 成立不成立.不成立.15.2.2 完全平方公式(2) 温故知新请同学们完成下列运算并回忆去括号法则.
(1)4+(5+2) (2)4-(5+2) (3)a+(b+c)
(4)a-(b-c)解:(1)4+(5+2)=4+5+2=11
(2)4-(5+2)=4-5-2=-3 或:4-(5+2)=4-7=-3
(3)a+(b+c)=a+b+c
(4)a-(b-c)=a-b+c去括号法则:
去括号时,如果括号前是正号,去掉括号后,括号里的每一项都不改变符合;如果括号前是负号,去掉括号后,括号里的各项都改变符合.左边没括号,右边有括号,也就是添了括号,你可不可以总结出添括号法则来呢?(1) 4+5+2=4+(5+2)(2)4-5-2=4-(5+2)
(3) a+b+c =a+(b+c)(4)a-b+c=a-(b-c)观察归纳把四个等式的左右两边反过来,即: 添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号. 1.在等号右边的括号内填上适当的项:
(1)a+b-c=a+( )
(2)a-b+c=a-( )
(3)a-b-c=a-( )
(4)a+b+c=a-( )b-cb-cb+c-b-c试一试2.判断下列运算是否正确.
(1)2a-b-c=2a-(b-c)
(2)m-3n+2a-b=m+(3n+2a-b)
(3)2x-3y+2=-(2x+3y-2)
(4)a-2b-4c+5=(a-2b)-(4c+5)×××√例 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) = [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9. 典例解析运用乘法公式计算:
(2)(2x +y +z ) (2x – y – z )=[2x +(y +z )][2x – (y +z )]
=(2x)2 –(y+z)2
=4x2 –(y2 +2yz+ z2)
=4x2 –y2 -2yz- z2 = [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.例 运用乘法公式计算:
(2) (a + b +c ) 2运用乘法公式计算:
(a + 2b – 1 ) 2 =[(a+2b)-1] 2
=(a+2b) 2 –2(a+2b)×1+12
=a2 +4ab+4b2 –2a-4b+1 巩固训练计算:(x+3)2-x2 能力挑战解法1:
原式=(x+3+x)(x+3-x)
=(2x+3)×3
=6x+9解法2:
原式= x2+6x+9-x2
=6x+9
(mn – 3)(mn +3)= ______
(– 2x-y)(2x-y)= ______m2n2 –9y2 –4x2多项式的乘法 (a+b)(c+d)acadbcbd=+++计算下列各式,你能发现什么规律?
(p+3)2 = (p+3) (p+3) = _________;
(p-1)2 = (p-1 ) (p-1) = ________;P2+6p+9P2-2p+1 合作探究(3)计算(a+b)2, (a-b)2.(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2完全平方公式: 两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。 (a+b)2a2b2完全平方和公式:验证结论验证结论(a-b)2b2完全平方差公式:公式特点:左边是 二项式的平方说明:公式中的字母a,b可以表示数,单项式和多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2右边是: 三项式; 其中:首尾两项是这两项的平方 和, 中间一项是这两项乘积的2倍;首平方,尾平方,积的2倍在中央 ( 2x )2 ? 2 ? 2x ? 3 +32
解:(1) (2x?3)2 = 例1 利用完全平方公式计算:
(1) (2x?3)2 ; (2) (4x+5y)2 ; 4x2=?12x+9 ; (2) (4x + 5y )2 = (4x)2 + 2 · 4x · 5y + (5y)2 =16 x2 + 40 x y +25y21、下面各式的计算是否正确?如果不正确,应当怎样改正?错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (x -y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2 巩固训练填空:
1) a2+ +b2=(a - b)2
2) 4a2+ +b2=(2a+b)2
3) ( )2+4ab+b2=( +b)2
4) a2-8ab+ =( )2(-2ab)4ab2a2a16b2a-4b练习:p132-2例2 运用完全平方公式计算:
(1) 1022 ; (2) 992 .解: (1) 1022 = (100 +2) 2
= 1002 +2×100×2 + 22
= 10 000 +400 +4
= 10 404 (2) 992 = (100 -1)2
= 1002 -2×100×1+12
= 10 000 - 200 + 1
= 9 801 (1) (6a+5b)2
=36a2+60ab+25b2 (2) (4x-3y)2
=16x2-24xy+9y2 (3) (-2m+1)2
=4m2-4m+1 (4) (-2m-1)2
=4m2+4m+1 运用完全平方公式计算: (5) 1032
=(100+3)2
=1002+2×100×3+32
=10000+600+9=10609 想一想:
(a+b)2与(-a-b)2相等吗?
( a-b)2与(b-a)2也相等吗?
为什么?∵ (a+b)2=a2+2ab+b2(-a-b)2=(-a)2+2(-a)(-b)+(-b) 2=a2+2ab+b2∵ (a-b)2=a2-2ab+b2(b-a)2=b2-2ba+a2=a2-2ab+b2∴ (a+b)2= (-a-b)2∴ (a-b)2=(b-a)2 1. 下列等式是否成立? 说明理由.
(1) (?4a+1)2=(1?4a)2;
(2) (?4a?1)2=(4a+1)2;
(3) (4a?1)(1?4a)=(4a?1)(4a?1)=(4a?1)2;
(4) (4a?1)(?1?4a)=(4a?1)(4a+1). 成立 成立不成立.不成立.15.2.2 完全平方公式(2) 温故知新请同学们完成下列运算并回忆去括号法则.
(1)4+(5+2) (2)4-(5+2) (3)a+(b+c)
(4)a-(b-c)解:(1)4+(5+2)=4+5+2=11
(2)4-(5+2)=4-5-2=-3 或:4-(5+2)=4-7=-3
(3)a+(b+c)=a+b+c
(4)a-(b-c)=a-b+c去括号法则:
去括号时,如果括号前是正号,去掉括号后,括号里的每一项都不改变符合;如果括号前是负号,去掉括号后,括号里的各项都改变符合.左边没括号,右边有括号,也就是添了括号,你可不可以总结出添括号法则来呢?(1) 4+5+2=4+(5+2)(2)4-5-2=4-(5+2)
(3) a+b+c =a+(b+c)(4)a-b+c=a-(b-c)观察归纳把四个等式的左右两边反过来,即: 添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号. 1.在等号右边的括号内填上适当的项:
(1)a+b-c=a+( )
(2)a-b+c=a-( )
(3)a-b-c=a-( )
(4)a+b+c=a-( )b-cb-cb+c-b-c试一试2.判断下列运算是否正确.
(1)2a-b-c=2a-(b-c)
(2)m-3n+2a-b=m+(3n+2a-b)
(3)2x-3y+2=-(2x+3y-2)
(4)a-2b-4c+5=(a-2b)-(4c+5)×××√例 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) = [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9. 典例解析运用乘法公式计算:
(2)(2x +y +z ) (2x – y – z )=[2x +(y +z )][2x – (y +z )]
=(2x)2 –(y+z)2
=4x2 –(y2 +2yz+ z2)
=4x2 –y2 -2yz- z2 = [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.例 运用乘法公式计算:
(2) (a + b +c ) 2运用乘法公式计算:
(a + 2b – 1 ) 2 =[(a+2b)-1] 2
=(a+2b) 2 –2(a+2b)×1+12
=a2 +4ab+4b2 –2a-4b+1 巩固训练计算:(x+3)2-x2 能力挑战解法1:
原式=(x+3+x)(x+3-x)
=(2x+3)×3
=6x+9解法2:
原式= x2+6x+9-x2
=6x+9
