沪科版数学八年级下册 18.1勾股定理-课件(共37张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1勾股定理-课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 11:30:51 | ||
图片预览








文档简介
(共37张PPT)
勾股定理
——数形结合之美
相信自己是最棒的
C
B
A
学习目标
1、掌握《勾股定理》的内容(重点)
2、经历探索和验证勾股定理的过程,发展对图形性质或数量关系猜想及检验能力,感受解决同一个问题方法的多样性。 (难点)
3、能应用勾股定理进行简单的计算,感受勾股定理的应用价值。
y=0
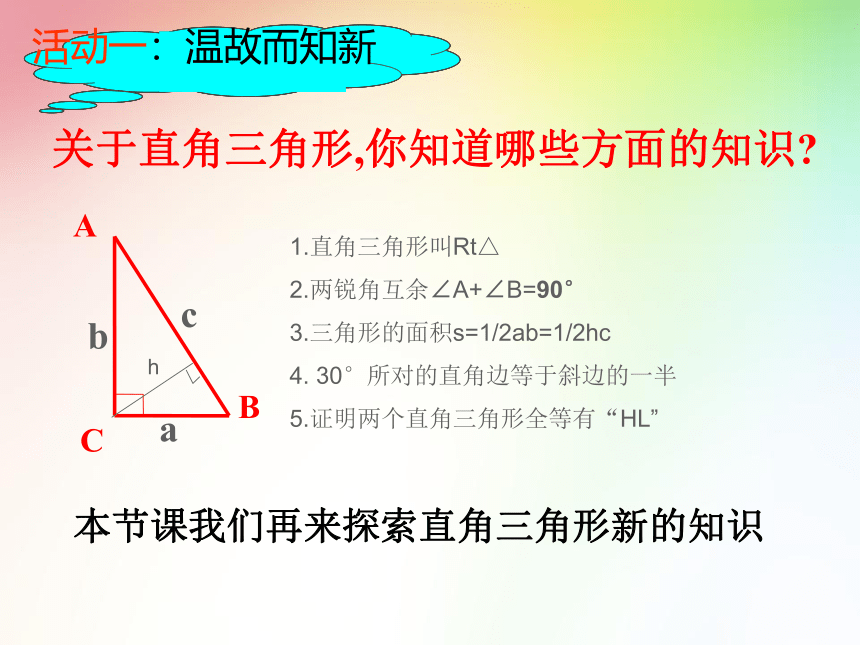
关于直角三角形,你知道哪些方面的知识
A
B
C
a
c
b
1.直角三角形叫Rt△
2.两锐角互余∠A+∠B=90°
3.三角形的面积s=1/2ab=1/2hc
4. 30°所对的直角边等于斜边的一半
5.证明两个直角三角形全等有“HL”
活动一:温故而知新
h
本节课我们再来探索直角三角形新的知识
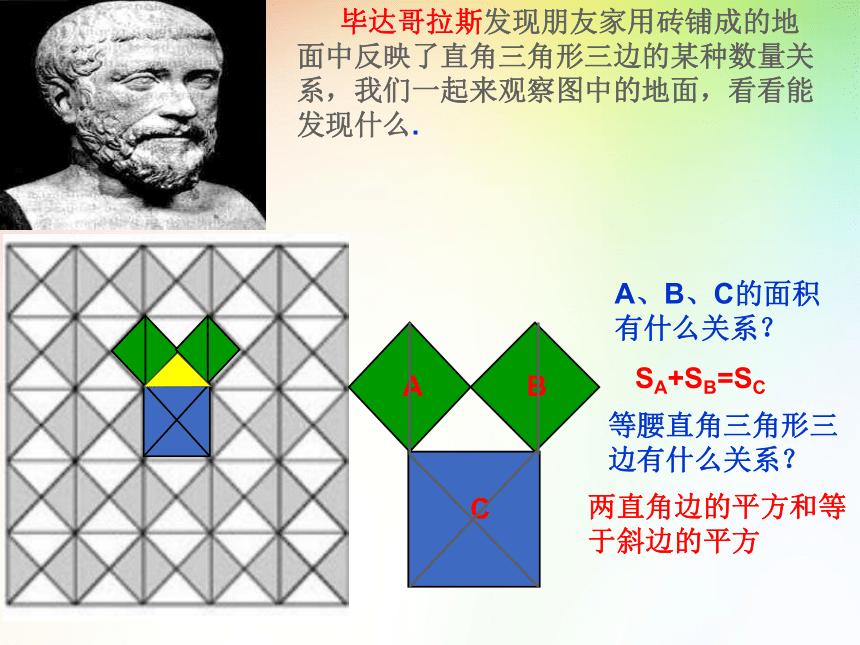
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,你想知道大哲学家发现了什么吗?
活动二 听故事
情景导入:
毕达哥拉斯发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么.
A、B、C的面积
有什么关系?
等腰直角三角形三
边有什么关系?
SA+SB=SC
两直角边的平方和等
于斜边的平方
A
B
C
毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.勾股定理流传最广的证明载于欧几里德(Euclid,是公元前三百年左右的人)的《几何原本》中,欧几里德在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
1955年希腊发行了一张邮票,图案是由三个棋盘排列而成.这张邮票也是为了纪念勾股定理这个伟大的发现.
1955年希腊发行的印有勾股定理图案的
邮票
百 牛 定 理
勾股史话
商高定理:
商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。
商高定理就是勾股定理哦!
A
B
C
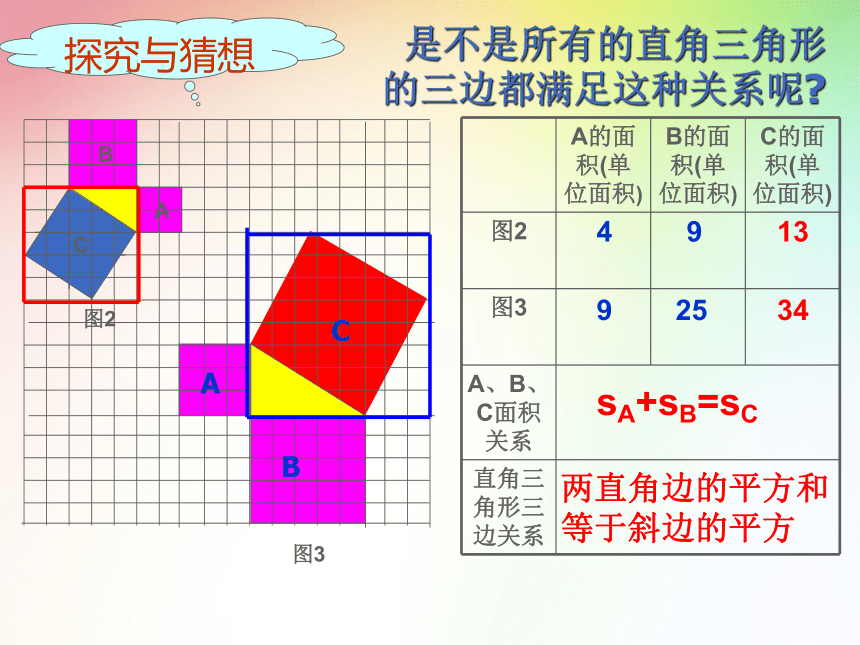
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图2
图3
A、B、C面积关系 直角三角形三边关系 图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
探究与猜想
是不是所有的直角三角形的三边都满足这种关系呢
A
B
C
想一想:我们怎样用面积计算的方法来证
明勾股定理呢?
已知:如图,在Rt△ABC中,,∠C=90°,
AB=c,BC=a,AC=b,
求证:a2+b2=c2.
c
c
c
c
a
b
a
b
a
b
a
b
a
b
c
A
C
B
A1
B1
C1
D1
E
F
G
H
证法一:P53
证明:由拼图可知:大正方形的边长为(a+b),
小正方形的边长为c,
∵ 大正方形EFGH的面积减去4个△ABC的面
积等于中间的小正方形A1B1C1D1的面积.
化简,得:
a2+b2=c2
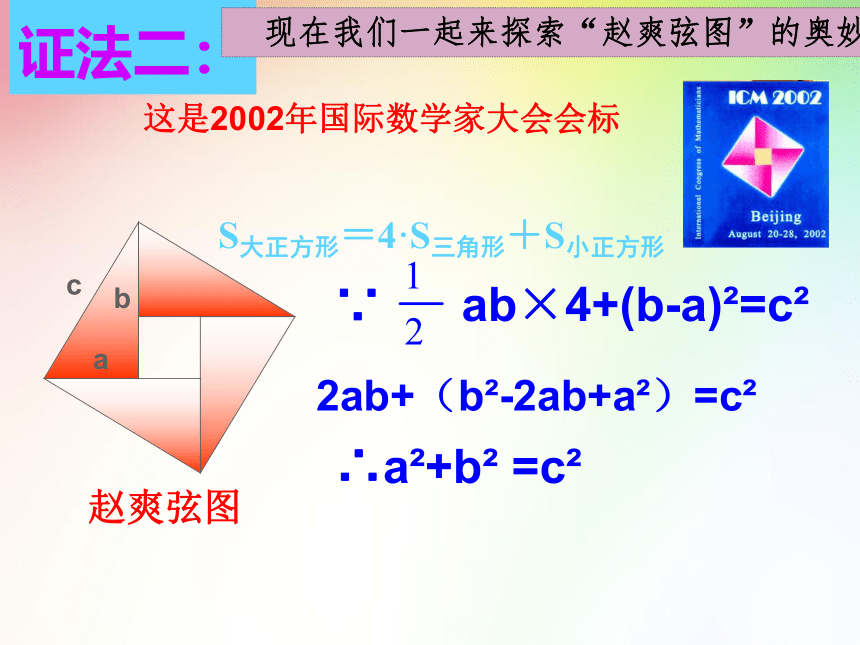
这是2002年国际数学家大会会标
赵爽弦图
∵ ab×4+(b-a) =c
∴a +b =c
a
b
c
2ab+(b -2ab+a )=c
证法二:
S大正方形=4·S三角形+S小正方形
现在我们一起来探索“赵爽弦图”的奥妙吧!
美国总统证法
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,由于好奇心驱使,加菲尔德循声向两个小孩走去。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他们在干什么?
证法三:
美国总统证法
那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。
a
b
c
b
a
c
A
B
C
D
E
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
能只用这两个直角三角形说明a2+b2=c2吗?
拼一拼 试一试
勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
现在在网络上看到较多的是16种,包括前面的6种,还有:
欧几里得证明、 利用相似三角形性质证明、
杨作玫证明、 李锐证明、
利用切割线定理证明、 利用多列米定理证明、
作直角三角形的内切圆证明、利用反证法证明、
辛卜松证明、 陈杰证明。
走进数学史
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
结论:
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现
通过这种方法,可以把一个正方形的面积分成若干
个小正方形的面积的和,不断地分下去,就可以得到一
棵美丽的勾股树.
归纳探究
课堂练习:.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
练一练
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
在用勾股定理时,需要知道直角三角形
中的两条边长,才能求出第三边长.
c
b
a
公式变形
a2 + b2 = c2
c2=a2 + b2
a2=a2 = c2 - b2
c2-b2
b2b2 = c2 - a2
=c2-a2
勾股小常识:勾股数
1.基本勾股数如:大家一定要熟记
2.如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
如:
6、8、10 ; 9、12、15;
10、24、26 ; 15、36、39……
1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
试一试:
3
4
2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
A
试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
5 或
4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
例3 现在一楼房发生火灾,消防队员决定用消防车上的云梯救人。已知最多只能伸长10m,消防车高3m.救人是云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
例题讲解》:P54
D
B
E
图18-3
C
A
O
分析:如图18-3,设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O。则OB=9-3=6(m),OD=12-3=9(m).
根据勾股定理,得
解方程,得
设AC=X,则OC=8-x,于是根据勾股定理,得
请根据上述分析写出解题过程
在我国古代数学著作《九章算术》中记载了一道有趣的问题:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?
A
C
B
讲授新课
问题探究: (古代问题)
这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少尺?
D
A
B
C
解:设水池的深度AC为X尺,
则芦苇高AD为 (X+1)尺.
根据题意得:
BC2+AC2=AB2
∴52+X2 =(X+1)2
25+X2=X2+2X+1
X=12
∴X+1=12+1=13(尺)
答:水池的深度为12尺,芦苇的长度为13尺.
问题探究:
数学探索:观察下列表格:
……
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
84
85
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。
(1)
(2)
数学奇闻
有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
20尺
3×7=21(尺)
聪明的葛藤
收获无处不在
我知道了… …
我感受了… …
我探索了… …
勾
股
定
理
数
形
c2=a2+b2
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程.
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想.
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育.
课堂小结:
2、查阅有关勾股定理的历史资料.
作业
1、课堂作业:
课本57页,第1、2、3、题;
再 见
勾股定理
——数形结合之美
相信自己是最棒的
C
B
A
学习目标
1、掌握《勾股定理》的内容(重点)
2、经历探索和验证勾股定理的过程,发展对图形性质或数量关系猜想及检验能力,感受解决同一个问题方法的多样性。 (难点)
3、能应用勾股定理进行简单的计算,感受勾股定理的应用价值。
y=0
关于直角三角形,你知道哪些方面的知识
A
B
C
a
c
b
1.直角三角形叫Rt△
2.两锐角互余∠A+∠B=90°
3.三角形的面积s=1/2ab=1/2hc
4. 30°所对的直角边等于斜边的一半
5.证明两个直角三角形全等有“HL”
活动一:温故而知新
h
本节课我们再来探索直角三角形新的知识
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,你想知道大哲学家发现了什么吗?
活动二 听故事
情景导入:
毕达哥拉斯发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么.
A、B、C的面积
有什么关系?
等腰直角三角形三
边有什么关系?
SA+SB=SC
两直角边的平方和等
于斜边的平方
A
B
C
毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.勾股定理流传最广的证明载于欧几里德(Euclid,是公元前三百年左右的人)的《几何原本》中,欧几里德在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
1955年希腊发行了一张邮票,图案是由三个棋盘排列而成.这张邮票也是为了纪念勾股定理这个伟大的发现.
1955年希腊发行的印有勾股定理图案的
邮票
百 牛 定 理
勾股史话
商高定理:
商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。
商高定理就是勾股定理哦!
A
B
C
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图2
图3
A、B、C面积关系 直角三角形三边关系 图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
探究与猜想
是不是所有的直角三角形的三边都满足这种关系呢
A
B
C
想一想:我们怎样用面积计算的方法来证
明勾股定理呢?
已知:如图,在Rt△ABC中,,∠C=90°,
AB=c,BC=a,AC=b,
求证:a2+b2=c2.
c
c
c
c
a
b
a
b
a
b
a
b
a
b
c
A
C
B
A1
B1
C1
D1
E
F
G
H
证法一:P53
证明:由拼图可知:大正方形的边长为(a+b),
小正方形的边长为c,
∵ 大正方形EFGH的面积减去4个△ABC的面
积等于中间的小正方形A1B1C1D1的面积.
化简,得:
a2+b2=c2
这是2002年国际数学家大会会标
赵爽弦图
∵ ab×4+(b-a) =c
∴a +b =c
a
b
c
2ab+(b -2ab+a )=c
证法二:
S大正方形=4·S三角形+S小正方形
现在我们一起来探索“赵爽弦图”的奥妙吧!
美国总统证法
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国共和党议员加菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,由于好奇心驱使,加菲尔德循声向两个小孩走去。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他们在干什么?
证法三:
美国总统证法
那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。
a
b
c
b
a
c
A
B
C
D
E
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
能只用这两个直角三角形说明a2+b2=c2吗?
拼一拼 试一试
勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
现在在网络上看到较多的是16种,包括前面的6种,还有:
欧几里得证明、 利用相似三角形性质证明、
杨作玫证明、 李锐证明、
利用切割线定理证明、 利用多列米定理证明、
作直角三角形的内切圆证明、利用反证法证明、
辛卜松证明、 陈杰证明。
走进数学史
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
结论:
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现
通过这种方法,可以把一个正方形的面积分成若干
个小正方形的面积的和,不断地分下去,就可以得到一
棵美丽的勾股树.
归纳探究
课堂练习:.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
练一练
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
在用勾股定理时,需要知道直角三角形
中的两条边长,才能求出第三边长.
c
b
a
公式变形
a2 + b2 = c2
c2=a2 + b2
a2=a2 = c2 - b2
c2-b2
b2b2 = c2 - a2
=c2-a2
勾股小常识:勾股数
1.基本勾股数如:大家一定要熟记
2.如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
如:
6、8、10 ; 9、12、15;
10、24、26 ; 15、36、39……
1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
试一试:
3
4
2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
A
试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
5 或
4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
例3 现在一楼房发生火灾,消防队员决定用消防车上的云梯救人。已知最多只能伸长10m,消防车高3m.救人是云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
例题讲解》:P54
D
B
E
图18-3
C
A
O
分析:如图18-3,设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O。则OB=9-3=6(m),OD=12-3=9(m).
根据勾股定理,得
解方程,得
设AC=X,则OC=8-x,于是根据勾股定理,得
请根据上述分析写出解题过程
在我国古代数学著作《九章算术》中记载了一道有趣的问题:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?
A
C
B
讲授新课
问题探究: (古代问题)
这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少尺?
D
A
B
C
解:设水池的深度AC为X尺,
则芦苇高AD为 (X+1)尺.
根据题意得:
BC2+AC2=AB2
∴52+X2 =(X+1)2
25+X2=X2+2X+1
X=12
∴X+1=12+1=13(尺)
答:水池的深度为12尺,芦苇的长度为13尺.
问题探究:
数学探索:观察下列表格:
……
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
84
85
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。
(1)
(2)
数学奇闻
有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
20尺
3×7=21(尺)
聪明的葛藤
收获无处不在
我知道了… …
我感受了… …
我探索了… …
勾
股
定
理
数
形
c2=a2+b2
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程.
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想.
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育.
课堂小结:
2、查阅有关勾股定理的历史资料.
作业
1、课堂作业:
课本57页,第1、2、3、题;
再 见
