高中人教A版数学3.1.2用二分法求方程的近似解ppt课件
文档属性
| 名称 | 高中人教A版数学3.1.2用二分法求方程的近似解ppt课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 34.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-13 22:24:13 | ||
图片预览






文档简介
课件56张PPT。3.1.2用二分法求
方程的近似解复 习 引 入 函数f(x)=lnx+2x-6=0在区间(2,3)
内有零点如何找出这个零点?游戏:请你模仿李咏主持一下幸运52,
请同学们猜一下下面这部手机的价格.游戏:请你模仿李咏主持一下幸运52,
请同学们猜一下下面这部手机的价格.思考:如何做才能以最快的速度猜出它的价格?游戏:请你模仿李咏主持一下幸运52,
请同学们猜一下下面这部手机的价格. 利用我们猜价格的方法,你能否求
解方程lnx+2x-6=0?如果能求解的话,
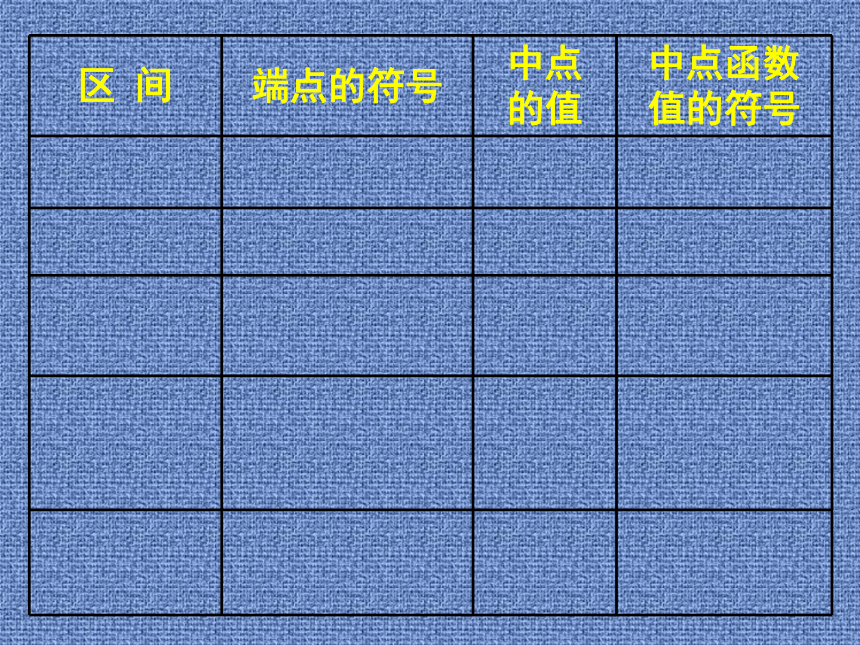
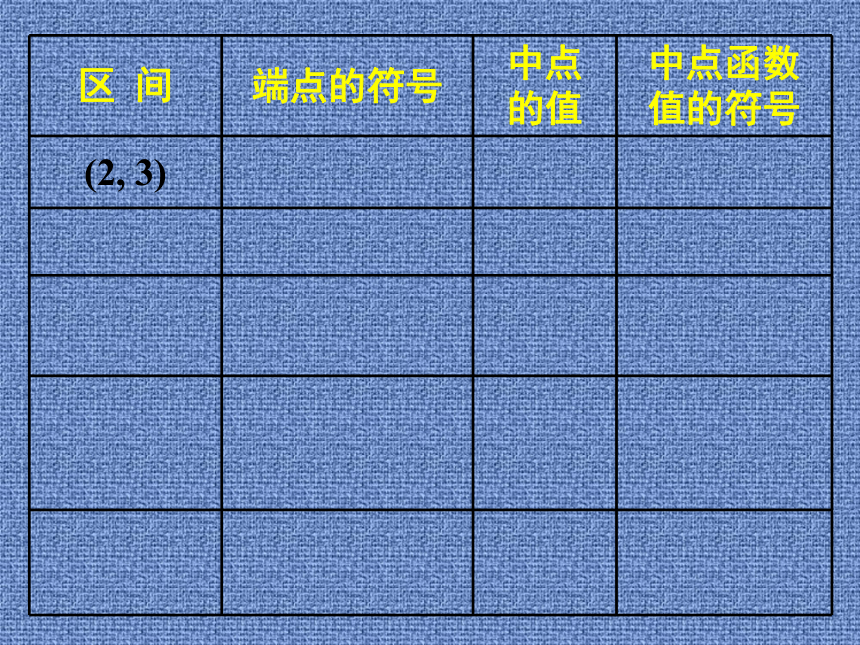
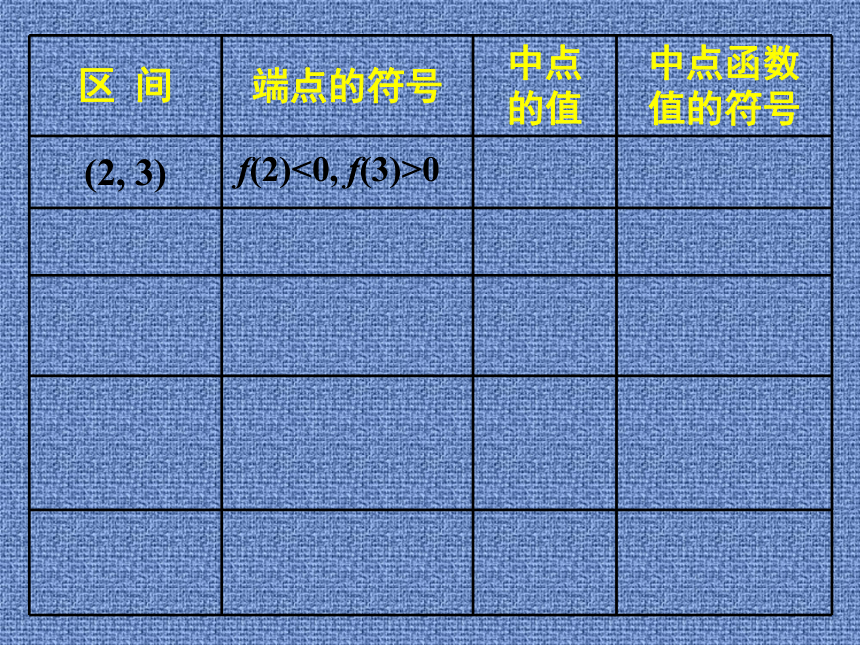
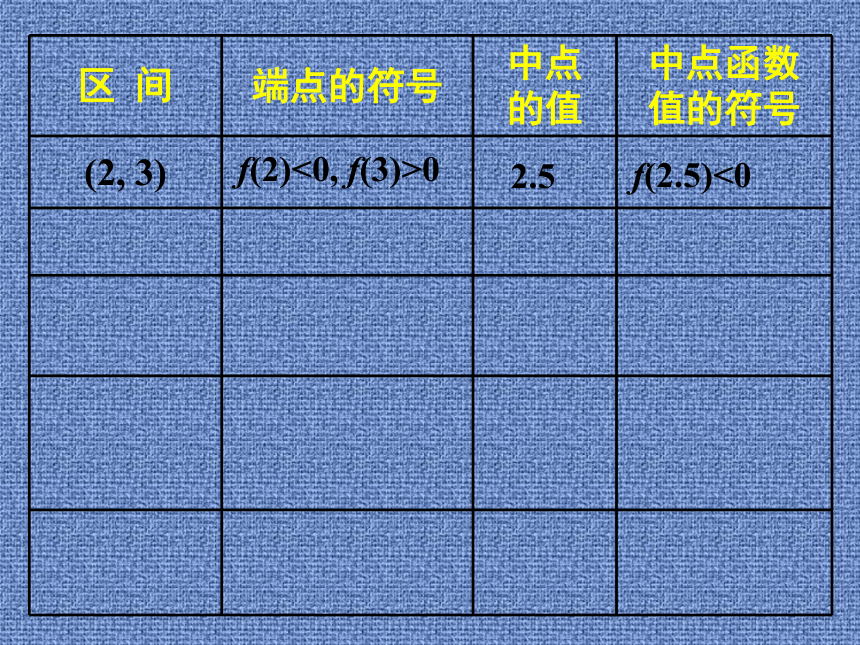
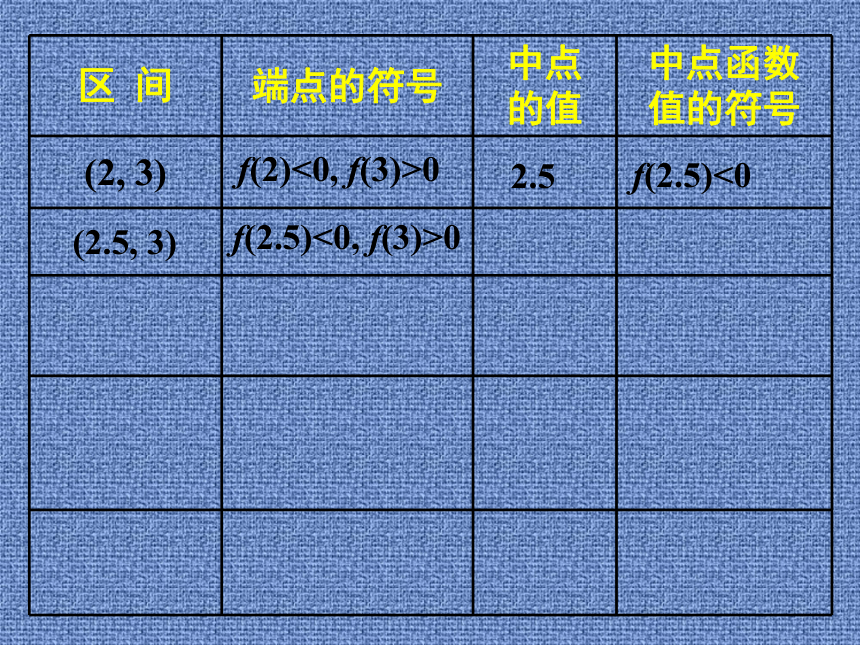
怎么去解?思考:如何做才能以最快的速度猜出它的价格?探究f(2)<0, f(3)>0f(2)<0, f(3)>02.5f(2)<0, f(3)>02.5f(2.5)<0f(2)<0, f(3)>02.5f(2.5)<0(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>0(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0(2.5, 3)f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 2.75)f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 2.5625)f(2.5)<0,
f( 2.5625)>02.53125f(2.53125)<0播放动画讲 授 新 课二分法的定义讲 授 新 课 对于在区间[a,b]上连续不断且
f (a)·f (b)<0的函数y=f (x),通过不
断地把函数f(x)的零点所在的区间一
分为二,使区间的两个端点逐步逼
近零点,进而得到零点近似值的方
法叫做二分法.二分法的定义用二分法求函数f(x)零点近似值的步骤:用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;(2) 若f(a)·f(c)<0, 则令b=c(此时零点x0∈(a,c));用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;(2) 若f(a)·f(c)<0, 则令b=c(此时零点x0∈(a,c));(3) 若f(c)·f(b)<0, 则令a=c(此时零点x0∈(c,b)).用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;(2) 若f(a)·f(c)<0, 则令b=c(此时零点x0∈(a,c));(3) 若f(c)·f(b)<0, 则令a=c(此时零点x0∈(c,b)).4.判断是否达到精确度?: 即若|a-b|<?,则得
到零点近似值a(或b), 否则重复2~4.例1 用二分法求函数f (x)=x3-3的一个
正实数零点(精确到0.1).列表列表列表列表列表列表列表列表列表列表列表列表列表播放动画例2 借助计算器或计算机用二分法求方
程2x+3x=7的近似解(精确度0.1).例2 借助计算器或计算机用二分法求方
程2x+3x=7的近似解(精确度0.1).列表因为f(1)·f(2)<0,所以 f(x)=2x+3x-7在
(1, 2)内有零点x0,取(1, 2)的中点x1=1.5,
f(1.5)=0.33,因为f(1)·f(1.5)<0
所以x0∈(1, 1.5).取(1, 1.5)的中点x2=1.25,f(1.25)=-0.87,
因为f(1.25)·f(1.5)<0,所以x0∈(1.25, 1.5).因为f(1)·f(2)<0,所以 f(x)=2x+3x-7在
(1, 2)内有零点x0,取(1, 2)的中点x1=1.5,
f(1.5)=0.33,因为f(1)·f(1.5)<0
所以x0∈(1, 1.5).同理可得, x0∈(1.375, 1.5),
x0∈(1.375, 1.4375),
由于 |1.375-1.4375|=0.0625<0.1,
所以,原方程的近似解可取为1.4375.取(1, 1.5)的中点x2=1.25,f(1.25)=-0.87,
因为f(1.25)·f(1.5)<0,所以x0∈(1.25, 1.5).因为f(1)·f(2)<0,所以 f(x)=2x+3x-7在
(1, 2)内有零点x0,取(1, 2)的中点x1=1.5,
f(1.5)=0.33,因为f(1)·f(1.5)<0
所以x0∈(1, 1.5).例2 借助计算器或计算机用二分法求方
程2x+3x=7的近似解(精确度0.1).播放动画课 堂 小 结1. 二分法的定义;
课 堂 小 结1. 二分法的定义;
2. 用二分法求函数零点近似值的步骤.课 后 作 业2. 《习案》作业三十.1. 阅读教材P.89~ P.91.
方程的近似解复 习 引 入 函数f(x)=lnx+2x-6=0在区间(2,3)
内有零点如何找出这个零点?游戏:请你模仿李咏主持一下幸运52,
请同学们猜一下下面这部手机的价格.游戏:请你模仿李咏主持一下幸运52,
请同学们猜一下下面这部手机的价格.思考:如何做才能以最快的速度猜出它的价格?游戏:请你模仿李咏主持一下幸运52,
请同学们猜一下下面这部手机的价格. 利用我们猜价格的方法,你能否求
解方程lnx+2x-6=0?如果能求解的话,
怎么去解?思考:如何做才能以最快的速度猜出它的价格?探究f(2)<0, f(3)>0f(2)<0, f(3)>02.5f(2)<0, f(3)>02.5f(2.5)<0f(2)<0, f(3)>02.5f(2.5)<0(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>0(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 3)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 3)(2.5, 2.75)f(2)<0, f(3)>02.5f(2.5)<0(2.5, 3)f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 2.75)f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 2.5625)f(2.5)<0,
f( 2.5625)>02.53125f(2.53125)<0播放动画讲 授 新 课二分法的定义讲 授 新 课 对于在区间[a,b]上连续不断且
f (a)·f (b)<0的函数y=f (x),通过不
断地把函数f(x)的零点所在的区间一
分为二,使区间的两个端点逐步逼
近零点,进而得到零点近似值的方
法叫做二分法.二分法的定义用二分法求函数f(x)零点近似值的步骤:用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;(2) 若f(a)·f(c)<0, 则令b=c(此时零点x0∈(a,c));用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;(2) 若f(a)·f(c)<0, 则令b=c(此时零点x0∈(a,c));(3) 若f(c)·f(b)<0, 则令a=c(此时零点x0∈(c,b)).用二分法求函数f(x)零点近似值的步骤:1.确定区间[a, b], 验证f(a)·f(b)<0, 给定精确度?;2.求区间(a, b)的中点c;3.计算f(c);(1) 若f(c)=0, 则c就是函数的零点;(2) 若f(a)·f(c)<0, 则令b=c(此时零点x0∈(a,c));(3) 若f(c)·f(b)<0, 则令a=c(此时零点x0∈(c,b)).4.判断是否达到精确度?: 即若|a-b|<?,则得
到零点近似值a(或b), 否则重复2~4.例1 用二分法求函数f (x)=x3-3的一个
正实数零点(精确到0.1).列表列表列表列表列表列表列表列表列表列表列表列表列表播放动画例2 借助计算器或计算机用二分法求方
程2x+3x=7的近似解(精确度0.1).例2 借助计算器或计算机用二分法求方
程2x+3x=7的近似解(精确度0.1).列表因为f(1)·f(2)<0,所以 f(x)=2x+3x-7在
(1, 2)内有零点x0,取(1, 2)的中点x1=1.5,
f(1.5)=0.33,因为f(1)·f(1.5)<0
所以x0∈(1, 1.5).取(1, 1.5)的中点x2=1.25,f(1.25)=-0.87,
因为f(1.25)·f(1.5)<0,所以x0∈(1.25, 1.5).因为f(1)·f(2)<0,所以 f(x)=2x+3x-7在
(1, 2)内有零点x0,取(1, 2)的中点x1=1.5,
f(1.5)=0.33,因为f(1)·f(1.5)<0
所以x0∈(1, 1.5).同理可得, x0∈(1.375, 1.5),
x0∈(1.375, 1.4375),
由于 |1.375-1.4375|=0.0625<0.1,
所以,原方程的近似解可取为1.4375.取(1, 1.5)的中点x2=1.25,f(1.25)=-0.87,
因为f(1.25)·f(1.5)<0,所以x0∈(1.25, 1.5).因为f(1)·f(2)<0,所以 f(x)=2x+3x-7在
(1, 2)内有零点x0,取(1, 2)的中点x1=1.5,
f(1.5)=0.33,因为f(1)·f(1.5)<0
所以x0∈(1, 1.5).例2 借助计算器或计算机用二分法求方
程2x+3x=7的近似解(精确度0.1).播放动画课 堂 小 结1. 二分法的定义;
课 堂 小 结1. 二分法的定义;
2. 用二分法求函数零点近似值的步骤.课 后 作 业2. 《习案》作业三十.1. 阅读教材P.89~ P.91.
