高中人教A版数学3.2.1几类不同增长的函数模型(一)ppt课件
文档属性
| 名称 | 高中人教A版数学3.2.1几类不同增长的函数模型(一)ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 47.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-13 22:26:01 | ||
图片预览








文档简介
课件40张PPT。3.2.1几类不同增长
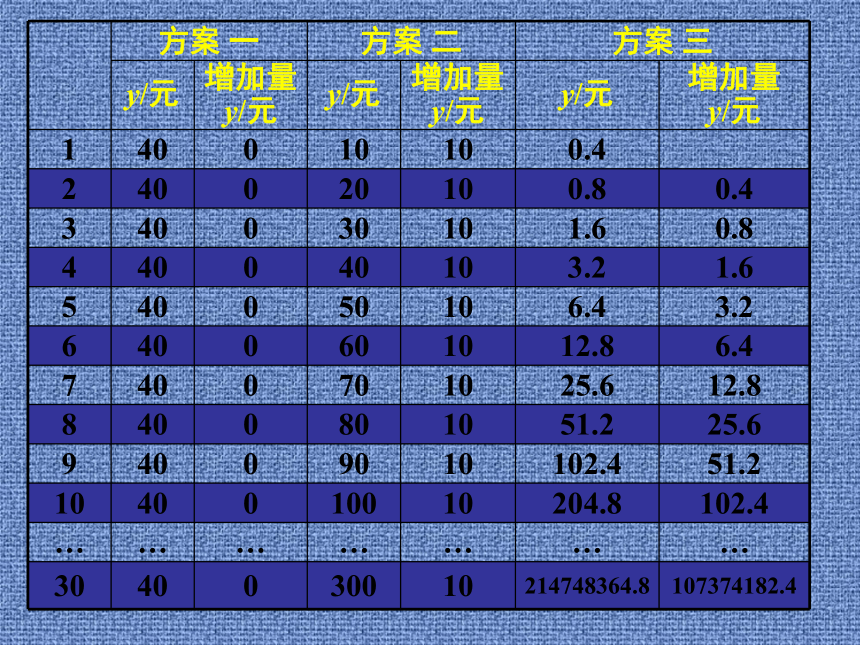
的函数模型(一)复 习 引 入讲 授 新 课例1 假设你有一笔资金用于投资,现在有
三种投资方案供你选择,这三种方案的回
报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前
一天多回报10元;
方案三:第一天回报0.4元,以后每天的回
报比前一天翻一番.
请问,你会选择哪种投资方案?解:设第x天所得回报是y元,
解:设第x天所得回报是y元,
则方案一可以用函数y=40(x∈N*)进行描述;解:设第x天所得回报是y元,
则方案一可以用函数y=40(x∈N*)进行描述;
方案二可以用函数y=10x (x∈N*)进行
描述;解:设第x天所得回报是y元,
则方案一可以用函数y=40(x∈N*)进行描述;
方案二可以用函数y=10x (x∈N*)进行
描述;
方案三可以用函数y=0.4×2x-1(x∈N*)
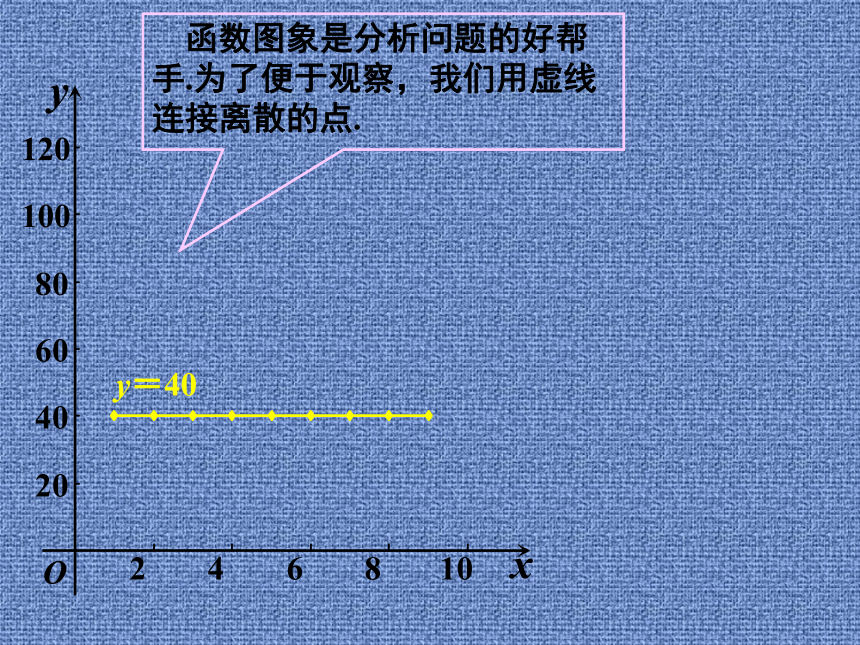
进行描述.20406080100120246810Oyx 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40 函数图象是分析问题的好帮
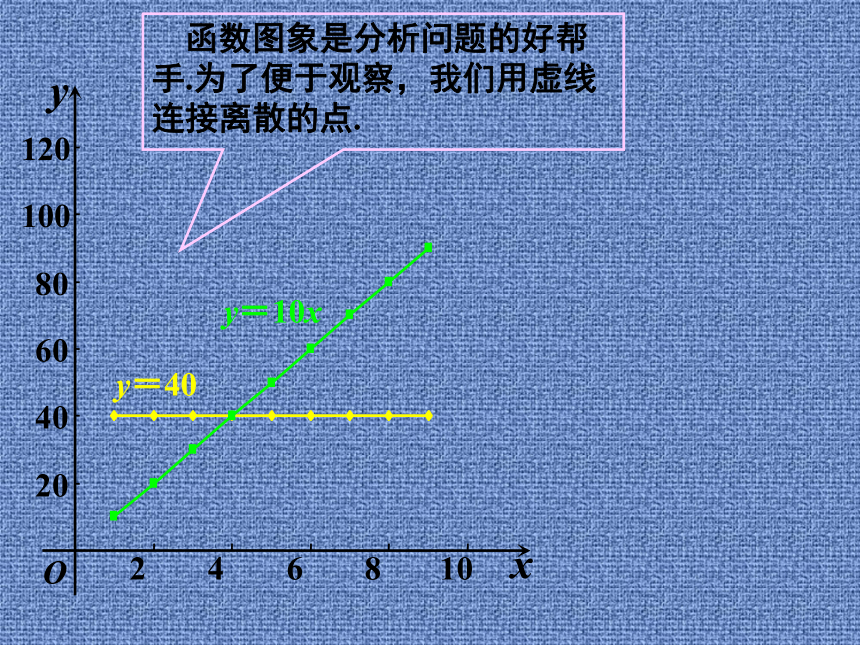
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40y=10x 函数图象是分析问题的好帮
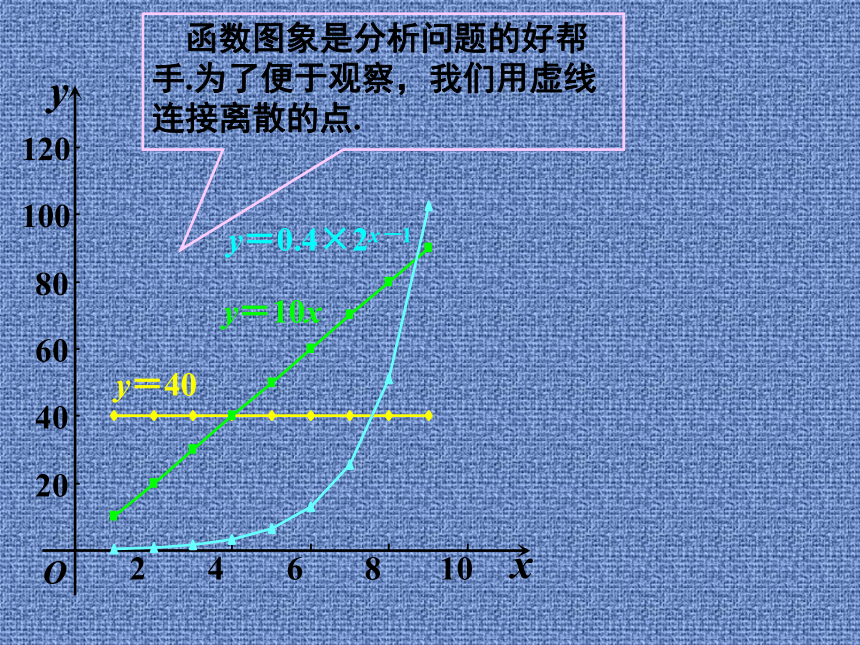
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40y=10xy=0.4×2x-1 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40y=10xy=0.4×2x-1 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点. 我们看到,底为
2的指数函数模型
比线性函数模型增
长速度要快得多.从中你对“指数爆
炸”的含义有什么
新的理解?
20406080100120246810Oyxy=40y=10x 根据以上的分
析,是否应作这样
的选择: 投资5天以
下选方案一,投资
5~8天选方案二,
投资8天以上选方
案三?y=0.4×2x-1例2 某公司为了实现1000万元利润的目标,
准备制定一个激励销售部门的奖励方案:
在销售利润达到10万元时,按销售利润进
行奖励,且奖金y(单位:万元)随销售利润
x(单位:万元)的增加而增加,但奖金总数
不超过5万元,同时奖金总数不超过利润
的25%,现有三个奖励模型:
y=0.25x, y=log7x+1, y=1.002x,
其中哪个模型能符合公司的要求?分析:某个奖励模型符合公司要求,就是
依据这个模型进行奖励时,奖金总数不超
过5万元,同时奖金不超过利润的25%,
由于公司总的利润目标为1000万元,所以
部门销售利润一般不会超过公司总的利润.
于是,只需在区间[10,1000]上,检验三个
模型是否符合公司要求即可.分析:某个奖励模型符合公司要求,就是
依据这个模型进行奖励时,奖金总数不超
过5万元,同时奖金不超过利润的25%,
由于公司总的利润目标为1000万元,所以
部门销售利润一般不会超过公司总的利润.
于是,只需在区间[10,1000]上,检验三个
模型是否符合公司要求即可. 不妨先作出函数图象,通过观察函数
的图象,得到初步的结论再通过具体计算,
确认结果.812345672004006008001000Oyx图象812345672004006008001000Oyxy=5图象812345672004006008001000y=0.25xOyxy=5图象812345672004006008001000y=0.25xy=log7x+1Oyxy=5图象812345672004006008001000y=0.25xy=log7x+1y=1.002xOyxy=5图象解: 借助计算机作出函数y=0.25x, y=log7x+1,
y=1.002x的图象.观察图象发现,在区间[10,1000]
上,模型y=0.25x,y=1.002x的图象都有一部分在
直线y=5的上方,只有模型y=log7x+1的图象始终
在y=5的下方,这
说明只有按模型
y=log7x+1进行
奖励时才符合公
司的要求,下面
通过计算确认上
述判断. 首选计算哪个模型的奖金总数不超过5万.解: 首选计算哪个模型的奖金总数不超过5万. 对于模型y=0.25x,它在区间[10, 1000]上递增,
而且当x=20时,y=5,因此,当x>20时,y>5,
所以该模型不符合要求;解: 首选计算哪个模型的奖金总数不超过5万. 对于模型y=0.25x,它在区间[10, 1000]上递增,
而且当x=20时,y=5,因此,当x>20时,y>5,
所以该模型不符合要求; 对于模型y=1.002x,由函数图象,并利用计算
器,可知在区间(805, 806) 内有一个点x0满足
1.002x=5,由于它在区间[10,1000]上递增,因此当
x>x0时,y>5,所以该模型也不符合要求;解: 首选计算哪个模型的奖金总数不超过5万. 对于模型y=0.25x,它在区间[10, 1000]上递增,
而且当x=20时,y=5,因此,当x>20时,y>5,
所以该模型不符合要求; 对于模型y=1.002x,由函数图象,并利用计算
器,可知在区间(805, 806) 内有一个点x0满足
1.002x=5,由于它在区间[10,1000]上递增,因此当
x>x0时,y>5,所以该模型也不符合要求; 对于模型y=log7x+1,它在区间[10,1000] 上递
增,而且当x=1000时,y=log71000+1≈4.55<5,
所以它符合奖金总数不超过5万元的要求. 解: 再计算按模型 y=log7x+1奖励时,奖金是否
不超过利润的25%,即当x∈[10,1000]时,是否有 成立.解: 令f(x)=log7x+1-0.25,x∈[10,1000].利用计
算机作出函数f(x)的图象,由图象可知它是递减的,
因此f(x)<f(10)≈-0.3167<0,即log7x+1<0.25x.
所以当x∈[10,1000]时, 再计算按模型 y=log7x+1奖励时,奖金是否
不超过利润的25%,即当x∈[10,1000]时,是否有 成立.解:模型y=log7x+1奖励时, 奖金不会超过利润的25%.. 说明按 令f(x)=log7x+1-0.25,x∈[10,1000].利用计
算机作出函数f(x)的图象,由图象可知它是递减的,
因此f(x)<f(10)≈-0.3167<0,即log7x+1<0.25x.
所以当x∈[10,1000]时, 再计算按模型 y=log7x+1奖励时,奖金是否
不超过利润的25%,即当x∈[10,1000]时,是否有 成立. 综上所述,模型y=log7x+1确实能符合公司
要求. 解:模型y=log7x+1奖励时, 奖金不会超过利润的25%.. 说明按归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,认
真审题,理解实际背景.弄清楚问题的实际背
景和意义,设法用数学语言来描述问题.
(2) 简化假设:理解所给的实际问题之后,领
悟背景中反映的实质,需要对问题作必要的
简化,有时要给出一些恰当的假设,精选问题
中关键或主要的变量.
(3) 数学建模:把握新信息,勇于探索,善于联
想,灵活化归,根据题意建立变量或参数间的
数学关系,实现实际问题数学化,引进数学符
号,构建数学模型,常用的数学模型有方程、
不等式、函数.归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,认
真审题,理解实际背景.弄清楚问题的实际背
景和意义,设法用数学语言来描述问题.
(2) 简化假设:理解所给的实际问题之后,领
悟背景中反映的实质,需要对问题作必要的
简化,有时要给出一些恰当的假设,精选问题
中关键或主要的变量.
(3) 数学建模:把握新信息,勇于探索,善于联
想,灵活化归,根据题意建立变量或参数间的
数学关系,实现实际问题数学化,引进数学符
号,构建数学模型,常用的数学模型有方程、
不等式、函数.归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,认
真审题,理解实际背景.弄清楚问题的实际背
景和意义,设法用数学语言来描述问题.
(2) 简化假设:理解所给的实际问题之后,领
悟背景中反映的实质,需要对问题作必要的
简化,有时要给出一些恰当的假设,精选问题
中关键或主要的变量.
(3) 数学建模:把握新信息,勇于探索,善于联
想,灵活化归,根据题意建立变量或参数间的
数学关系,实现实际问题数学化,引进数学符
号,构建数学模型,常用的数学模型有方程、
不等式、函数.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具对建
立的数学模型进行求解.
(5) 检验模型:将所求的结果代回模型之中检
验,对模拟的结果与实际情形比较,以确定
模型的有效性,如果不满意,要考虑重新建
模.
(6) 评价与应用:如果模型与实际情形比较吻
合,要对计算的结果作出解释并给出其实际
意义,后对所建立的模型给出运用范围.如果
模型与实际问题有较大出入,则要对模型改
进并重复上述步骤.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具对建
立的数学模型进行求解.
(5) 检验模型:将所求的结果代回模型之中检
验,对模拟的结果与实际情形比较,以确定
模型的有效性,如果不满意,要考虑重新建
模.
(6) 评价与应用:如果模型与实际情形比较吻
合,要对计算的结果作出解释并给出其实际
意义,后对所建立的模型给出运用范围.如果
模型与实际问题有较大出入,则要对模型改
进并重复上述步骤.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具对建
立的数学模型进行求解.
(5) 检验模型:将所求的结果代回模型之中检
验,对模拟的结果与实际情形比较,以确定
模型的有效性,如果不满意,要考虑重新建
模.
(6) 评价与应用:如果模型与实际情形比较吻
合,要对计算的结果作出解释并给出其实际
意义,后对所建立的模型给出运用范围.如果
模型与实际问题有较大出入,则要对模型改
进并重复上述步骤.归纳总结中学数学建模的主要步骤练习 某皮鞋厂今年1月份开始投产,并且前4
个月的产量分别为1万双,1.2万双,1.3万双,
1.37万双. 由于产品质量好,款式新颖,前几
个月的销售情况良好.为了推销员在推销产品
时,接受定单不至于过多或过少,需要估计
以后几个月的产量. 厂里分析,产量的增加是
由于工人生产熟练和理顺了生产流程. 厂里也
暂时不准备增加设备和工人. 假如你是厂长,
就月份x,产量为y给出四种函数模型:+b,y=abx +c,y=ax+b,y=ax2+bx+c,y=a你将利用哪一种模型去估算以后几个月的产量?课 堂 小 结 理解问题
(2) 简化假设
(3) 数学建模
(4) 求解模型
(5) 检验模型
(6) 评价与应用归纳总结中学数学建模的主要步骤课 后 作 业2. 《习案》作业三十一.1. 阅读教材P.95~ P.98.
的函数模型(一)复 习 引 入讲 授 新 课例1 假设你有一笔资金用于投资,现在有
三种投资方案供你选择,这三种方案的回
报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前
一天多回报10元;
方案三:第一天回报0.4元,以后每天的回
报比前一天翻一番.
请问,你会选择哪种投资方案?解:设第x天所得回报是y元,
解:设第x天所得回报是y元,
则方案一可以用函数y=40(x∈N*)进行描述;解:设第x天所得回报是y元,
则方案一可以用函数y=40(x∈N*)进行描述;
方案二可以用函数y=10x (x∈N*)进行
描述;解:设第x天所得回报是y元,
则方案一可以用函数y=40(x∈N*)进行描述;
方案二可以用函数y=10x (x∈N*)进行
描述;
方案三可以用函数y=0.4×2x-1(x∈N*)
进行描述.20406080100120246810Oyx 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40y=10x 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40y=10xy=0.4×2x-1 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点.20406080100120246810Oyxy=40y=10xy=0.4×2x-1 函数图象是分析问题的好帮
手.为了便于观察,我们用虚线
连接离散的点. 我们看到,底为
2的指数函数模型
比线性函数模型增
长速度要快得多.从中你对“指数爆
炸”的含义有什么
新的理解?
20406080100120246810Oyxy=40y=10x 根据以上的分
析,是否应作这样
的选择: 投资5天以
下选方案一,投资
5~8天选方案二,
投资8天以上选方
案三?y=0.4×2x-1例2 某公司为了实现1000万元利润的目标,
准备制定一个激励销售部门的奖励方案:
在销售利润达到10万元时,按销售利润进
行奖励,且奖金y(单位:万元)随销售利润
x(单位:万元)的增加而增加,但奖金总数
不超过5万元,同时奖金总数不超过利润
的25%,现有三个奖励模型:
y=0.25x, y=log7x+1, y=1.002x,
其中哪个模型能符合公司的要求?分析:某个奖励模型符合公司要求,就是
依据这个模型进行奖励时,奖金总数不超
过5万元,同时奖金不超过利润的25%,
由于公司总的利润目标为1000万元,所以
部门销售利润一般不会超过公司总的利润.
于是,只需在区间[10,1000]上,检验三个
模型是否符合公司要求即可.分析:某个奖励模型符合公司要求,就是
依据这个模型进行奖励时,奖金总数不超
过5万元,同时奖金不超过利润的25%,
由于公司总的利润目标为1000万元,所以
部门销售利润一般不会超过公司总的利润.
于是,只需在区间[10,1000]上,检验三个
模型是否符合公司要求即可. 不妨先作出函数图象,通过观察函数
的图象,得到初步的结论再通过具体计算,
确认结果.812345672004006008001000Oyx图象812345672004006008001000Oyxy=5图象812345672004006008001000y=0.25xOyxy=5图象812345672004006008001000y=0.25xy=log7x+1Oyxy=5图象812345672004006008001000y=0.25xy=log7x+1y=1.002xOyxy=5图象解: 借助计算机作出函数y=0.25x, y=log7x+1,
y=1.002x的图象.观察图象发现,在区间[10,1000]
上,模型y=0.25x,y=1.002x的图象都有一部分在
直线y=5的上方,只有模型y=log7x+1的图象始终
在y=5的下方,这
说明只有按模型
y=log7x+1进行
奖励时才符合公
司的要求,下面
通过计算确认上
述判断. 首选计算哪个模型的奖金总数不超过5万.解: 首选计算哪个模型的奖金总数不超过5万. 对于模型y=0.25x,它在区间[10, 1000]上递增,
而且当x=20时,y=5,因此,当x>20时,y>5,
所以该模型不符合要求;解: 首选计算哪个模型的奖金总数不超过5万. 对于模型y=0.25x,它在区间[10, 1000]上递增,
而且当x=20时,y=5,因此,当x>20时,y>5,
所以该模型不符合要求; 对于模型y=1.002x,由函数图象,并利用计算
器,可知在区间(805, 806) 内有一个点x0满足
1.002x=5,由于它在区间[10,1000]上递增,因此当
x>x0时,y>5,所以该模型也不符合要求;解: 首选计算哪个模型的奖金总数不超过5万. 对于模型y=0.25x,它在区间[10, 1000]上递增,
而且当x=20时,y=5,因此,当x>20时,y>5,
所以该模型不符合要求; 对于模型y=1.002x,由函数图象,并利用计算
器,可知在区间(805, 806) 内有一个点x0满足
1.002x=5,由于它在区间[10,1000]上递增,因此当
x>x0时,y>5,所以该模型也不符合要求; 对于模型y=log7x+1,它在区间[10,1000] 上递
增,而且当x=1000时,y=log71000+1≈4.55<5,
所以它符合奖金总数不超过5万元的要求. 解: 再计算按模型 y=log7x+1奖励时,奖金是否
不超过利润的25%,即当x∈[10,1000]时,是否有 成立.解: 令f(x)=log7x+1-0.25,x∈[10,1000].利用计
算机作出函数f(x)的图象,由图象可知它是递减的,
因此f(x)<f(10)≈-0.3167<0,即log7x+1<0.25x.
所以当x∈[10,1000]时, 再计算按模型 y=log7x+1奖励时,奖金是否
不超过利润的25%,即当x∈[10,1000]时,是否有 成立.解:模型y=log7x+1奖励时, 奖金不会超过利润的25%.. 说明按 令f(x)=log7x+1-0.25,x∈[10,1000].利用计
算机作出函数f(x)的图象,由图象可知它是递减的,
因此f(x)<f(10)≈-0.3167<0,即log7x+1<0.25x.
所以当x∈[10,1000]时, 再计算按模型 y=log7x+1奖励时,奖金是否
不超过利润的25%,即当x∈[10,1000]时,是否有 成立. 综上所述,模型y=log7x+1确实能符合公司
要求. 解:模型y=log7x+1奖励时, 奖金不会超过利润的25%.. 说明按归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,认
真审题,理解实际背景.弄清楚问题的实际背
景和意义,设法用数学语言来描述问题.
(2) 简化假设:理解所给的实际问题之后,领
悟背景中反映的实质,需要对问题作必要的
简化,有时要给出一些恰当的假设,精选问题
中关键或主要的变量.
(3) 数学建模:把握新信息,勇于探索,善于联
想,灵活化归,根据题意建立变量或参数间的
数学关系,实现实际问题数学化,引进数学符
号,构建数学模型,常用的数学模型有方程、
不等式、函数.归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,认
真审题,理解实际背景.弄清楚问题的实际背
景和意义,设法用数学语言来描述问题.
(2) 简化假设:理解所给的实际问题之后,领
悟背景中反映的实质,需要对问题作必要的
简化,有时要给出一些恰当的假设,精选问题
中关键或主要的变量.
(3) 数学建模:把握新信息,勇于探索,善于联
想,灵活化归,根据题意建立变量或参数间的
数学关系,实现实际问题数学化,引进数学符
号,构建数学模型,常用的数学模型有方程、
不等式、函数.归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,认
真审题,理解实际背景.弄清楚问题的实际背
景和意义,设法用数学语言来描述问题.
(2) 简化假设:理解所给的实际问题之后,领
悟背景中反映的实质,需要对问题作必要的
简化,有时要给出一些恰当的假设,精选问题
中关键或主要的变量.
(3) 数学建模:把握新信息,勇于探索,善于联
想,灵活化归,根据题意建立变量或参数间的
数学关系,实现实际问题数学化,引进数学符
号,构建数学模型,常用的数学模型有方程、
不等式、函数.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具对建
立的数学模型进行求解.
(5) 检验模型:将所求的结果代回模型之中检
验,对模拟的结果与实际情形比较,以确定
模型的有效性,如果不满意,要考虑重新建
模.
(6) 评价与应用:如果模型与实际情形比较吻
合,要对计算的结果作出解释并给出其实际
意义,后对所建立的模型给出运用范围.如果
模型与实际问题有较大出入,则要对模型改
进并重复上述步骤.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具对建
立的数学模型进行求解.
(5) 检验模型:将所求的结果代回模型之中检
验,对模拟的结果与实际情形比较,以确定
模型的有效性,如果不满意,要考虑重新建
模.
(6) 评价与应用:如果模型与实际情形比较吻
合,要对计算的结果作出解释并给出其实际
意义,后对所建立的模型给出运用范围.如果
模型与实际问题有较大出入,则要对模型改
进并重复上述步骤.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具对建
立的数学模型进行求解.
(5) 检验模型:将所求的结果代回模型之中检
验,对模拟的结果与实际情形比较,以确定
模型的有效性,如果不满意,要考虑重新建
模.
(6) 评价与应用:如果模型与实际情形比较吻
合,要对计算的结果作出解释并给出其实际
意义,后对所建立的模型给出运用范围.如果
模型与实际问题有较大出入,则要对模型改
进并重复上述步骤.归纳总结中学数学建模的主要步骤练习 某皮鞋厂今年1月份开始投产,并且前4
个月的产量分别为1万双,1.2万双,1.3万双,
1.37万双. 由于产品质量好,款式新颖,前几
个月的销售情况良好.为了推销员在推销产品
时,接受定单不至于过多或过少,需要估计
以后几个月的产量. 厂里分析,产量的增加是
由于工人生产熟练和理顺了生产流程. 厂里也
暂时不准备增加设备和工人. 假如你是厂长,
就月份x,产量为y给出四种函数模型:+b,y=abx +c,y=ax+b,y=ax2+bx+c,y=a你将利用哪一种模型去估算以后几个月的产量?课 堂 小 结 理解问题
(2) 简化假设
(3) 数学建模
(4) 求解模型
(5) 检验模型
(6) 评价与应用归纳总结中学数学建模的主要步骤课 后 作 业2. 《习案》作业三十一.1. 阅读教材P.95~ P.98.
