高中人教A版数学3.2.1几类不同增长的函数模型(二)ppt课件
文档属性
| 名称 | 高中人教A版数学3.2.1几类不同增长的函数模型(二)ppt课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 86.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-13 00:00:00 | ||
图片预览











文档简介
课件39张PPT。3.2.1几类不同增长
的函数模型(二)复 习 引 入归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,
认真审题,理解实际背景. 弄清楚问题的
实际背景和意义,设法用数学语言来描述
问题.
(2) 简化假设:理解所给的实际问题之后,
领悟背景中反映的实质,需要对问题作必
要的简化,有时要给出一些恰当的假设,
精选问题中关键或主要的变量.复 习 引 入归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,
认真审题,理解实际背景. 弄清楚问题的
实际背景和意义,设法用数学语言来描述
问题.
(2) 简化假设:理解所给的实际问题之后,
领悟背景中反映的实质,需要对问题作必
要的简化,有时要给出一些恰当的假设,
精选问题中关键或主要的变量.复 习 引 入归纳总结中学数学建模的主要步骤复 习 引 入(3) 数学建模:把握新信息,勇于探索,
善于联想,灵活化归,根据题意建立变
量或参数间的数学关系,实现实际问题
数学化,引进数学符号,构建数学模型,
常用的数学模型有方程、不等式、函数.归纳总结中学数学建模的主要步骤复 习 引 入(3) 数学建模:把握新信息,勇于探索,
善于联想,灵活化归,根据题意建立变
量或参数间的数学关系,实现实际问题
数学化,引进数学符号,构建数学模型,
常用的数学模型有方程、不等式、函数.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具
对建立的数学模型进行求解.(5) 检验模型:将所求的结果代回模型之
中检验,对模拟的结果与实际情形比较,
以确定模型的有效性,如果不满意,要
考虑重新建模.
(6) 评价与应用:如果模型与实际情形比
较吻合,要对计算的结果作出解释并给
出其实际意义,后对所建立的模型给出
运用范围.如果模型与实际问题有较大出
入,则要对模型改进并重复上述步骤.复 习 引 入归纳总结中学数学建模的主要步骤(5) 检验模型:将所求的结果代回模型之
中检验,对模拟的结果与实际情形比较,
以确定模型的有效性,如果不满意,要
考虑重新建模.
(6) 评价与应用:如果模型与实际情形比
较吻合,要对计算的结果作出解释并给
出其实际意义,后对所建立的模型给出
运用范围.如果模型与实际问题有较大出
入,则要对模型改进并重复上述步骤.复 习 引 入归纳总结中学数学建模的主要步骤 理解问题
(2) 简化假设
(3) 数学建模
(4) 求解模型
(5) 检验模型
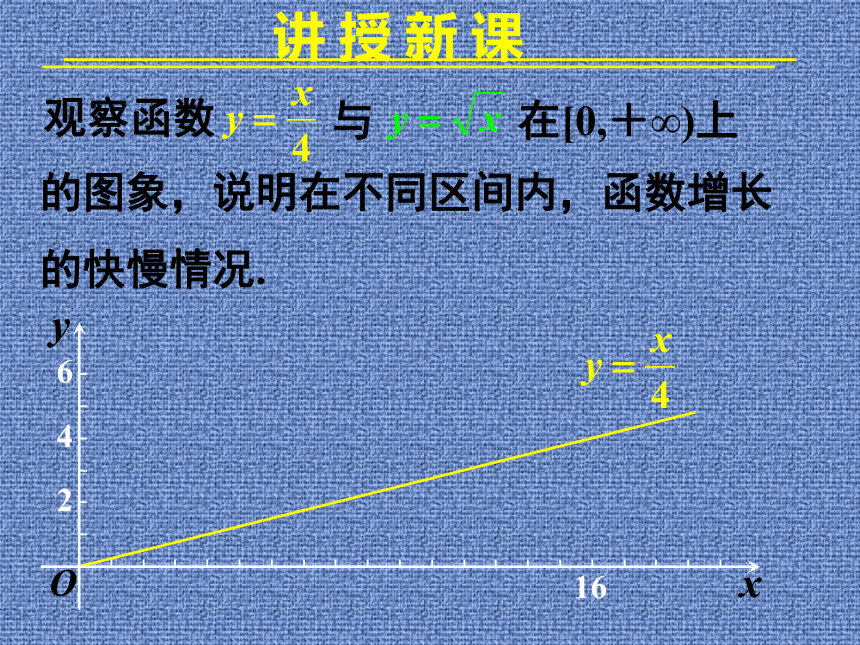
(6) 评价与应用归纳总结中学数学建模的主要步骤讲 授 新 课观察函数与的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上比较函数的增长快慢.比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO你能分别求出使成立的x的取值
范围吗?30282624222018161412108642510xyO放大后
的图象① 一般地,对于指数函数y=ax(a>1)和
幂函数y=xn(n>0),在区间(0, +∞)上,
无论n比a大多少,尽管在x的一定变化范
围内,ax会小于xn,但由于ax的增长快于
xn的增长,因此总存在一个x0,当x>x0
时,就会有ax>xn.规律总结②对于对数函数y=logax (a>1)和幂函数
y=xn(n>0)在区间(0, +∞)上,随着x的
增大,logax增长得越来越慢.在x的一定
变化范围内,logax可能会大于xn,但由
于logax的增长慢于xn的增长,因此总存
在一个x0,当x>x0时,就会有logax<xn.规律总结③在区间(0, +∞)上,尽管函数y=ax
(a>1),y=logax(a>1)和y = xn(n>0)
都是增函数,但它们的增长速度不同,
而且不在同一个“档次”上.随着x的增
长,y=ax(a>1)的增长速度越来越快,
会超过并远远大于y=xn(n>0)的增长
速度,而y=logax(a>1)的增长速度则
会越来越慢.因此,总会存在一个x0,
当x>x0时,就有logax<xn<ax.规律总结例1 同一坐标系中,函数
y=x2+7和y=2x的图象
如图.试比较x2+7与2x的
大小.5040302010510y=x2+7y=2xxyO例2 已知函数y=x2和y=log2(x+1)的图象
如图,试比较x2与log2(x+1)的大小.4321-124xyOy=x2y=log2(x+1)1. 下列说法不正确的是 ( C ) A. 函数y=2x在(0,+∞)上是增函数
B. 函数y=x2在(0,+∞)上是增函数
C. 存在x0,当x>x0时,x2>2x恒成立
D. 存在x0,当x>x0时,2x>x2恒成立练习1. 下列说法不正确的是 ( C ) A. 函数y=2x在(0,+∞)上是增函数
B. 函数y=x2在(0,+∞)上是增函数
C. 存在x0,当x>x0时,x2>2x恒成立
D. 存在x0,当x>x0时,2x>x2恒成立练习2.比较函数y=xn(n>0)和y=ax(a>0),
下列说法正确的是 ( B ) A. 函数y=xn比y=ax的增长速度快
B. 函数y=xn比y=ax的增长速度慢
C. 因a, n没有大小确定, 故无法比较函数
y=xn与y=ax的增长速度
D. 以上都不正确 练习2.比较函数y=xn(n>0)和y=ax(a>0),
下列说法正确的是 ( B ) A. 函数y=xn比y=ax的增长速度快
B. 函数y=xn比y=ax的增长速度慢
C. 因a, n没有大小确定, 故无法比较函数
y=xn与y=ax的增长速度
D. 以上都不正确 练习3. 函数y=logax(a>1)、y=bx(b>1)和
y=xc(c>0)中增长速度最快的是( B )A. y=logax(a>1) B. y=bx(b>1)
C. y=xc(c>0) D. 无法确定练习3. 函数y=logax(a>1)、y=bx(b>1)和
y=xc(c>0)中增长速度最快的是( B )A. y=logax(a>1) B. y=bx(b>1)
C. y=xc(c>0) D. 无法确定练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.5432124xyOABC练习y=2x5432124xyOABC练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.5432124xyOABC练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.y=2xy=x1.4y=2xy=x1.45432124xyOABCy=lnx练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.课 堂 小 结1. 幂函数、指数函数、对数函数增长
快慢的差异;
课 堂 小 结1. 幂函数、指数函数、对数函数增长
快慢的差异;
2. 直线上升、指数爆炸、对数增长
等不同函数类型增长的含义.课 后 作 业2. 《习案》作业三十二.1. 阅读教材P.98~ P.101.
的函数模型(二)复 习 引 入归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,
认真审题,理解实际背景. 弄清楚问题的
实际背景和意义,设法用数学语言来描述
问题.
(2) 简化假设:理解所给的实际问题之后,
领悟背景中反映的实质,需要对问题作必
要的简化,有时要给出一些恰当的假设,
精选问题中关键或主要的变量.复 习 引 入归纳总结中学数学建模的主要步骤(1) 理解问题:阅读理解,读懂文字叙述,
认真审题,理解实际背景. 弄清楚问题的
实际背景和意义,设法用数学语言来描述
问题.
(2) 简化假设:理解所给的实际问题之后,
领悟背景中反映的实质,需要对问题作必
要的简化,有时要给出一些恰当的假设,
精选问题中关键或主要的变量.复 习 引 入归纳总结中学数学建模的主要步骤复 习 引 入(3) 数学建模:把握新信息,勇于探索,
善于联想,灵活化归,根据题意建立变
量或参数间的数学关系,实现实际问题
数学化,引进数学符号,构建数学模型,
常用的数学模型有方程、不等式、函数.归纳总结中学数学建模的主要步骤复 习 引 入(3) 数学建模:把握新信息,勇于探索,
善于联想,灵活化归,根据题意建立变
量或参数间的数学关系,实现实际问题
数学化,引进数学符号,构建数学模型,
常用的数学模型有方程、不等式、函数.归纳总结中学数学建模的主要步骤(4) 求解模型:以所学的数学性质为工具
对建立的数学模型进行求解.(5) 检验模型:将所求的结果代回模型之
中检验,对模拟的结果与实际情形比较,
以确定模型的有效性,如果不满意,要
考虑重新建模.
(6) 评价与应用:如果模型与实际情形比
较吻合,要对计算的结果作出解释并给
出其实际意义,后对所建立的模型给出
运用范围.如果模型与实际问题有较大出
入,则要对模型改进并重复上述步骤.复 习 引 入归纳总结中学数学建模的主要步骤(5) 检验模型:将所求的结果代回模型之
中检验,对模拟的结果与实际情形比较,
以确定模型的有效性,如果不满意,要
考虑重新建模.
(6) 评价与应用:如果模型与实际情形比
较吻合,要对计算的结果作出解释并给
出其实际意义,后对所建立的模型给出
运用范围.如果模型与实际问题有较大出
入,则要对模型改进并重复上述步骤.复 习 引 入归纳总结中学数学建模的主要步骤 理解问题
(2) 简化假设
(3) 数学建模
(4) 求解模型
(5) 检验模型
(6) 评价与应用归纳总结中学数学建模的主要步骤讲 授 新 课观察函数与的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上讲 授 新 课观察函数与64216xyO的图象,说明在不同区间内,函数增长
的快慢情况.在[0,+∞)上比较函数的增长快慢.比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO比较函数的增长快慢.8642-22468xyO你能分别求出使成立的x的取值
范围吗?30282624222018161412108642510xyO放大后
的图象① 一般地,对于指数函数y=ax(a>1)和
幂函数y=xn(n>0),在区间(0, +∞)上,
无论n比a大多少,尽管在x的一定变化范
围内,ax会小于xn,但由于ax的增长快于
xn的增长,因此总存在一个x0,当x>x0
时,就会有ax>xn.规律总结②对于对数函数y=logax (a>1)和幂函数
y=xn(n>0)在区间(0, +∞)上,随着x的
增大,logax增长得越来越慢.在x的一定
变化范围内,logax可能会大于xn,但由
于logax的增长慢于xn的增长,因此总存
在一个x0,当x>x0时,就会有logax<xn.规律总结③在区间(0, +∞)上,尽管函数y=ax
(a>1),y=logax(a>1)和y = xn(n>0)
都是增函数,但它们的增长速度不同,
而且不在同一个“档次”上.随着x的增
长,y=ax(a>1)的增长速度越来越快,
会超过并远远大于y=xn(n>0)的增长
速度,而y=logax(a>1)的增长速度则
会越来越慢.因此,总会存在一个x0,
当x>x0时,就有logax<xn<ax.规律总结例1 同一坐标系中,函数
y=x2+7和y=2x的图象
如图.试比较x2+7与2x的
大小.5040302010510y=x2+7y=2xxyO例2 已知函数y=x2和y=log2(x+1)的图象
如图,试比较x2与log2(x+1)的大小.4321-124xyOy=x2y=log2(x+1)1. 下列说法不正确的是 ( C ) A. 函数y=2x在(0,+∞)上是增函数
B. 函数y=x2在(0,+∞)上是增函数
C. 存在x0,当x>x0时,x2>2x恒成立
D. 存在x0,当x>x0时,2x>x2恒成立练习1. 下列说法不正确的是 ( C ) A. 函数y=2x在(0,+∞)上是增函数
B. 函数y=x2在(0,+∞)上是增函数
C. 存在x0,当x>x0时,x2>2x恒成立
D. 存在x0,当x>x0时,2x>x2恒成立练习2.比较函数y=xn(n>0)和y=ax(a>0),
下列说法正确的是 ( B ) A. 函数y=xn比y=ax的增长速度快
B. 函数y=xn比y=ax的增长速度慢
C. 因a, n没有大小确定, 故无法比较函数
y=xn与y=ax的增长速度
D. 以上都不正确 练习2.比较函数y=xn(n>0)和y=ax(a>0),
下列说法正确的是 ( B ) A. 函数y=xn比y=ax的增长速度快
B. 函数y=xn比y=ax的增长速度慢
C. 因a, n没有大小确定, 故无法比较函数
y=xn与y=ax的增长速度
D. 以上都不正确 练习3. 函数y=logax(a>1)、y=bx(b>1)和
y=xc(c>0)中增长速度最快的是( B )A. y=logax(a>1) B. y=bx(b>1)
C. y=xc(c>0) D. 无法确定练习3. 函数y=logax(a>1)、y=bx(b>1)和
y=xc(c>0)中增长速度最快的是( B )A. y=logax(a>1) B. y=bx(b>1)
C. y=xc(c>0) D. 无法确定练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.5432124xyOABC练习y=2x5432124xyOABC练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.5432124xyOABC练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.y=2xy=x1.4y=2xy=x1.45432124xyOABCy=lnx练习4.已知幂函数y=x1.4、指数y=2x和对数
函数y=lnx的图象.
如图,则A表示函数
的图象,
B表示函数 .
的图象,C表示函
数 的图象.课 堂 小 结1. 幂函数、指数函数、对数函数增长
快慢的差异;
课 堂 小 结1. 幂函数、指数函数、对数函数增长
快慢的差异;
2. 直线上升、指数爆炸、对数增长
等不同函数类型增长的含义.课 后 作 业2. 《习案》作业三十二.1. 阅读教材P.98~ P.101.
