第五章《抛体运动》学习活动设计五:平抛运动的规律是什么(word版教案)
文档属性
| 名称 | 第五章《抛体运动》学习活动设计五:平抛运动的规律是什么(word版教案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-10 11:09:39 | ||
图片预览


文档简介
第五章《抛体运动》学习活动设计五:平抛运动的规律是什么
【情境创设】观察女排比赛发球的几个片段:水平发出的排球一个没过网、一个出界、一个成功。
【学习任务一】平抛运动的物体任意时刻距抛出点的位移
教师:前面的学习我们知道,在不考虑空气阻力的情况下,水平发出的排球在落地前的运动可以看作平抛运动。
学生总结:由上节课知道,平抛运动可以分解为水平方向和竖直方向的两个分运动,水平方向不受力,排球在水平方向没有加速度,所以在水平方向做匀速直线运动;竖直方向上物体的初速度为0,且只受重力作用,所以在竖直方向上物体做自由落体运动。
提问:做平抛运动的排球有的没过网、有的出界了、有的成功了,说明排球落地的位置不一样,我们在实际平抛运动的研究中往往还需要知道物体在空中某一时刻的位置。同学们思考,我们如何确定平抛运动的排球某一时刻的位置?
学生思考、交流。
学生回答:在机械运动中我们学过,确定物体的位置及位置的变化时需要建立坐标系,在这里我们也需要建立坐标系。
教师总结:平抛运动是在一个平面内的曲线运动,我们应该建立平面直角坐标系。
提问:如何建立平面直角坐标系呢?
学生回答:因为初速度水平,只受竖直方向的重力作用,所以我们以排球抛出点为坐标原点;以水平抛出的方向为轴的方向,竖直向下的方向为轴的方向,建立坐标系(如图),
教师:设排球水平抛出瞬间的速度为,经过时间t水平位移是多少?
学生回答:水平方向是匀速直线运动,所以水平位移应该是。
教师提问:竖直位移呢?
学生回答:竖直方向做的是自由落体运动,竖直位移。
教师总结:这里(x,y)就是t时刻物体所在的位置。
提问:那么如何求合位移呢?
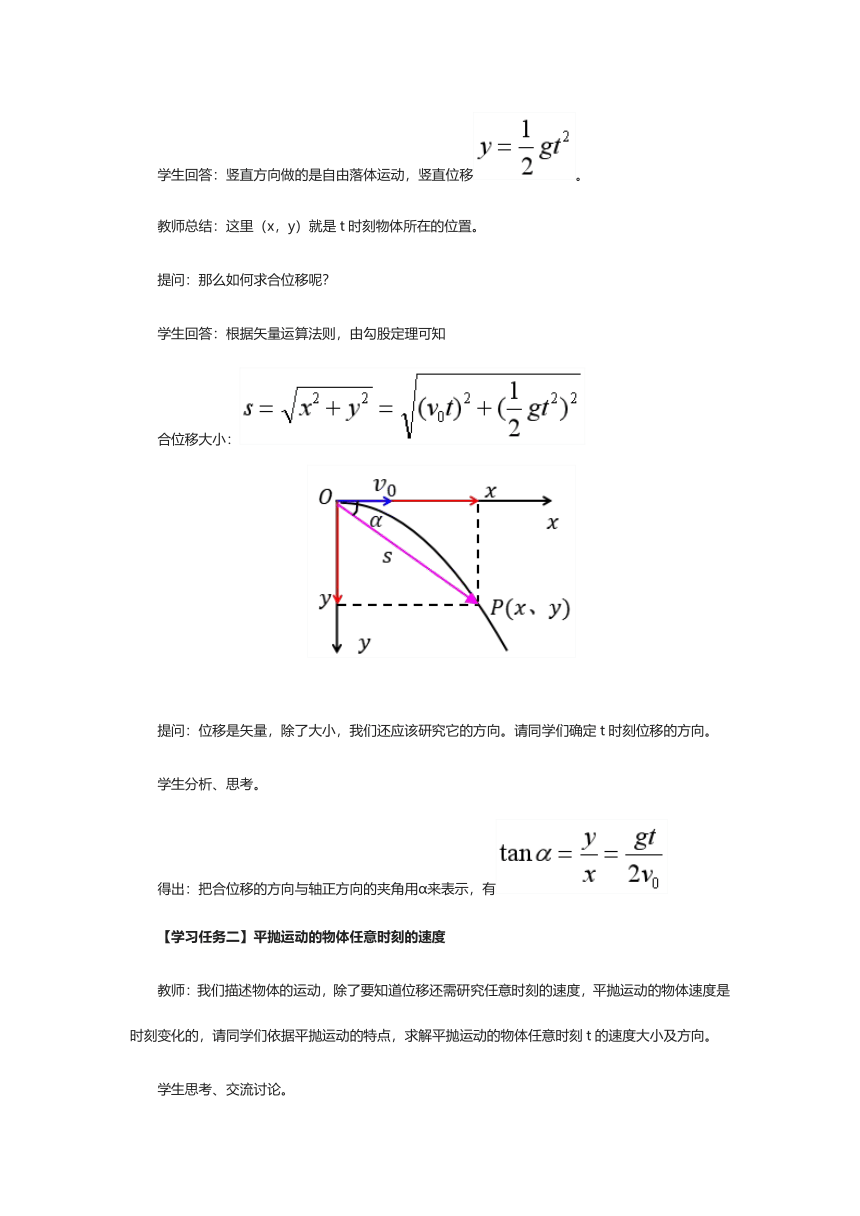
学生回答:根据矢量运算法则,由勾股定理可知
合位移大小:
提问:位移是矢量,除了大小,我们还应该研究它的方向。请同学们确定t时刻位移的方向。
学生分析、思考。
得出:把合位移的方向与轴正方向的夹角用α来表示,有
【学习任务二】平抛运动的物体任意时刻的速度
教师:我们描述物体的运动,除了要知道位移还需研究任意时刻的速度,平抛运动的物体速度是时刻变化的,请同学们依据平抛运动的特点,求解平抛运动的物体任意时刻t的速度大小及方向。
学生思考、交流讨论。
得出:平抛运动的物体,任意时刻水平分速度
竖直分速度
合速度的大小:
合速度的方向:
合速度与轴正方向夹角用来表示:
提问:合位移与轴正方向的夹角α和合速度与轴正方向夹角相同吗?
学生总结:根据,所以,任意时刻合位移与轴正方向夹角的正切值是合速度与轴正方向夹角正切值的一半。
提问:我们在上图中看到t时刻物体速度的反向延长线交在轴上,设交点的横坐标为,同学们讨论一下,这个交点有什么特点?
同学讨论。
得出:由图知
将、代入,得
所以任意时刻t合速度的反向延长线交于0~t时间内水平位移的中点。
提问:我们刚开始看到的排球平抛运动的轨迹是曲线,这和我们数学中的某一种曲线是不是有相似之处呢?
同学回答:像抛物线!
提问:请同学们推导一下y与x的关系是怎样的?
学生推导:物体以速度水平抛出
从中解出,代入式,得到
教师:由y与x的关系式,你又能得出什么结论?
学生:式中g、都是与x、y无关的常量,所以也是常量。这正是数学中的抛物线方程,二次函数的图象是一条抛物线!
教师:“抛物线”的名称就是这样得来的。
教师:分析得出平抛物体运动的轨迹是一条抛物线。同学们课下可以继续研究“学习活动设计四中的学习评价自测第1题”得到的钢球的运动轨迹,看看是否为一条抛物线。
【学习小结】
【学习评价自测】
1.用枪水平瞄准射击一个靶子,子弹从枪口水平射出的瞬间,靶子从静止开始自由下落。设靶子足够高,不计空气阻力。则下列说法正确的是( )
A.子弹一定打不到靶子上
B.子弹打到靶子上的位置应在瞄准点的上方一些
C.子弹打到靶子上的位置应落在瞄准点上
D.子弹能否打到靶子上取决于靶子的大小和子弹的初速度
答案:C
2.排球网高约d=2.0m,设运动员发球的高度为h=3.0m,排球场的半场长L=9m,要想发球能过网,水平发球的速度不能小于多少?
答案:约72.5km/h
【情境创设】观察女排比赛发球的几个片段:水平发出的排球一个没过网、一个出界、一个成功。
【学习任务一】平抛运动的物体任意时刻距抛出点的位移
教师:前面的学习我们知道,在不考虑空气阻力的情况下,水平发出的排球在落地前的运动可以看作平抛运动。
学生总结:由上节课知道,平抛运动可以分解为水平方向和竖直方向的两个分运动,水平方向不受力,排球在水平方向没有加速度,所以在水平方向做匀速直线运动;竖直方向上物体的初速度为0,且只受重力作用,所以在竖直方向上物体做自由落体运动。
提问:做平抛运动的排球有的没过网、有的出界了、有的成功了,说明排球落地的位置不一样,我们在实际平抛运动的研究中往往还需要知道物体在空中某一时刻的位置。同学们思考,我们如何确定平抛运动的排球某一时刻的位置?
学生思考、交流。
学生回答:在机械运动中我们学过,确定物体的位置及位置的变化时需要建立坐标系,在这里我们也需要建立坐标系。
教师总结:平抛运动是在一个平面内的曲线运动,我们应该建立平面直角坐标系。
提问:如何建立平面直角坐标系呢?
学生回答:因为初速度水平,只受竖直方向的重力作用,所以我们以排球抛出点为坐标原点;以水平抛出的方向为轴的方向,竖直向下的方向为轴的方向,建立坐标系(如图),
教师:设排球水平抛出瞬间的速度为,经过时间t水平位移是多少?
学生回答:水平方向是匀速直线运动,所以水平位移应该是。
教师提问:竖直位移呢?
学生回答:竖直方向做的是自由落体运动,竖直位移。
教师总结:这里(x,y)就是t时刻物体所在的位置。
提问:那么如何求合位移呢?
学生回答:根据矢量运算法则,由勾股定理可知
合位移大小:
提问:位移是矢量,除了大小,我们还应该研究它的方向。请同学们确定t时刻位移的方向。
学生分析、思考。
得出:把合位移的方向与轴正方向的夹角用α来表示,有
【学习任务二】平抛运动的物体任意时刻的速度
教师:我们描述物体的运动,除了要知道位移还需研究任意时刻的速度,平抛运动的物体速度是时刻变化的,请同学们依据平抛运动的特点,求解平抛运动的物体任意时刻t的速度大小及方向。
学生思考、交流讨论。
得出:平抛运动的物体,任意时刻水平分速度
竖直分速度
合速度的大小:
合速度的方向:
合速度与轴正方向夹角用来表示:
提问:合位移与轴正方向的夹角α和合速度与轴正方向夹角相同吗?
学生总结:根据,所以,任意时刻合位移与轴正方向夹角的正切值是合速度与轴正方向夹角正切值的一半。
提问:我们在上图中看到t时刻物体速度的反向延长线交在轴上,设交点的横坐标为,同学们讨论一下,这个交点有什么特点?
同学讨论。
得出:由图知
将、代入,得
所以任意时刻t合速度的反向延长线交于0~t时间内水平位移的中点。
提问:我们刚开始看到的排球平抛运动的轨迹是曲线,这和我们数学中的某一种曲线是不是有相似之处呢?
同学回答:像抛物线!
提问:请同学们推导一下y与x的关系是怎样的?
学生推导:物体以速度水平抛出
从中解出,代入式,得到
教师:由y与x的关系式,你又能得出什么结论?
学生:式中g、都是与x、y无关的常量,所以也是常量。这正是数学中的抛物线方程,二次函数的图象是一条抛物线!
教师:“抛物线”的名称就是这样得来的。
教师:分析得出平抛物体运动的轨迹是一条抛物线。同学们课下可以继续研究“学习活动设计四中的学习评价自测第1题”得到的钢球的运动轨迹,看看是否为一条抛物线。
【学习小结】
【学习评价自测】
1.用枪水平瞄准射击一个靶子,子弹从枪口水平射出的瞬间,靶子从静止开始自由下落。设靶子足够高,不计空气阻力。则下列说法正确的是( )
A.子弹一定打不到靶子上
B.子弹打到靶子上的位置应在瞄准点的上方一些
C.子弹打到靶子上的位置应落在瞄准点上
D.子弹能否打到靶子上取决于靶子的大小和子弹的初速度
答案:C
2.排球网高约d=2.0m,设运动员发球的高度为h=3.0m,排球场的半场长L=9m,要想发球能过网,水平发球的速度不能小于多少?
答案:约72.5km/h
