幂的运算复习课件
图片预览






文档简介
课件16张PPT。8.1 幂的运算复习1、同底数幂乘法的性质及逆运算的应用。
2、同底数幂除法的性质及逆运算的应用。
3、幂的乘方与积的乘方的性质及逆运算的应用。
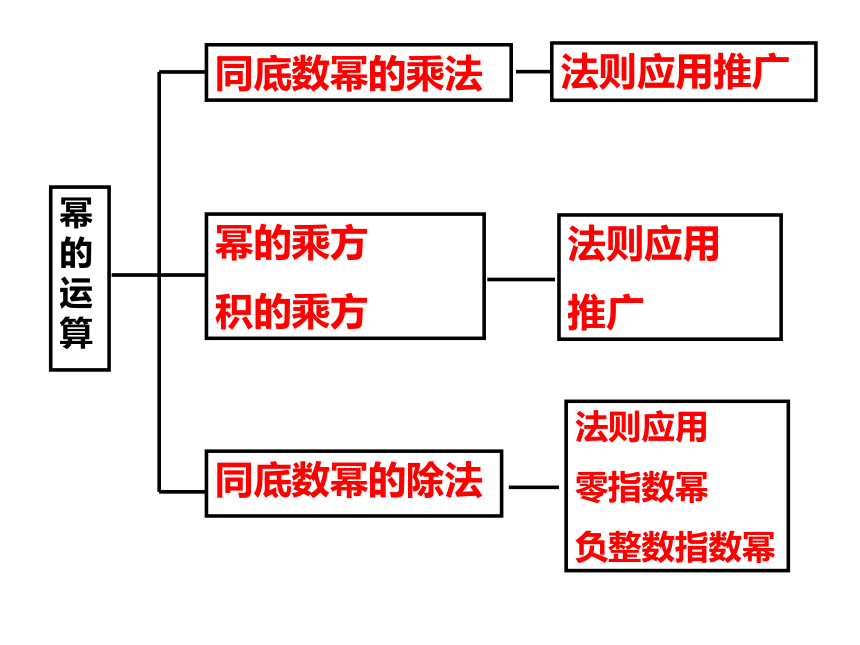
4、在计算过程注意运算顺序及符号。复习目标幂的运算同底数幂的乘法幂的乘方
积的乘方同底数幂的除法法则应用推广法则应用
推广法则应用
零指数幂
负整数指数幂一、回顾交流,系统归纳2.同底数相除,_____ 不变,指数_________. 用式子表示为am÷an=_______. (a≠0, m、n是整数 )
逆用1.同底数相乘,____ 不变,指数______.
用式子表示为am·an=_______.
逆用am+n ( m、n是整数 )底数相减am-n底数相加am+n= am·anam-n= am÷an注意(1) 同底数幂的乘法中,首先要找出相同的底数,运算时,底数不变,直接把指数相加.
(2)如果底数不同,应先设法将其转化为相同的底数,再按法则进行计算.4.积的乘方_______________________.
用式子表示为(ab)n=_______. (n是整数)
逆用3.幂的乘方,_____不变,指数_______.
用式子表示为(am)n=_______. (m、n是整数)
逆用底数amn等于积里每个因式的乘方的积an bn相乘amn= (am)n=(an)man bn= (ab)n 注意:(1)幂的乘方的底数是指幂的底数a,而不是指乘方的底数am;
(2)注意与同底数幂相乘中“指数相加”区分开.
注意:(1) 运用积的乘方法则时,数字系数的乘方,应根据乘方的意义计算出结果;
(2) 运用积的乘方法则时,应把每一个因式都分别乘方,不要遗漏其中任何一个因式 .5.零指数: 当a≠0时,a0= _____. (a≠0)6.负指数:当a≠0时,a-p=______. (a≠0, p是正整数 ) 说明:上面有关“幂的运算”适用幂的乘、除及乘方运算,而有关幂的加、减法运算,要根据合并同类项法则进行计算。
1(a≠0, b≠0, n是正整数 )只要底数不为0,任何数的零次方都等于1. 误区警示,排忧解难.
1.你知道下列各式错在哪里吗?交流反馈①②③④⑤⑥⑦⑧师生探究例1 计算(3)(4)填一填:(并说出运算依据)合并同类项法则幂的乘方法则逆用同底数幂的除法法则逆用同底数幂的乘法法则逆用二、逆向思维. 例2 计算: (2)求:53m 的值。例3 若5m=-2,5n=3.
(1)求:5m+n 的值。解: 5m+n=5m·5n=-2×3=-6解: 53m=(5m)3=(-2)3=-8 (3)求:5-2n 的值。解:变式1 若5m=-2,5n=3. (1)求:53m+52n 的值 解: 53m+2n=53m·52n=(5m)3·(5n)2
=(-2)3×32=-8×9=-72 解:53m+52n=(5m)3+(5n)2=(-2)3+32
=-8+9=1(2)求:53m+2n 的值。(3)求:53m-2n 的值。解:53m-2n=53m÷52n=(5m)3÷ (5n)2
=(-2)3÷32=变式2 若3m+2n-4=0. 求:8m·4n 的值。解: 由3m+2n-4=0,得3m+2n=4,
8m·4n=(23)m· (22)n= 23m·22n
=23m+2n=24=16
学会方法,融会贯通.
计算:P557、8
课堂检测课堂小结本节课你有哪些收获? 你还有哪些困惑?
2、同底数幂除法的性质及逆运算的应用。
3、幂的乘方与积的乘方的性质及逆运算的应用。
4、在计算过程注意运算顺序及符号。复习目标幂的运算同底数幂的乘法幂的乘方
积的乘方同底数幂的除法法则应用推广法则应用
推广法则应用
零指数幂
负整数指数幂一、回顾交流,系统归纳2.同底数相除,_____ 不变,指数_________. 用式子表示为am÷an=_______. (a≠0, m、n是整数 )
逆用1.同底数相乘,____ 不变,指数______.
用式子表示为am·an=_______.
逆用am+n ( m、n是整数 )底数相减am-n底数相加am+n= am·anam-n= am÷an注意(1) 同底数幂的乘法中,首先要找出相同的底数,运算时,底数不变,直接把指数相加.
(2)如果底数不同,应先设法将其转化为相同的底数,再按法则进行计算.4.积的乘方_______________________.
用式子表示为(ab)n=_______. (n是整数)
逆用3.幂的乘方,_____不变,指数_______.
用式子表示为(am)n=_______. (m、n是整数)
逆用底数amn等于积里每个因式的乘方的积an bn相乘amn= (am)n=(an)man bn= (ab)n 注意:(1)幂的乘方的底数是指幂的底数a,而不是指乘方的底数am;
(2)注意与同底数幂相乘中“指数相加”区分开.
注意:(1) 运用积的乘方法则时,数字系数的乘方,应根据乘方的意义计算出结果;
(2) 运用积的乘方法则时,应把每一个因式都分别乘方,不要遗漏其中任何一个因式 .5.零指数: 当a≠0时,a0= _____. (a≠0)6.负指数:当a≠0时,a-p=______. (a≠0, p是正整数 ) 说明:上面有关“幂的运算”适用幂的乘、除及乘方运算,而有关幂的加、减法运算,要根据合并同类项法则进行计算。
1(a≠0, b≠0, n是正整数 )只要底数不为0,任何数的零次方都等于1. 误区警示,排忧解难.
1.你知道下列各式错在哪里吗?交流反馈①②③④⑤⑥⑦⑧师生探究例1 计算(3)(4)填一填:(并说出运算依据)合并同类项法则幂的乘方法则逆用同底数幂的除法法则逆用同底数幂的乘法法则逆用二、逆向思维. 例2 计算: (2)求:53m 的值。例3 若5m=-2,5n=3.
(1)求:5m+n 的值。解: 5m+n=5m·5n=-2×3=-6解: 53m=(5m)3=(-2)3=-8 (3)求:5-2n 的值。解:变式1 若5m=-2,5n=3. (1)求:53m+52n 的值 解: 53m+2n=53m·52n=(5m)3·(5n)2
=(-2)3×32=-8×9=-72 解:53m+52n=(5m)3+(5n)2=(-2)3+32
=-8+9=1(2)求:53m+2n 的值。(3)求:53m-2n 的值。解:53m-2n=53m÷52n=(5m)3÷ (5n)2
=(-2)3÷32=变式2 若3m+2n-4=0. 求:8m·4n 的值。解: 由3m+2n-4=0,得3m+2n=4,
8m·4n=(23)m· (22)n= 23m·22n
=23m+2n=24=16
学会方法,融会贯通.
计算:P557、8
课堂检测课堂小结本节课你有哪些收获? 你还有哪些困惑?
