《第三章 相互作用──力》学习活动设计七:实际问题中力的分解(word版教案)
文档属性
| 名称 | 《第三章 相互作用──力》学习活动设计七:实际问题中力的分解(word版教案) |

|
|
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览



文档简介
《第三章 相互作用──力》学习活动设计七:实际问题中力的分解
课前准备:回忆之前学过的力的合成与分解的基本知识
1.什么是合力、分力?合力与分力有什么关系?
2.什么是力的合成?力的分解?
3.力的合成与分解遵循什么法则?
4.一个力可以有多少种分解方法?如何确定唯一的解?
课堂教学:
【任务情景】
小明独自驾车陷入淤泥,路旁有很多大树(如图1所示),后备箱中只有一根足够长的粗绳,你能给他出个主意拉出汽车吗?
【教学策略】
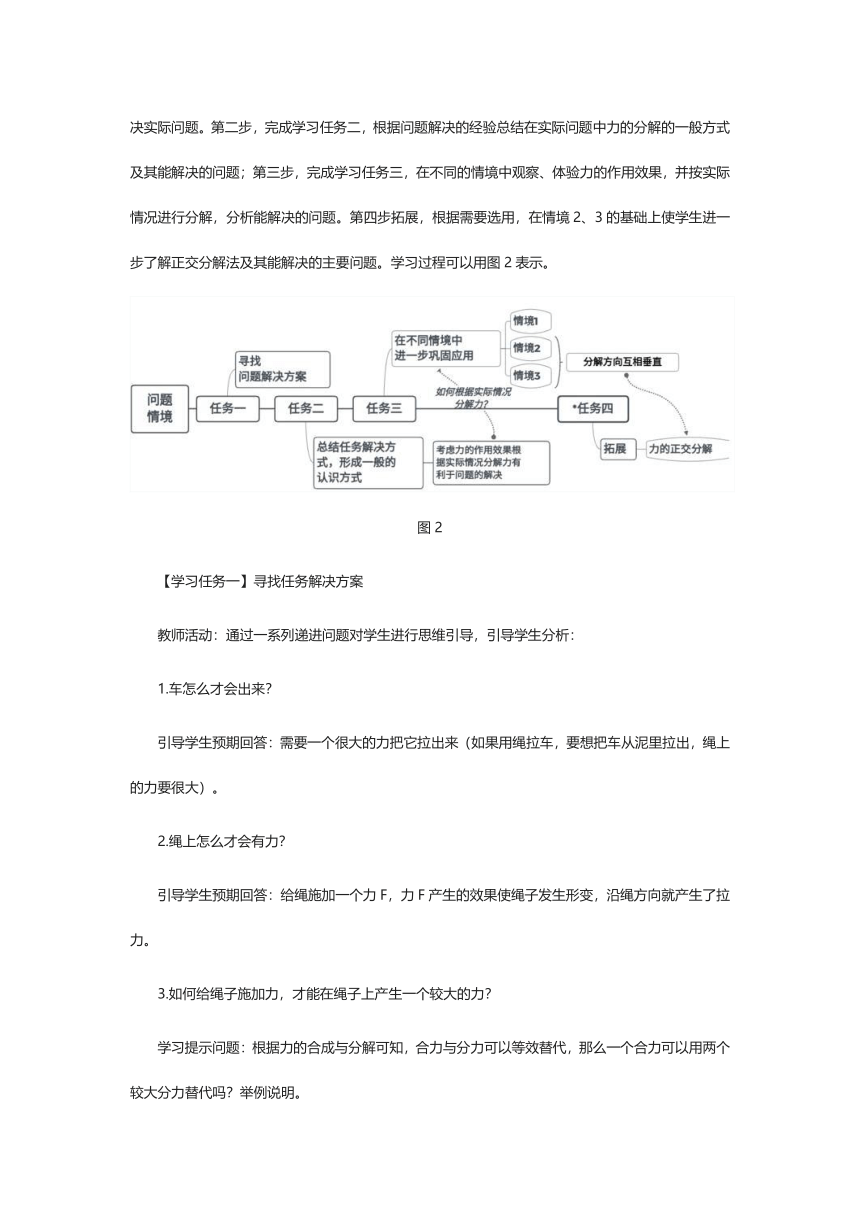
采用归纳演绎的方式,在任务情境分析解决的基础上,总结在实际问题中力的分解的一般方法,再在不同情境中进行学习巩固,并进一步拓展。第一步,完成学习任务一,通过对学生思维的引导,在任务情境中使学生学习体会问题解决的思维过程,形成解决问题的能力,并学习使用力的分解来解决实际问题。第二步,完成学习任务二,根据问题解决的经验总结在实际问题中力的分解的一般方式及其能解决的问题;第三步,完成学习任务三,在不同的情境中观察、体验力的作用效果,并按实际情况进行分解,分析能解决的问题。第四步拓展,根据需要选用,在情境2、3的基础上使学生进一步了解正交分解法及其能解决的主要问题。学习过程可以用图2表示。
图2
【学习任务一】寻找任务解决方案
教师活动:通过一系列递进问题对学生进行思维引导,引导学生分析:
1.车怎么才会出来?
引导学生预期回答:需要一个很大的力把它拉出来(如果用绳拉车,要想把车从泥里拉出,绳上的力要很大)。
2.绳上怎么才会有力?
引导学生预期回答:给绳施加一个力F,力F产生的效果使绳子发生形变,沿绳方向就产生了拉力。
3.如何给绳子施加力,才能在绳子上产生一个较大的力?
学习提示问题:根据力的合成与分解可知,合力与分力可以等效替代,那么一个合力可以用两个较大分力替代吗?举例说明。
回答:如图3所示,由平行四边形定则可知一个力可以用两个较大的分力替代,且两个分力的夹角越大则分力越大。
讨论问题解决方案。
引导学生预期回答:用绳子把大树和汽车连接起来,在绳子中间垂直于绳子的方向施加拉力F,此时两段绳子会形成很大的夹角,由平行四边形定则可知沿绳子的分力会很大。即用一个较小的力F垂直拉绳子等效于沿绳子方向施加很大的两个力,使绳子发生了很大的形变,产生了弹力且根据平衡弹力与分力相等,弹力(分力)足够大就可以把车从泥里拉出来了,如图4、图5所示。
【学习任务二】对上述任务解决方案进行分析,总结在实际问题中力的分解的一般方式及能解决的问题。
教师:组织学生交流和讨论。
提示问题:我们是沿什么方向分解的力?为什么这么分?解决了什么问题?
预期回答:我们是沿绳的方向分解的力,因为由于施加力 F使绳子发生了形变,在绳上产生了弹力,绳上的弹力与分力大小相等。通过求解分力,能知道绳上弹力的大小。
结论:从这个问题的解决可以看出,在实际问题中我们可以根据力的作用效果考虑分解力的方式,这样可以方便找到力的作用关系,有利于问题的解决。
【学习任务三】在不同情境的实际问题中观察、体验力的作用效果,并按实际情况分解力;分析能解决的问题。
教师活动:创设体验情境,引导学生分析体验力的作用效果,并引导学生进行分解。
体验情境1
如图6所示体验在O点挂上重物之后产生了什么效果?按实际情况可以如何分解重物对O点的拉力F,能解决什么问题?
学生通过自己操作如图6所示的实验体验力F的作用效果,并进行分解:
力的分解如图7所示:F1= F/ sinθ F2= F/tanθ
分析解决的问题:由力的分解和装置所处的状态可知:
(1)绳子中的弹力T=F1= F/ sinθ (2)杆中的弹力N= F2= F /tanθ
体验情境2
如图8所示的实验,放在斜面上的物体所受的重力G产生了什么作用效果?按实际情况可以如何分解重力G?能解决什么问题?
学生通过如图8所示的演示实验体验力的作用效果,并进行分解:
力的分解如图9所示:根据效果可分解为平行于斜面的分量F1和垂直于斜面的分量F2。F1使物体下滑(故有时称为“下滑力”),F1= G sinθ (下滑力);F2使物体压紧斜面F2= G cosθ
分析解决的问题:
由力的分解和装置所处的状态可知:
(1)斜面与物体之间的挤压力N= F2= G cosθ
(2)如果物体静止,如图9所示斜面与物体之间的摩擦力(或如图8所示挡板给物体的作用力)F=F1= G sinθ
体验情境3:
在水平面上有一个重物,用与水平方向成θ角的力斜向上拉,但没拉动,物体仍保持静止,拉力F产生了什么效果,按实际情况可以如何分解力F?能解决什么问题?
学生通过分析力F的作用效果,对力F进行分解:
力的分解如图10所示:F1= F cosθ F2 = F sinθ
分析解决的问题:
由力的分解和物体所处的状态可知:
(1)物体保持静止则地面给物体的摩擦力f = F1 = F cosθ
(2)地面与物体之间的挤压力N=G - F2 = G-F sinθ
学生分组实验验证:如图11所示在台秤上放一重物,观察示数,用一力F(可用弹簧测力计施加)斜向上某一角度拉物体观察台秤示数变化,进一步体会和验证力F的作用效果。
【学习任务四】拓展学习:力的正交分解
教师讲授:在情境2、3中两个分力的方向互相垂直,这样的分解我们又叫力的正交分解。如图12所示。
如图12所示,将力F沿力x、y方向分解,可得:
当物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,然后求两个方向上的力的合力∑Fx、∑Fy,这样可把复杂问题简化,尤其是在求多个力的合力时,用正交分解的方法,先将力分解再用勾股定理把∑Fx、∑Fy进行合成,是一种很好的求合力的方法。
注意:坐标的选取原则上是任意的,实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力。
【学习小结】
教师:组织学生总结并表述本部分所学的主要内容。
【学习评价自测】
1.为什么斧刃夹角越小越锋利,越容易劈开木材?
解析:如图13所示斧刃夹角越小,能够替代合力的两个分力的夹角越大,则两个分力越大,作用在侧向木头上的压力越大,就越锋利越容易劈开木材,如图14所示。
2.如图15所示,重为G的物体放在倾角为θ的光滑斜面上,分别被垂直于斜面的挡板(如甲图)和竖直放置的挡板(如乙图)挡住。试对两个图中物体所受的重力根据力的作用效果进行分解,画出示意图,并求出两分力的大小。
解析:如图16所示:
课前准备:回忆之前学过的力的合成与分解的基本知识
1.什么是合力、分力?合力与分力有什么关系?
2.什么是力的合成?力的分解?
3.力的合成与分解遵循什么法则?
4.一个力可以有多少种分解方法?如何确定唯一的解?
课堂教学:
【任务情景】
小明独自驾车陷入淤泥,路旁有很多大树(如图1所示),后备箱中只有一根足够长的粗绳,你能给他出个主意拉出汽车吗?
【教学策略】
采用归纳演绎的方式,在任务情境分析解决的基础上,总结在实际问题中力的分解的一般方法,再在不同情境中进行学习巩固,并进一步拓展。第一步,完成学习任务一,通过对学生思维的引导,在任务情境中使学生学习体会问题解决的思维过程,形成解决问题的能力,并学习使用力的分解来解决实际问题。第二步,完成学习任务二,根据问题解决的经验总结在实际问题中力的分解的一般方式及其能解决的问题;第三步,完成学习任务三,在不同的情境中观察、体验力的作用效果,并按实际情况进行分解,分析能解决的问题。第四步拓展,根据需要选用,在情境2、3的基础上使学生进一步了解正交分解法及其能解决的主要问题。学习过程可以用图2表示。
图2
【学习任务一】寻找任务解决方案
教师活动:通过一系列递进问题对学生进行思维引导,引导学生分析:
1.车怎么才会出来?
引导学生预期回答:需要一个很大的力把它拉出来(如果用绳拉车,要想把车从泥里拉出,绳上的力要很大)。
2.绳上怎么才会有力?
引导学生预期回答:给绳施加一个力F,力F产生的效果使绳子发生形变,沿绳方向就产生了拉力。
3.如何给绳子施加力,才能在绳子上产生一个较大的力?
学习提示问题:根据力的合成与分解可知,合力与分力可以等效替代,那么一个合力可以用两个较大分力替代吗?举例说明。
回答:如图3所示,由平行四边形定则可知一个力可以用两个较大的分力替代,且两个分力的夹角越大则分力越大。
讨论问题解决方案。
引导学生预期回答:用绳子把大树和汽车连接起来,在绳子中间垂直于绳子的方向施加拉力F,此时两段绳子会形成很大的夹角,由平行四边形定则可知沿绳子的分力会很大。即用一个较小的力F垂直拉绳子等效于沿绳子方向施加很大的两个力,使绳子发生了很大的形变,产生了弹力且根据平衡弹力与分力相等,弹力(分力)足够大就可以把车从泥里拉出来了,如图4、图5所示。
【学习任务二】对上述任务解决方案进行分析,总结在实际问题中力的分解的一般方式及能解决的问题。
教师:组织学生交流和讨论。
提示问题:我们是沿什么方向分解的力?为什么这么分?解决了什么问题?
预期回答:我们是沿绳的方向分解的力,因为由于施加力 F使绳子发生了形变,在绳上产生了弹力,绳上的弹力与分力大小相等。通过求解分力,能知道绳上弹力的大小。
结论:从这个问题的解决可以看出,在实际问题中我们可以根据力的作用效果考虑分解力的方式,这样可以方便找到力的作用关系,有利于问题的解决。
【学习任务三】在不同情境的实际问题中观察、体验力的作用效果,并按实际情况分解力;分析能解决的问题。
教师活动:创设体验情境,引导学生分析体验力的作用效果,并引导学生进行分解。
体验情境1
如图6所示体验在O点挂上重物之后产生了什么效果?按实际情况可以如何分解重物对O点的拉力F,能解决什么问题?
学生通过自己操作如图6所示的实验体验力F的作用效果,并进行分解:
力的分解如图7所示:F1= F/ sinθ F2= F/tanθ
分析解决的问题:由力的分解和装置所处的状态可知:
(1)绳子中的弹力T=F1= F/ sinθ (2)杆中的弹力N= F2= F /tanθ
体验情境2
如图8所示的实验,放在斜面上的物体所受的重力G产生了什么作用效果?按实际情况可以如何分解重力G?能解决什么问题?
学生通过如图8所示的演示实验体验力的作用效果,并进行分解:
力的分解如图9所示:根据效果可分解为平行于斜面的分量F1和垂直于斜面的分量F2。F1使物体下滑(故有时称为“下滑力”),F1= G sinθ (下滑力);F2使物体压紧斜面F2= G cosθ
分析解决的问题:
由力的分解和装置所处的状态可知:
(1)斜面与物体之间的挤压力N= F2= G cosθ
(2)如果物体静止,如图9所示斜面与物体之间的摩擦力(或如图8所示挡板给物体的作用力)F=F1= G sinθ
体验情境3:
在水平面上有一个重物,用与水平方向成θ角的力斜向上拉,但没拉动,物体仍保持静止,拉力F产生了什么效果,按实际情况可以如何分解力F?能解决什么问题?
学生通过分析力F的作用效果,对力F进行分解:
力的分解如图10所示:F1= F cosθ F2 = F sinθ
分析解决的问题:
由力的分解和物体所处的状态可知:
(1)物体保持静止则地面给物体的摩擦力f = F1 = F cosθ
(2)地面与物体之间的挤压力N=G - F2 = G-F sinθ
学生分组实验验证:如图11所示在台秤上放一重物,观察示数,用一力F(可用弹簧测力计施加)斜向上某一角度拉物体观察台秤示数变化,进一步体会和验证力F的作用效果。
【学习任务四】拓展学习:力的正交分解
教师讲授:在情境2、3中两个分力的方向互相垂直,这样的分解我们又叫力的正交分解。如图12所示。
如图12所示,将力F沿力x、y方向分解,可得:
当物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,然后求两个方向上的力的合力∑Fx、∑Fy,这样可把复杂问题简化,尤其是在求多个力的合力时,用正交分解的方法,先将力分解再用勾股定理把∑Fx、∑Fy进行合成,是一种很好的求合力的方法。
注意:坐标的选取原则上是任意的,实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力。
【学习小结】
教师:组织学生总结并表述本部分所学的主要内容。
【学习评价自测】
1.为什么斧刃夹角越小越锋利,越容易劈开木材?
解析:如图13所示斧刃夹角越小,能够替代合力的两个分力的夹角越大,则两个分力越大,作用在侧向木头上的压力越大,就越锋利越容易劈开木材,如图14所示。
2.如图15所示,重为G的物体放在倾角为θ的光滑斜面上,分别被垂直于斜面的挡板(如甲图)和竖直放置的挡板(如乙图)挡住。试对两个图中物体所受的重力根据力的作用效果进行分解,画出示意图,并求出两分力的大小。
解析:如图16所示:
