第八章《机械能守恒定律》学习活动设计五:怎样理解机械能守恒定律?(word教案)
文档属性
| 名称 | 第八章《机械能守恒定律》学习活动设计五:怎样理解机械能守恒定律?(word教案) |  | |
| 格式 | zip | ||
| 文件大小 | 296.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-10 13:18:55 | ||
图片预览



文档简介
第八章《机械能守恒定律》学习活动设计五:怎样理解机械能守恒定律?
【任务情境】
演示实验:伽利略曾研究过的小球在斜面上运动的实验。
通过实验现象发现:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度h与它出发时的高度h基本相同(如图1)。
想一想在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
图1
【学习任务一】追寻守恒量
提问:请同学们利用力和运动的关系,解释伽利略斜面实验的现象?
学生:小球在力的作用下加速滚下斜面A,到达斜面的底部,由于惯性而滚上斜面B。
教师:伽利略实验中,小球好像“记住”了原来的高度。利用以前的知识来描述,不能直接表达一个最重要的事实:如果空气阻力和摩擦力小到可以忽略,小球必将准确地终止于它开始运动时的高度,不会更高一点,也不会更低一点。
提问:伽利略年代没有“能量”的概念,当时的描述不能直接表达某种“东西”是不变的,接下来请同学们再用能量的观点,解释实验的现象?
学生:小球滚下斜面A过程,重力势能转化为动能。滚上斜面B过程,小球动能转化为重力势能。如果空气阻力和摩擦力小到可以忽略,小球必将准确地达到开始运动时的高度。
教师:这个解释,说明在小球运动的过程中某种量—能量是不变的。能量概念的引入是科学前辈们追寻守恒量的一个重要事例。能量及其转化将各种运动统一、联系起来。
【学习任务二】动能和势能的相互转化
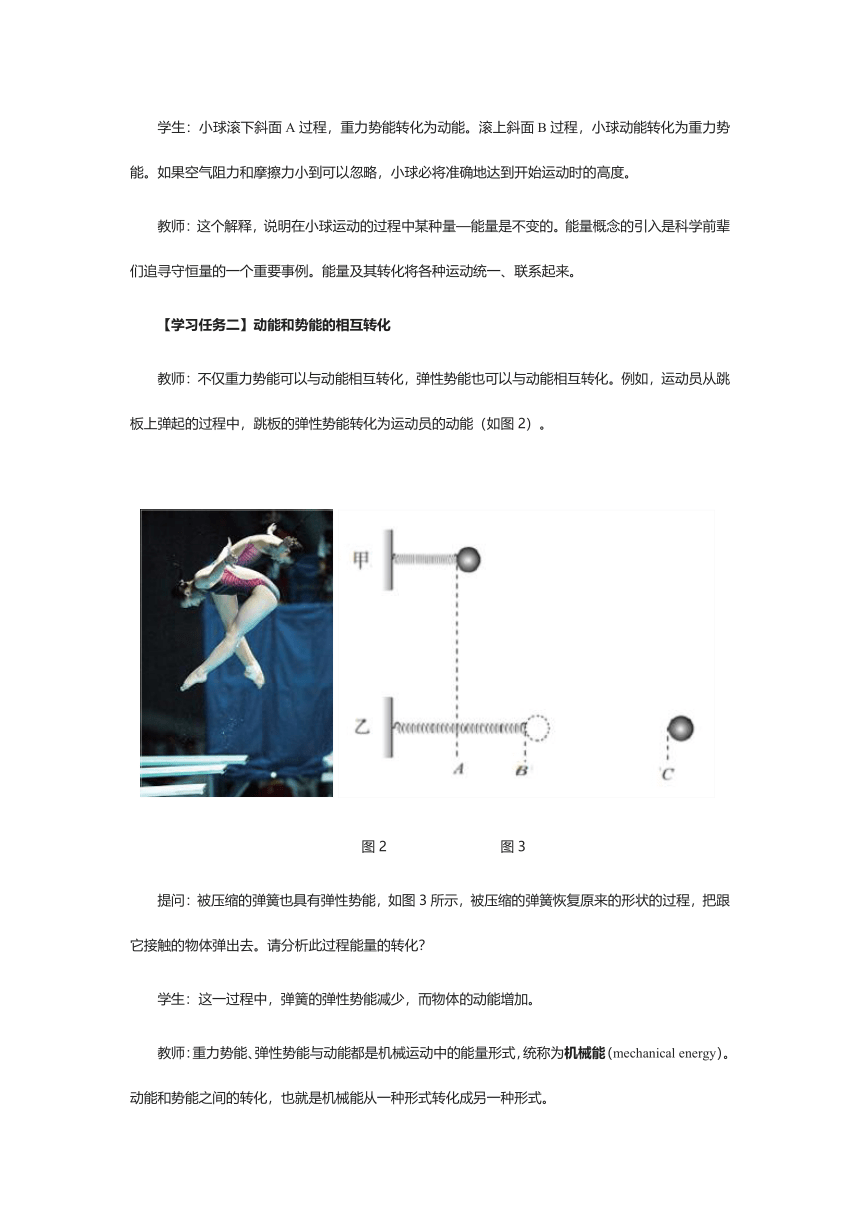
教师:不仅重力势能可以与动能相互转化,弹性势能也可以与动能相互转化。例如,运动员从跳板上弹起的过程中,跳板的弹性势能转化为运动员的动能(如图2)。
图2 图3
提问:被压缩的弹簧也具有弹性势能,如图3所示,被压缩的弹簧恢复原来的形状的过程,把跟它接触的物体弹出去。请分析此过程能量的转化?
学生:这一过程中,弹簧的弹性势能减少,而物体的动能增加。
教师:重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能(mechanical energy)。动能和势能之间的转化,也就是机械能从一种形式转化成另一种形式。
提问:动能和重力势能转化的过程是什么力做功?
学生:重力做功。
教师:动能和弹性势能转化的过程是什么力做功?
学生:弹力做功。
教师追问:同学们可以归纳出机械能转化的过程是什么力做功吗?
学生:重力做功或弹力做功。
教师:如果除了重力与弹力做功外,有其他力做功,能量会有怎样变化,接下来一起做一个对比分析。
问题情境:如图4所示,同样的小球在两种情况下,下落同样的高度。
提问1:重力做的功相等吗?重力势能的变化相等吗?
小球在真空和油中均从同一高度由静止开始下落到相同的另一高度
图4
学生:重力做的功相等。重力势能的变化也相等。
提问2:动能的变化相等吗?两种情况下,重力势能分别转化成什么形式的能?
学生:动能的变化不相等。小球在真空中下落,减少的重力势能全部转化成动能;小球在油中下落,减少的重力势能一部分转化成动能,另一部分转化成内能。
教师:小球在真空中下落,只有重力做功,重力势能全部转化为动能。
【学习任务三】机械能守恒定律
教师:接下来分析动能与势能转化的定量关系。先来分析动能与重力势能相互转化的问题。
学习活动1:物体沿光滑曲面滑下的情境
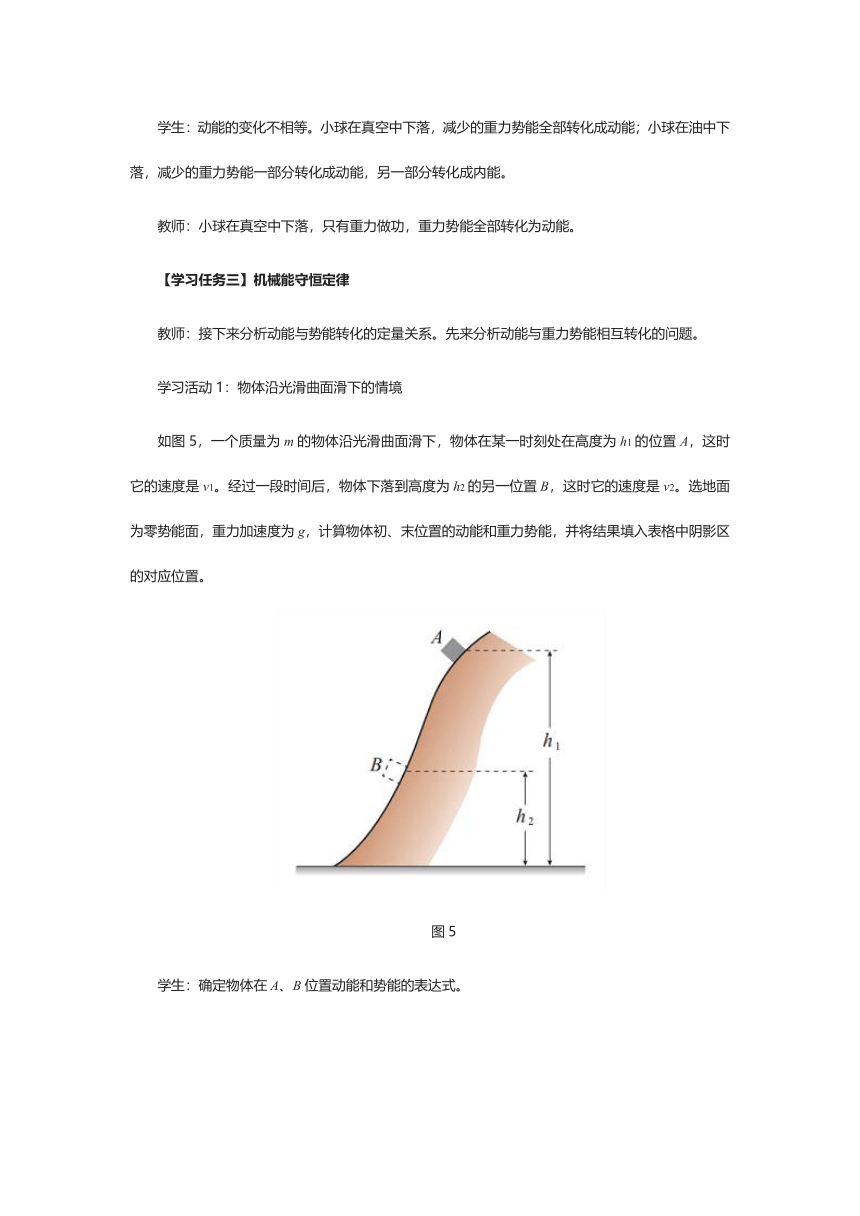
如图5,一个质量为m的物体沿光滑曲面滑下,物体在某一时刻处在高度为h1的位置A,这时它的速度是v1。经过一段时间后,物体下落到高度为h2的另一位置B,这时它的速度是v2。选地面为零势能面,重力加速度为g,计算物体初、末位置的动能和重力势能,并将结果填入表格中阴影区的对应位置。
图5
学生:确定物体在A、B位置动能和势能的表达式。
教师:请分别写出这一过程动能定理的表达式及重力做功与重力势能变化的表达式。
学生活动:写出表达式
①
②
教师:①②两式联立已经可以说明动能与重力势能转化的定量关系了,你能发现这个定量关系吗?
学生:物体受到重力和曲面支持力的作用,支持力方向与运动方向垂直,不做功。这一过程中,只有重力做功,两式中的功是相同的,即。
教师:两式联立计算可得
③
请思考讨论如何理解关系式③?
学生:只有重力做功时,有多少重力势能减少就有多少动能的增加。
教师:把上式移项后得到
④
请思考讨论如何理解关系式④?
学生:只有重力做功时,物体在位置A的动能与重力势能之和,等于物体在位置B的动能与重力势能之和。
教师:也就是说,在只有重力做功时,动能与重力势能互相转化,而总的机械能保持不变。
学习活动2:物体沿光滑曲面上升的情境
在图5中,如果物体从位置B沿光滑曲面上升到位置A,重力做负功。这种情况下③式和④式的关系是否还成立?请小组讨论并证明你的观点(设物体在位置A、B时的动能分别为、)。
学生:虽然重力对物体做的功是负功,关系式依然成立,计算过程为:
位置B→A过程动能的变化:
位置B→A过程重力势能的变化:
教师:只有重力做功,动能和重力势能互相转化,而总的机械能保持不变。同样可以证明,只有弹力做功,动能和弹性势能互相转化时总的机械能也保持不变。
提问:根据上面的分析,你能归纳出怎样的结论?
学生:只有重力或弹力做功,势能的增加(减少)等于动能的减少(增加),机械能保持不变。
教师:通过同学们的归纳整理,可以证明:在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变。这叫作机械能守恒定律(law of conservation of mechanical energy)。
机械能守恒定律是力学中的一条重要定律,是普遍的能量守恒定律在力学范围内的表现形式。严格说来,势能是物体与地球组成的“系统”所共有的,而不是某个物体单独具有的。
【例题1】
滑雪者沿斜面下滑时(如图6),如果阻力做的功较少,可以忽略,机械能是否守恒?说明理由。
图6
学生:机械能守恒。因为只有重力做功,动能与重力势能相互转化,总的机械能守恒。
教师:如果阻力做的功较大,不能忽略,则机械能就不守恒了。例如,滑雪者匀速下滑,动能不变重力势能减小,总机械能减小。
【例题2】
把一个小球用细线悬挂起来,就成为一个摆(如图7),摆长为l,最大偏角为θ。如果阻力可以忽略,小球运动到最低点时的速度大小是多少?
图7
教师:要计算小球在最低点时的速度大小,应该思考几个问题。
(1)小球摆动过程中受哪几个力作用?
(2)小球摆动过程中什么力做功?
(3)这个过程中机械能守恒吗?
学生:
(1)小球受重力和细线的拉力作用。
(2)因为细线的拉力与小球的运动方向垂直,不做功,所以只有重力做功。
(3)这个过程中机械能守恒。
解:以小球为研究对象,小球在最高点只有重力势能,动能为0。为了方便计算,设最低点的重力势能为0。
在最高点的动能Ek1=0,重力势能是Ep1=mg(l-lcosθ)
在最低点的重力势能Ep2=0,而动能可以表示为Ek2=
运动过程中只有重力做功,所以机械能守恒,即
Ek2+Ep2=Ek1+Ep1
把初、末状态下动能、重力势能的表达式代入,得
=mg(l-lcosθ)
由此解出小球运动到最低点时的速度大小
v=
教师:从得到的表达式可以看出,初状态的θ角越大,cosθ越小,(1-cosθ)就越大,v也就越大。也就是说,最初把小球拉得越高,它到达最低点时的速度也就越大。这与生活经验是一致的。
从这个例题可以看出,如果研究对象在某一过程中满足机械能守恒的条件,应用机械能守恒定律解决问题只需考虑运动的初状态和末状态,不必考虑两个状态间所经历过程的细节。
【学习小结】
1.人们发现有些物理量在一定条件下是守恒的,可以用这些“守恒量”来表示物理世界变化的规律,这就是守恒定律。机械能守恒定律就是其中之一。
2.重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
3.在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变。这叫做机械能守恒定律。它是力学中的一条重要定律,是普遍的能量守恒定律在力学范围内的表现形式。
【学习评价自测】
1.在下面列举的各个实例中(除A外都不计空气阻力),哪些过程中机械能是守恒的?说明理由。
A.跳伞运动员带着张开的降落伞在空气中匀速下落
B.被抛出的标枪在空中运动
C.拉着一个金属块使它沿光滑的斜面匀速上升
D.在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来
答案:A.跳伞运动员带着张开的降落伞在空气中匀速下落时,动能不变,重力势能减小,机械能减小,不守恒;
B.被抛出的标枪在空中飞行时只有重力做功,机械能守恒;
C.金属块在拉力作用下沿着光滑的斜面匀速上升时,动能不变,势能变大,故机械能变大,不守恒;
D.小球碰到弹簧被弹回的过程中只有弹簧弹力做功,机械能守恒。
故选项B、D机械能守恒。
2.把质量是0.2kg的小球放在竖立的弹簧上,并把球往下按至A的位置(图甲所示),迅速松手,弹簧把球弹起,球升至最高位置C(图丙所示),途中经过位置B时弹簧正好处于自由状态(图乙所示)。已知B、A高度差为0.1m,C、B的高度差为0.2m,弹簧的质量和空气的阻力均不计,g取10m/s2。
(1)状态甲中弹簧的弹性势能是多少?
(2)状态乙中小球的动能是多少?
答案:(1)0.6 J (2)0.4 J
【任务情境】
演示实验:伽利略曾研究过的小球在斜面上运动的实验。
通过实验现象发现:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度h与它出发时的高度h基本相同(如图1)。
想一想在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
图1
【学习任务一】追寻守恒量
提问:请同学们利用力和运动的关系,解释伽利略斜面实验的现象?
学生:小球在力的作用下加速滚下斜面A,到达斜面的底部,由于惯性而滚上斜面B。
教师:伽利略实验中,小球好像“记住”了原来的高度。利用以前的知识来描述,不能直接表达一个最重要的事实:如果空气阻力和摩擦力小到可以忽略,小球必将准确地终止于它开始运动时的高度,不会更高一点,也不会更低一点。
提问:伽利略年代没有“能量”的概念,当时的描述不能直接表达某种“东西”是不变的,接下来请同学们再用能量的观点,解释实验的现象?
学生:小球滚下斜面A过程,重力势能转化为动能。滚上斜面B过程,小球动能转化为重力势能。如果空气阻力和摩擦力小到可以忽略,小球必将准确地达到开始运动时的高度。
教师:这个解释,说明在小球运动的过程中某种量—能量是不变的。能量概念的引入是科学前辈们追寻守恒量的一个重要事例。能量及其转化将各种运动统一、联系起来。
【学习任务二】动能和势能的相互转化
教师:不仅重力势能可以与动能相互转化,弹性势能也可以与动能相互转化。例如,运动员从跳板上弹起的过程中,跳板的弹性势能转化为运动员的动能(如图2)。
图2 图3
提问:被压缩的弹簧也具有弹性势能,如图3所示,被压缩的弹簧恢复原来的形状的过程,把跟它接触的物体弹出去。请分析此过程能量的转化?
学生:这一过程中,弹簧的弹性势能减少,而物体的动能增加。
教师:重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能(mechanical energy)。动能和势能之间的转化,也就是机械能从一种形式转化成另一种形式。
提问:动能和重力势能转化的过程是什么力做功?
学生:重力做功。
教师:动能和弹性势能转化的过程是什么力做功?
学生:弹力做功。
教师追问:同学们可以归纳出机械能转化的过程是什么力做功吗?
学生:重力做功或弹力做功。
教师:如果除了重力与弹力做功外,有其他力做功,能量会有怎样变化,接下来一起做一个对比分析。
问题情境:如图4所示,同样的小球在两种情况下,下落同样的高度。
提问1:重力做的功相等吗?重力势能的变化相等吗?
小球在真空和油中均从同一高度由静止开始下落到相同的另一高度
图4
学生:重力做的功相等。重力势能的变化也相等。
提问2:动能的变化相等吗?两种情况下,重力势能分别转化成什么形式的能?
学生:动能的变化不相等。小球在真空中下落,减少的重力势能全部转化成动能;小球在油中下落,减少的重力势能一部分转化成动能,另一部分转化成内能。
教师:小球在真空中下落,只有重力做功,重力势能全部转化为动能。
【学习任务三】机械能守恒定律
教师:接下来分析动能与势能转化的定量关系。先来分析动能与重力势能相互转化的问题。
学习活动1:物体沿光滑曲面滑下的情境
如图5,一个质量为m的物体沿光滑曲面滑下,物体在某一时刻处在高度为h1的位置A,这时它的速度是v1。经过一段时间后,物体下落到高度为h2的另一位置B,这时它的速度是v2。选地面为零势能面,重力加速度为g,计算物体初、末位置的动能和重力势能,并将结果填入表格中阴影区的对应位置。
图5
学生:确定物体在A、B位置动能和势能的表达式。
教师:请分别写出这一过程动能定理的表达式及重力做功与重力势能变化的表达式。
学生活动:写出表达式
①
②
教师:①②两式联立已经可以说明动能与重力势能转化的定量关系了,你能发现这个定量关系吗?
学生:物体受到重力和曲面支持力的作用,支持力方向与运动方向垂直,不做功。这一过程中,只有重力做功,两式中的功是相同的,即。
教师:两式联立计算可得
③
请思考讨论如何理解关系式③?
学生:只有重力做功时,有多少重力势能减少就有多少动能的增加。
教师:把上式移项后得到
④
请思考讨论如何理解关系式④?
学生:只有重力做功时,物体在位置A的动能与重力势能之和,等于物体在位置B的动能与重力势能之和。
教师:也就是说,在只有重力做功时,动能与重力势能互相转化,而总的机械能保持不变。
学习活动2:物体沿光滑曲面上升的情境
在图5中,如果物体从位置B沿光滑曲面上升到位置A,重力做负功。这种情况下③式和④式的关系是否还成立?请小组讨论并证明你的观点(设物体在位置A、B时的动能分别为、)。
学生:虽然重力对物体做的功是负功,关系式依然成立,计算过程为:
位置B→A过程动能的变化:
位置B→A过程重力势能的变化:
教师:只有重力做功,动能和重力势能互相转化,而总的机械能保持不变。同样可以证明,只有弹力做功,动能和弹性势能互相转化时总的机械能也保持不变。
提问:根据上面的分析,你能归纳出怎样的结论?
学生:只有重力或弹力做功,势能的增加(减少)等于动能的减少(增加),机械能保持不变。
教师:通过同学们的归纳整理,可以证明:在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变。这叫作机械能守恒定律(law of conservation of mechanical energy)。
机械能守恒定律是力学中的一条重要定律,是普遍的能量守恒定律在力学范围内的表现形式。严格说来,势能是物体与地球组成的“系统”所共有的,而不是某个物体单独具有的。
【例题1】
滑雪者沿斜面下滑时(如图6),如果阻力做的功较少,可以忽略,机械能是否守恒?说明理由。
图6
学生:机械能守恒。因为只有重力做功,动能与重力势能相互转化,总的机械能守恒。
教师:如果阻力做的功较大,不能忽略,则机械能就不守恒了。例如,滑雪者匀速下滑,动能不变重力势能减小,总机械能减小。
【例题2】
把一个小球用细线悬挂起来,就成为一个摆(如图7),摆长为l,最大偏角为θ。如果阻力可以忽略,小球运动到最低点时的速度大小是多少?
图7
教师:要计算小球在最低点时的速度大小,应该思考几个问题。
(1)小球摆动过程中受哪几个力作用?
(2)小球摆动过程中什么力做功?
(3)这个过程中机械能守恒吗?
学生:
(1)小球受重力和细线的拉力作用。
(2)因为细线的拉力与小球的运动方向垂直,不做功,所以只有重力做功。
(3)这个过程中机械能守恒。
解:以小球为研究对象,小球在最高点只有重力势能,动能为0。为了方便计算,设最低点的重力势能为0。
在最高点的动能Ek1=0,重力势能是Ep1=mg(l-lcosθ)
在最低点的重力势能Ep2=0,而动能可以表示为Ek2=
运动过程中只有重力做功,所以机械能守恒,即
Ek2+Ep2=Ek1+Ep1
把初、末状态下动能、重力势能的表达式代入,得
=mg(l-lcosθ)
由此解出小球运动到最低点时的速度大小
v=
教师:从得到的表达式可以看出,初状态的θ角越大,cosθ越小,(1-cosθ)就越大,v也就越大。也就是说,最初把小球拉得越高,它到达最低点时的速度也就越大。这与生活经验是一致的。
从这个例题可以看出,如果研究对象在某一过程中满足机械能守恒的条件,应用机械能守恒定律解决问题只需考虑运动的初状态和末状态,不必考虑两个状态间所经历过程的细节。
【学习小结】
1.人们发现有些物理量在一定条件下是守恒的,可以用这些“守恒量”来表示物理世界变化的规律,这就是守恒定律。机械能守恒定律就是其中之一。
2.重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
3.在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变。这叫做机械能守恒定律。它是力学中的一条重要定律,是普遍的能量守恒定律在力学范围内的表现形式。
【学习评价自测】
1.在下面列举的各个实例中(除A外都不计空气阻力),哪些过程中机械能是守恒的?说明理由。
A.跳伞运动员带着张开的降落伞在空气中匀速下落
B.被抛出的标枪在空中运动
C.拉着一个金属块使它沿光滑的斜面匀速上升
D.在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来
答案:A.跳伞运动员带着张开的降落伞在空气中匀速下落时,动能不变,重力势能减小,机械能减小,不守恒;
B.被抛出的标枪在空中飞行时只有重力做功,机械能守恒;
C.金属块在拉力作用下沿着光滑的斜面匀速上升时,动能不变,势能变大,故机械能变大,不守恒;
D.小球碰到弹簧被弹回的过程中只有弹簧弹力做功,机械能守恒。
故选项B、D机械能守恒。
2.把质量是0.2kg的小球放在竖立的弹簧上,并把球往下按至A的位置(图甲所示),迅速松手,弹簧把球弹起,球升至最高位置C(图丙所示),途中经过位置B时弹簧正好处于自由状态(图乙所示)。已知B、A高度差为0.1m,C、B的高度差为0.2m,弹簧的质量和空气的阻力均不计,g取10m/s2。
(1)状态甲中弹簧的弹性势能是多少?
(2)状态乙中小球的动能是多少?
答案:(1)0.6 J (2)0.4 J
