圆的方程
图片预览





文档简介
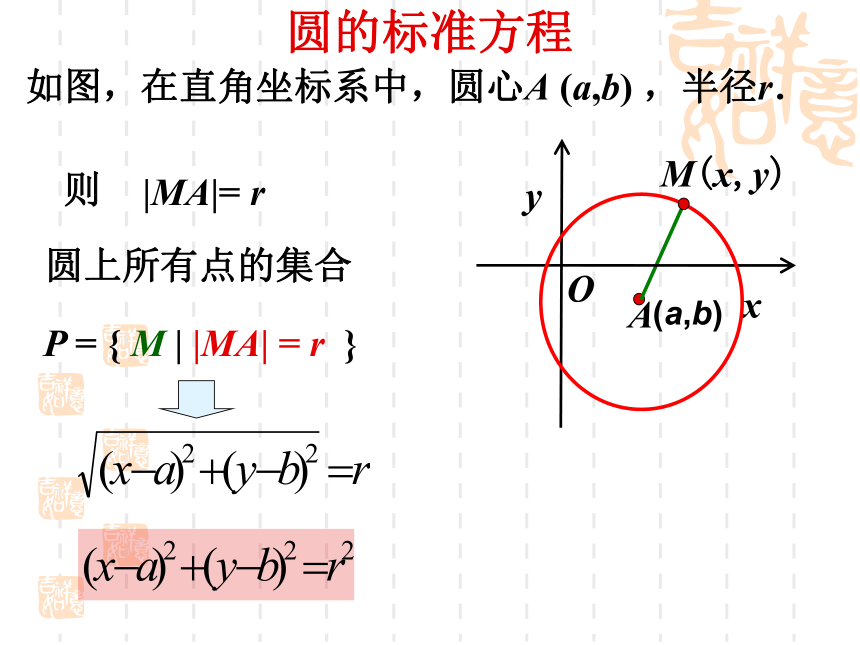
课件15张PPT。4.1.1圆的标准方程4.1.1圆的标准方程圆的定义平面内到定点的距离等于定长的点的集合。定点定长圆心半径因此一个圆最基本的要素是圆心和半径.温故知新思考:在平面直角坐标系中,如何确定一个圆呢?圆的标准方程xy|MA|= r则P = { M | |MA| = r }圆上所有点的集合OAM(x,y) 如图,在直角坐标系中,圆心A (a,b) ,半径r.(a,b) (x-a) 2 + (y-b) 2 = r2称为圆心为A(a,b),半径长为r的圆的标准方程问题:圆的标准方程有什么特征?特别地:圆心在原点,半径为r的圆的方程是什么?(1)有两个变量x,y,形式都是与某个实数差的平方; (2)两个变量的系数都是1 ;(3)方程的右边是某个实数的平方,也就是一定为正数。x2 +y2 = r2圆的标准方程例题讲解例1、写出圆心为 ,半径长等于5的圆的方程,
并判断点 是否在这个圆上.
结论:判断点 与圆
的位置关系:
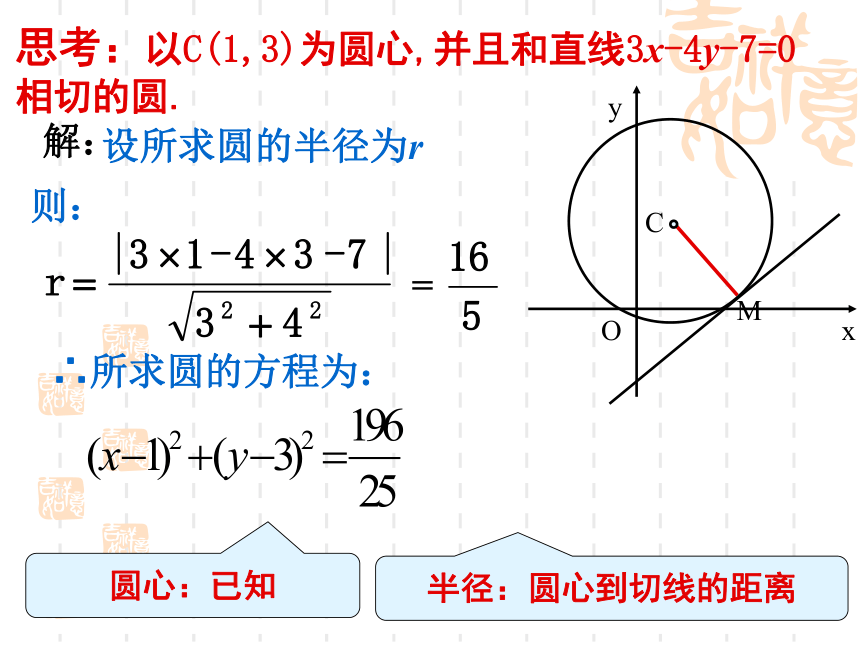
(1)、几何法:点与圆心的距离d与半径r进行比较.(2)、代数法:把点的坐标直接代入圆的标准方程,课本练习1、3思考:以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆.
圆心:已知半径:圆心到切线的距离解:设所求圆的半径为r则:=∴所求圆的方程为:yxOM例2、 的三个顶点的坐标分别A(5,1), B(7,-3), C(2, -8),求它的外接圆的方程.待定系数法(法一)那怎样画这个三角形的外接圆呢?xyOA(5,1)B(7,-3)C(2,-8)例2、 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.法二比较这两种方法,哪一个更为简单?圆心:两条直线的交点半径:圆心到圆上一点xyOA(1,1)B(2,-2)弦AB的垂直平分线例3、已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x -y +1=0,求圆心为C的圆的标准方程. 解:因为A(1, 1)和B(2, -2),所以线段AB的中点D的坐标直线AB的斜率:解方程组得所以圆心C的坐标是圆心为C的圆的半径长所以,圆心为C的圆的标准方程是例3、已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x -y +1=0,求圆心为C的圆的标准方程.解:课本121页练习4练习:解:解:小结圆心C(a,b),半径r1.圆的标准方程2.圆心①弦的垂直平分线的交点②直径的中点3.半径①圆心到圆上一点②圆心到切线的距离求圆的方程方法
1.待定系数法
2.确定圆心,确定半径(利用圆的几何性质)作 业P124 习题4.1 A 3、4
智能提升(23)
预习4.1.2
并判断点 是否在这个圆上.
结论:判断点 与圆
的位置关系:
(1)、几何法:点与圆心的距离d与半径r进行比较.(2)、代数法:把点的坐标直接代入圆的标准方程,课本练习1、3思考:以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆.
圆心:已知半径:圆心到切线的距离解:设所求圆的半径为r则:=∴所求圆的方程为:yxOM例2、 的三个顶点的坐标分别A(5,1), B(7,-3), C(2, -8),求它的外接圆的方程.待定系数法(法一)那怎样画这个三角形的外接圆呢?xyOA(5,1)B(7,-3)C(2,-8)例2、 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.法二比较这两种方法,哪一个更为简单?圆心:两条直线的交点半径:圆心到圆上一点xyOA(1,1)B(2,-2)弦AB的垂直平分线例3、已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x -y +1=0,求圆心为C的圆的标准方程. 解:因为A(1, 1)和B(2, -2),所以线段AB的中点D的坐标直线AB的斜率:解方程组得所以圆心C的坐标是圆心为C的圆的半径长所以,圆心为C的圆的标准方程是例3、已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x -y +1=0,求圆心为C的圆的标准方程.解:课本121页练习4练习:解:解:小结圆心C(a,b),半径r1.圆的标准方程2.圆心①弦的垂直平分线的交点②直径的中点3.半径①圆心到圆上一点②圆心到切线的距离求圆的方程方法
1.待定系数法
2.确定圆心,确定半径(利用圆的几何性质)作 业P124 习题4.1 A 3、4
智能提升(23)
预习4.1.2
