21.3 实际问题与一元二次方程(3) 教案
文档属性
| 名称 | 21.3 实际问题与一元二次方程(3) 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 16:40:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
21.3.1 实际问题与一元二次方程(3) 教案
课题 21.3.1 实际问题与一元二次方程(3) 单元 第21单元 学科 数学 年级 九年级(上)
学习目标 1.能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型.2.能根据具体问题的实际意义,检验结果是否合理.
重点 列一元二次方程解有关特殊图形的应用题.
难点 发现特殊图形问题中的等量关系.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题探究:几何问题如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)? 问题:(1)本题中有哪些数量关系?(2)如何理解“正中央是一个与整个封面长宽比例相同的矩形”?(3)如何利用已知的数量关系选取未知数并列出方程?(4)解方程并得出结论,对比几种方法各有什么特点? 解:依据题意知:中央矩形的长宽之比等于封面的长宽之比=9:7,由此可以判定:上下边衬宽与左右边衬宽之比为9:7,设上、下边衬的宽均为9xcm,则左、右边衬的宽均为7xcm,依题意,得:中央矩形的长为(27-18x)cm,宽为(21-14x)cm. 因为四周的彩色边衬所点面积是封面面积的,则中央矩形的面积是封面面积的. 所以(27-18x)(21-14x)=×27×21 整理,得:16x2-48x+9=0 解方程,得:x= x1≈2.8cm,x2≈0.2 所以:9x1=25.2cm(舍去),9x2=1.8cm,7x2=1.4cm 因此,上下边衬的宽均为1.8cm,左、右边衬的宽均为1.4cm.注意关注学生:(1)对几何图形的分析能力;(2)在未知数的选择上,能否根据情况,灵活处理;(3)在讨论中能否互相合作;(4)解答一元二次方程的能力;(5)回答问题时的语言表达是否准确. 思考自议学生自行探究用其他方法解决问题. 培养学生发散思维能力,用多种方法解决同一问题.
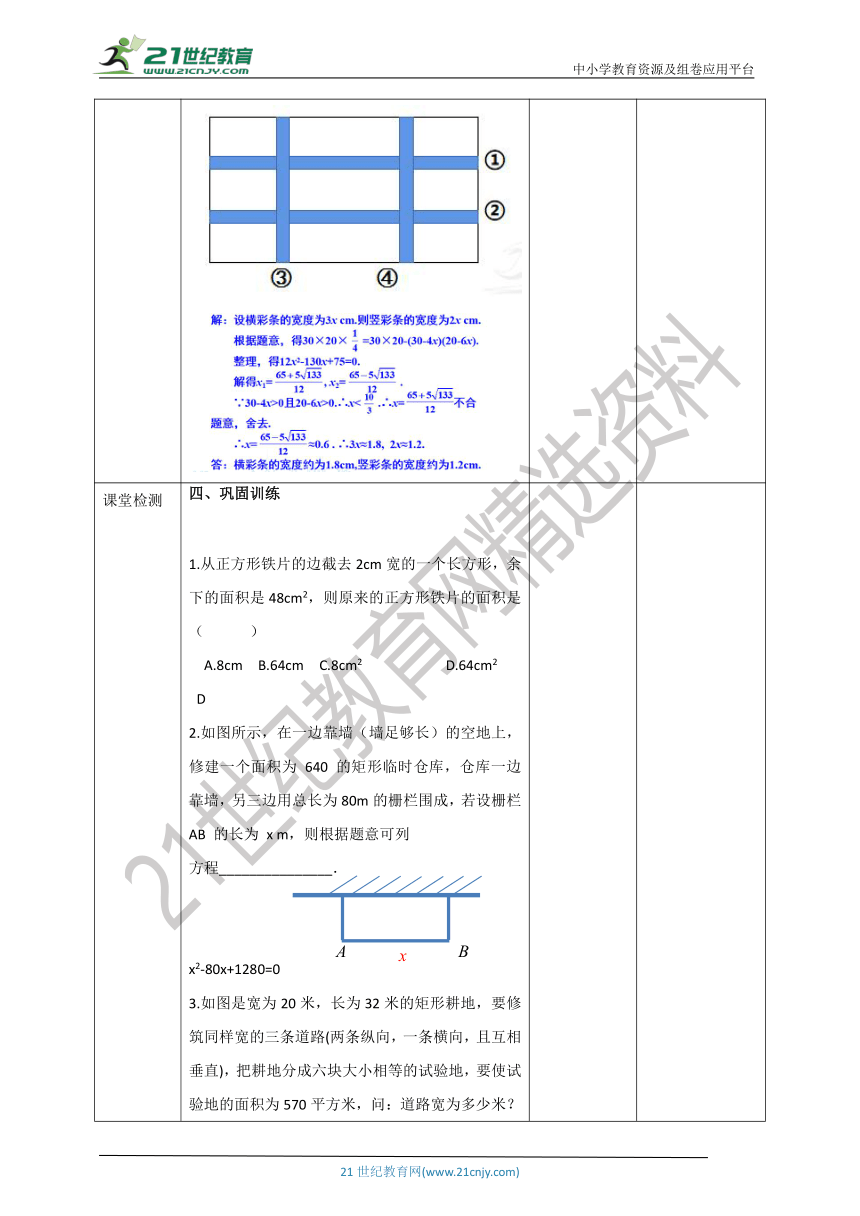
讲授新课 提炼概念小结:几何图形主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程。三、典例精讲例 如图,要设计一幅宽20cm,长30cm的图案,其中有两横、两竖的彩条,横、竖彩条的宽度比为3∶2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)? 师生共同分析,学生发现一元二次方程在实际应用中所要注意的问题. 通过练习,使学生熟练掌握实际问题与一元二次方程的关系.
课堂检测 四、巩固训练 1.从正方形铁片的边截去2cm宽的一个长方形,余下的面积是48cm2,则原来的正方形铁片的面积是( ) A.8cm B.64cm C.8cm2 D.64cm2 D2.如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为 640 的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏 AB 的长为 x m,则根据题意可列方程_______________.x2-80x+1280=03.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?解:设道路宽为x米.由题意知:(32-2x)(20-x)=570解得 x1=1 ,x2=35(舍)答:道路宽为1米.4. 小林准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形. (1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪? (2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.解:(1)设其中一个小正方形的边长为x cm,则另一个小正 方形的边长为 =(10-x)cm. 依题意x2+(10-x)2=58,解得x1=3,x2=7. 当x=3时,小正方形周长为12cm; 当x=7时,小正方形周长为28cm.∴小林应把长为40cm的铁丝剪为28cm和12cm的两段.(2)对.两个正方形的面积之和为: x2+(10-x)2=2x2-20x+100 =2(x2-10x+25)+50=2(x-5)2+50 ∵无论x取何值,2(x-5)2总是不小于0的. ∴2(x-5)2+50≥50.即这两个正方形的面积之和总是不小于50cm2的,所以不可能等于48cm2. 小峰的说法是对的.
课堂小结 通过本节课学习,在几何图形应用题中,我们往往以“面积”来找出等量关系,要灵活地将“面积”拼成一个“整体图形”,使问题更易解决。解决销售问题要很好的利用公式。
A
B
x
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
21.3.1 实际问题与一元二次方程(3) 教案
课题 21.3.1 实际问题与一元二次方程(3) 单元 第21单元 学科 数学 年级 九年级(上)
学习目标 1.能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型.2.能根据具体问题的实际意义,检验结果是否合理.
重点 列一元二次方程解有关特殊图形的应用题.
难点 发现特殊图形问题中的等量关系.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题探究:几何问题如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)? 问题:(1)本题中有哪些数量关系?(2)如何理解“正中央是一个与整个封面长宽比例相同的矩形”?(3)如何利用已知的数量关系选取未知数并列出方程?(4)解方程并得出结论,对比几种方法各有什么特点? 解:依据题意知:中央矩形的长宽之比等于封面的长宽之比=9:7,由此可以判定:上下边衬宽与左右边衬宽之比为9:7,设上、下边衬的宽均为9xcm,则左、右边衬的宽均为7xcm,依题意,得:中央矩形的长为(27-18x)cm,宽为(21-14x)cm. 因为四周的彩色边衬所点面积是封面面积的,则中央矩形的面积是封面面积的. 所以(27-18x)(21-14x)=×27×21 整理,得:16x2-48x+9=0 解方程,得:x= x1≈2.8cm,x2≈0.2 所以:9x1=25.2cm(舍去),9x2=1.8cm,7x2=1.4cm 因此,上下边衬的宽均为1.8cm,左、右边衬的宽均为1.4cm.注意关注学生:(1)对几何图形的分析能力;(2)在未知数的选择上,能否根据情况,灵活处理;(3)在讨论中能否互相合作;(4)解答一元二次方程的能力;(5)回答问题时的语言表达是否准确. 思考自议学生自行探究用其他方法解决问题. 培养学生发散思维能力,用多种方法解决同一问题.
讲授新课 提炼概念小结:几何图形主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程。三、典例精讲例 如图,要设计一幅宽20cm,长30cm的图案,其中有两横、两竖的彩条,横、竖彩条的宽度比为3∶2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)? 师生共同分析,学生发现一元二次方程在实际应用中所要注意的问题. 通过练习,使学生熟练掌握实际问题与一元二次方程的关系.
课堂检测 四、巩固训练 1.从正方形铁片的边截去2cm宽的一个长方形,余下的面积是48cm2,则原来的正方形铁片的面积是( ) A.8cm B.64cm C.8cm2 D.64cm2 D2.如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为 640 的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏 AB 的长为 x m,则根据题意可列方程_______________.x2-80x+1280=03.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?解:设道路宽为x米.由题意知:(32-2x)(20-x)=570解得 x1=1 ,x2=35(舍)答:道路宽为1米.4. 小林准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形. (1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪? (2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.解:(1)设其中一个小正方形的边长为x cm,则另一个小正 方形的边长为 =(10-x)cm. 依题意x2+(10-x)2=58,解得x1=3,x2=7. 当x=3时,小正方形周长为12cm; 当x=7时,小正方形周长为28cm.∴小林应把长为40cm的铁丝剪为28cm和12cm的两段.(2)对.两个正方形的面积之和为: x2+(10-x)2=2x2-20x+100 =2(x2-10x+25)+50=2(x-5)2+50 ∵无论x取何值,2(x-5)2总是不小于0的. ∴2(x-5)2+50≥50.即这两个正方形的面积之和总是不小于50cm2的,所以不可能等于48cm2. 小峰的说法是对的.
课堂小结 通过本节课学习,在几何图形应用题中,我们往往以“面积”来找出等量关系,要灵活地将“面积”拼成一个“整体图形”,使问题更易解决。解决销售问题要很好的利用公式。
A
B
x
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
