21.3实际问题与一元二次方程(3) 课件(共20张PPT)
文档属性
| 名称 | 21.3实际问题与一元二次方程(3) 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 16:44:01 | ||
图片预览








文档简介
(共20张PPT)
21.3.1 实际问题与一元二次方程(3)
人教版九年级上册
教学目标
教学目标:1.能根据实际问题中的数量关系,正确列出一元二次方程;
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
教学重点:列一元二次方程解有关特殊图形的应用题.
教学难点:发现特殊图形问题中的等量关系.
新知导入
情境引入
探究:要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度
(结果保留小数点后一位)
新知讲解
合作学习
分析:封面的长宽之比是
9∶7,中央的矩形的长宽之比也应是 9∶7.
27
21
9a
7a
设中央的矩形的长和宽分别是 9a cm和 7a cm,由此得上、下边衬与左、右边衬的宽度之比是
( )
( )
27 - 9a ∶ 21 - 7a = 9∶7.
整理得:16y 2 - 48y + 9 = 0.
解法一:设上、下边衬的宽均为 9y cm,左、右边
衬宽均为 7y cm,依题意得
方程的哪个根合乎实际意义?为什么?
解方程得
≈1.8 cm,
≈1.4 cm.
( )
( )
27 - 18y 21 - 14y
试一试:如果换一种设未知数的方法,是否可以更简单地解决上面的问题?
解法二:设正中央的矩形两边分别为 9x cm,7x cm,
依题意得
故上、下边衬的宽度为:
解得: , (不合题意,舍去).
左、右边衬的宽度为:
≈1.8 cm,
( )
≈1.4 cm.
( )
提炼概念
几何图形主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程.
典例精讲
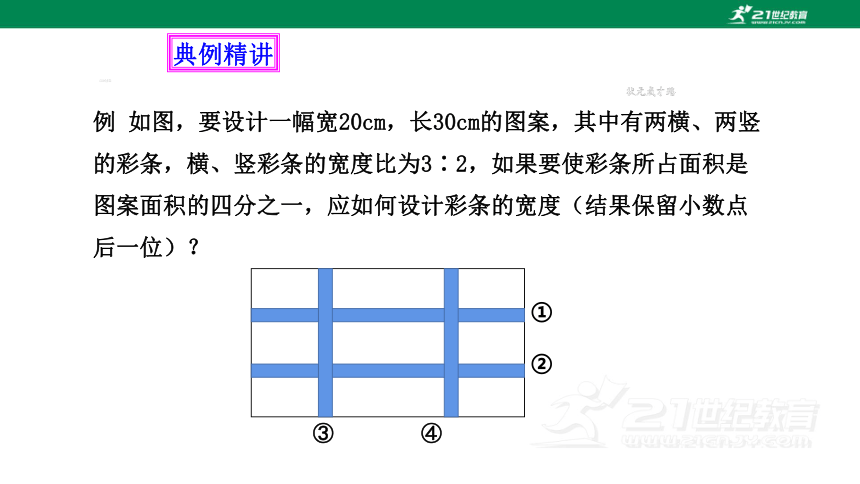
例 如图,要设计一幅宽20cm,长30cm的图案,其中有两横、两竖的彩条,横、竖彩条的宽度比为3∶2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?
③ ④
①
②
归纳概念
与几何图形有关的一元二次方程的应用题主要是将数字及数字间的关系隐藏在图形中,用图形表示出来,这样的图形主要有三角形、四边形等,涉及到三角形的三边关系、三角形全等、面积的计算、体积的计算、勾股定理等.
课堂练习
1.从正方形铁片的边截去2cm宽的一个长方形,余下的
面积是48cm2,则原来的正方形铁片的面积是( )
A.8cm B.64cm C.8cm2 D.64cm2
D
2.如图所示,在一边靠墙(墙足够长)的空地上,修建一个
面积为 640 的矩形临时仓库,仓库一边靠墙,另三边用总长为
80m的栅栏围成,若设栅栏 AB 的长为 x m,则根据题意可列
方程_______________.
x2-80x+1280=0
A
B
x
3.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
解:设道路宽为x米.
由题意知:(32-2x)(20-x)=570
解得 x1=1 ,x2=35(舍)
答:道路宽为1米.
4. 小林准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
解:(1)设其中一个小正方形的边长为x cm,则另一个小正
方形的边长为 =(10-x)cm.
依题意x2+(10-x)2=58,解得x1=3,x2=7.
当x=3时,小正方形周长为12cm;
当x=7时,小正方形周长为28cm.
∴小林应把长为40cm的铁丝剪为28cm和12cm的两段.
(2)对.两个正方形的面积之和为:
x2+(10-x)2=2x2-20x+100
=2(x2-10x+25)+50=2(x-5)2+50
∵无论x取何值,2(x-5)2总是不小于0的.
∴2(x-5)2+50≥50.即这两个正方形的面积之和总是不小于50cm2的,所以不可能等于48cm2.
小峰的说法是对的.
课堂总结
课堂总结
几何图形与一元二次方程问题
几何图形
常见几何图形面积是等量关系.
类 型
课本封面问题
彩条/小路宽度问题
常采用图形平移能聚零为整方便列方程
销售问题
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.3.1 实际问题与一元二次方程(3)
人教版九年级上册
教学目标
教学目标:1.能根据实际问题中的数量关系,正确列出一元二次方程;
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
教学重点:列一元二次方程解有关特殊图形的应用题.
教学难点:发现特殊图形问题中的等量关系.
新知导入
情境引入
探究:要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度
(结果保留小数点后一位)
新知讲解
合作学习
分析:封面的长宽之比是
9∶7,中央的矩形的长宽之比也应是 9∶7.
27
21
9a
7a
设中央的矩形的长和宽分别是 9a cm和 7a cm,由此得上、下边衬与左、右边衬的宽度之比是
( )
( )
27 - 9a ∶ 21 - 7a = 9∶7.
整理得:16y 2 - 48y + 9 = 0.
解法一:设上、下边衬的宽均为 9y cm,左、右边
衬宽均为 7y cm,依题意得
方程的哪个根合乎实际意义?为什么?
解方程得
≈1.8 cm,
≈1.4 cm.
( )
( )
27 - 18y 21 - 14y
试一试:如果换一种设未知数的方法,是否可以更简单地解决上面的问题?
解法二:设正中央的矩形两边分别为 9x cm,7x cm,
依题意得
故上、下边衬的宽度为:
解得: , (不合题意,舍去).
左、右边衬的宽度为:
≈1.8 cm,
( )
≈1.4 cm.
( )
提炼概念
几何图形主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程.
典例精讲
例 如图,要设计一幅宽20cm,长30cm的图案,其中有两横、两竖的彩条,横、竖彩条的宽度比为3∶2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?
③ ④
①
②
归纳概念
与几何图形有关的一元二次方程的应用题主要是将数字及数字间的关系隐藏在图形中,用图形表示出来,这样的图形主要有三角形、四边形等,涉及到三角形的三边关系、三角形全等、面积的计算、体积的计算、勾股定理等.
课堂练习
1.从正方形铁片的边截去2cm宽的一个长方形,余下的
面积是48cm2,则原来的正方形铁片的面积是( )
A.8cm B.64cm C.8cm2 D.64cm2
D
2.如图所示,在一边靠墙(墙足够长)的空地上,修建一个
面积为 640 的矩形临时仓库,仓库一边靠墙,另三边用总长为
80m的栅栏围成,若设栅栏 AB 的长为 x m,则根据题意可列
方程_______________.
x2-80x+1280=0
A
B
x
3.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
解:设道路宽为x米.
由题意知:(32-2x)(20-x)=570
解得 x1=1 ,x2=35(舍)
答:道路宽为1米.
4. 小林准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
解:(1)设其中一个小正方形的边长为x cm,则另一个小正
方形的边长为 =(10-x)cm.
依题意x2+(10-x)2=58,解得x1=3,x2=7.
当x=3时,小正方形周长为12cm;
当x=7时,小正方形周长为28cm.
∴小林应把长为40cm的铁丝剪为28cm和12cm的两段.
(2)对.两个正方形的面积之和为:
x2+(10-x)2=2x2-20x+100
=2(x2-10x+25)+50=2(x-5)2+50
∵无论x取何值,2(x-5)2总是不小于0的.
∴2(x-5)2+50≥50.即这两个正方形的面积之和总是不小于50cm2的,所以不可能等于48cm2.
小峰的说法是对的.
课堂总结
课堂总结
几何图形与一元二次方程问题
几何图形
常见几何图形面积是等量关系.
类 型
课本封面问题
彩条/小路宽度问题
常采用图形平移能聚零为整方便列方程
销售问题
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
