吉林省长春市朝阳区2021-2022第二学期九年级第三次月考数学试题(PDF版,无答案)
文档属性
| 名称 | 吉林省长春市朝阳区2021-2022第二学期九年级第三次月考数学试题(PDF版,无答案) | 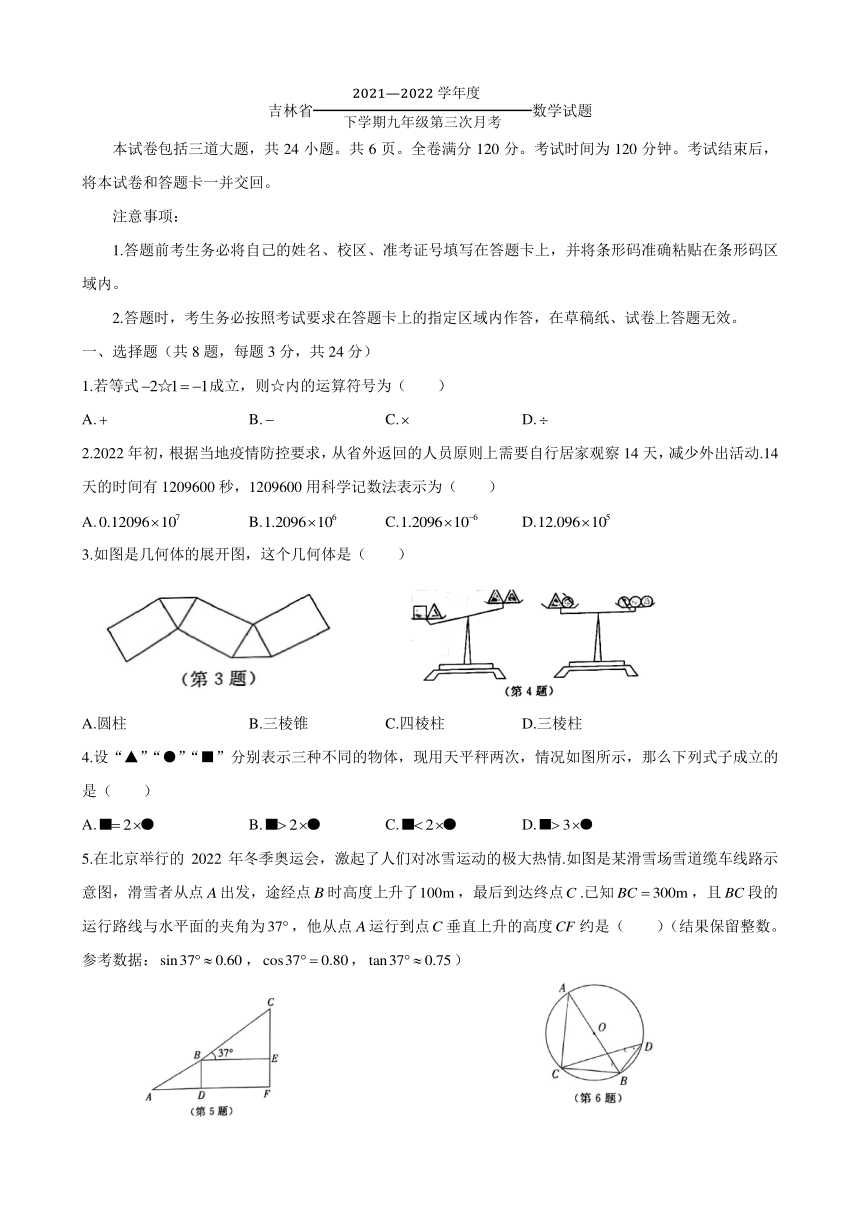 | |
| 格式 | |||
| 文件大小 | 976.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 15:35:39 | ||
图片预览


文档简介
2021—2022学年度
吉林省 数学试题
下学期九年级第三次月考
本试卷包括三道大题,共 24 小题。共 6 页。全卷满分 120 分。考试时间为 120 分钟。考试结束后,
将本试卷和答题卡一并交回。
注意事项:
1.答题前考生务必将自己的姓名、校区、准考证号填写在答题卡上,并将条形码准确粘贴在条形码区
域内。
2.答题时,考生务必按照考试要求在答题卡上的指定区域内作答,在草稿纸、试卷上答题无效。
一、选择题(共 8 题,每题 3 分,共 24 分)
1.若等式 2☆1 1成立,则☆内的运算符号为( )
A. B. C. D.
2.2022 年初,根据当地疫情防控要求,从省外返回的人员原则上需要自行居家观察 14 天,减少外出活动.14
天的时间有 1209600 秒,1209600 用科学记数法表示为( )
A. 0.12096 107 B.1.2096 106 C.1.2096 10 6 D.12.096 105
3.如图是几何体的展开图,这个几何体是( )
A.圆柱 B.三棱锥 C.四棱柱 D.三棱柱
4.设“▲”“●”“■”分别表示三种不同的物体,现用天平秤两次,情况如图所示,那么下列式子成立的
是( )
A.■ 2 ● B.■ 2 ● C.■ 2 ● D.■ 3 ●
5.在北京举行的 2022 年冬季奥运会,激起了人们对冰雪运动的极大热情.如图是某滑雪场雪道缆车线路示
意图,滑雪者从点 A出发,途经点 B 时高度上升了100m ,最后到达终点C .已知 BC 300m ,且 BC 段的
运行路线与水平面的夹角为 37 ,他从点 A运行到点C 垂直上升的高度CF 约是( )(结果保留整数。
参考数据: sin37 0.60 , cos37 0.80, tan37 0.75)
A. 280m B. 300m C. 325m D. 340m
6.如图,△ABC与△BCD是⊙O的内接三角形,AB 是⊙O的直径,且 ABC 50 ,则 D 的度数是( )
A. 40 B. 50 C. 20 D. 25
7.如图是甲和乙两位同学用尺规作 AOB的平分线的图示,对于两人不同的作法下列说法正确的是( )
A.甲对乙不对 B.甲乙都对 C.甲不对乙对 D.甲乙都不对
8.在平面直角坐标系 xOy 中,矩形OBCD的顶点B 在 x 轴正半轴上,顶点 D 在 y 轴正半轴上.如图,若反比
k
例函数 y x 0 的图象与CD交于点 M ,与 BC 交于点 N ,CM 2DM ,连接OM ,ON ,MN ,则
x
S
△CMN ( )
S△OMN
1 1 1
A. B. C. D.1
4 3 2
二、填空题(共 6 题,每题 3 分,共 18 分)
9.在实数范围内因式分解: 4a5 4a ________.
10.如图,△ABC与△A1B1C1 位似,位似中心是点O,则OA :OA 1 1:2 ,△ABC的面积为 3,则△A1B1C1 的
面积是________.
11.若关于 x 的一元二次方程 x2 4x m 1有两个相等的实数根,则实数m 的值是________.
12.如图,正五边形 ABCDE 内接于⊙O,若⊙O的半径为 5,则劣弧 AC 的长为________(结果保留 )
13.如图,矩形 ABCD中,AD 18,AB 24 .点E 为边 DC 上的一个动点,△AD E 与△ADE 关于直线 AE
对称,当 CD E 为直角时, DE 的长为________.
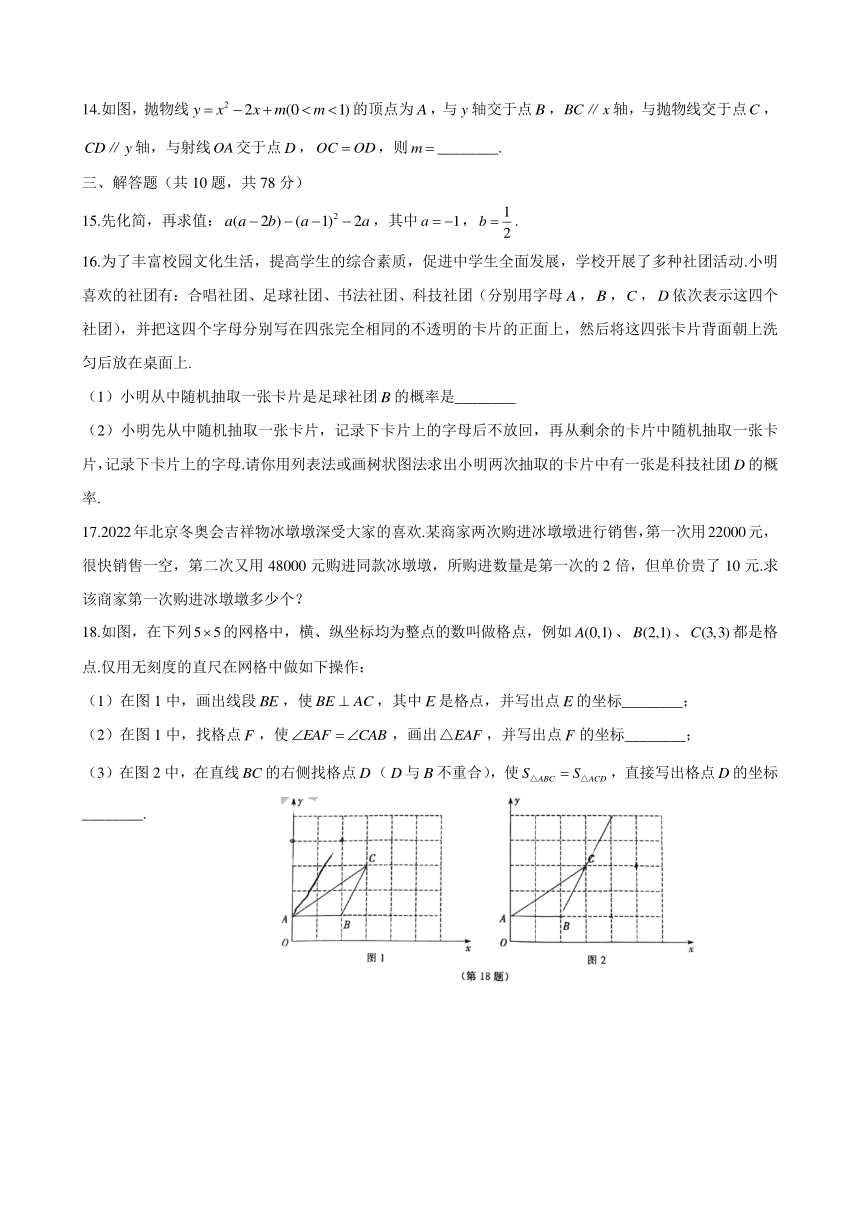
14.如图,抛物线 y x2 2x m(0 m 1)的顶点为 A,与 y 轴交于点B ,BC∥x 轴,与抛物线交于点C ,
CD∥ y 轴,与射线OA交于点 D ,OC OD,则m ________.
三、解答题(共 10 题,共 78 分)
1
15.先化简,再求值: a(a 2b) (a 1)2 2a,其中 a 1,b .
2
16.为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明
喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母 A,B ,C ,D 依次表示这四个
社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗
匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B 的概率是________
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡
片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团 D 的概
率.
17.2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,
很快销售一空,第二次又用 48000 元购进同款冰墩墩,所购进数量是第一次的 2 倍,但单价贵了 10 元.求
该商家第一次购进冰墩墩多少个?
18.如图,在下列5 5的网格中,横、纵坐标均为整点的数叫做格点,例如 A(0,1)、 B(2,1)、C(3,3)都是格
点.仅用无刻度的直尺在网格中做如下操作:
(1)在图 1 中,画出线段 BE ,使 BE AC ,其中E 是格点,并写出点E 的坐标________;
(2)在图 1 中,找格点 F ,使 EAF CAB ,画出△EAF ,并写出点 F 的坐标________;
(3)在图 2 中,在直线 BC 的右侧找格点 D(D 与 B 不重合),使 S△ABC S△ACD ,直接写出格点D 的坐标
________.
19.如图△ABC中 BCA 90 ,CD是边 AB 上的中线,分别过点C ,D 作 BA, BC 的平行线交于点E ,
且 DE 交 AC 于点O,连接 AE .
(1)求证:四边形 ADCE 是菱形;
(2)若 AC 2DE ,求 sin CDB ________.
20.为庆祝中国共产党建党 100 周年,某校开展了以“学习百年党史,汇聚团结伟力”为主题的知识竞赛,
竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成 A, B ,C , D , E 五个等级,并绘制了如
下不完整的统计图.请结合统计图,解答下列问题:
等级 成绩 x
A 50 x 60
B 60 x 70
C 70 x 80
D 80 x 90
E 90 x 100
(1)本次调查一共随机抽取了________名学生的成绩,频数分布直方图中m ________;
(2)补全学生成绩频数分布直方图;
(3)所抽取学生成绩的中位数落在________等级;
(4)若成绩在 80 分及以上为优秀,全校共有 2000 名学生,估计成绩优秀的学生有多少人?
21.甲、乙两地间的直线公路长为 180 千米、一辆摩托车和一辆轿车分别从甲、乙两地出发,沿该公路匀速
行驶,已知轿车比摩托车早出发 1 小时,且轿车到达甲地停留 t 小时后原路原速返回甲地(调头时间忽略
不计),最后两车同时到达乙地,在行驶过程中,两车距乙地的距离 y(千米)与摩托车行驶的时间 x(小
时)的关系如图所示,请结合图象信息解答下列问题:
(1)轿车的速度是________千米/小时、摩托车的速度是________千米/小时, t 的值为________;
(2)写出摩托车距乙地的距离 y (千米)与 x (小时)的关系式;
(3)摩托车出发后几小时,两车在途中相距 30 千米?请直接写出答案.
22.(9 分)在水平方向的一条线段 AB 上取一点 P ,(点 P 不与 A、B 重合),分别以 AP 、BP为边在 AB
上方作正方形 APEF 和正方形 BPDC ,连结 AE 、 BD,并取分别线段 AE 、 BD的中点M 、 N .
(1)①【特殊】
如图 1,已知线段 AB 的长为 12,当点 P 为靠近 A的三等分点时,则线段MN 的长为________.
②【一般】
已知线段 AB 的长为 12,求线段MN 的最小值.
(2)【灵活运用】
如图 3,在△ABC中,AB 10 ,BC 8,AC 6,点P 在边 AC 上(点P 不与点 A重合),以P 为圆心,
PA长为半径作圆,与线段 AB 的另一个交点为点D ,DQ 切圆P 于点 D ,交 BC 于点Q,则线段 PQ的最
小值为________.
23.如图,在Rt△ABC 中, C 90 , A 60 , AB 4cm .动点P 从点 A出发,以1cm/s 的速度沿边 AB
向终点 B 运动.过点 P 作 PQ AB交直线 AC 于点Q,为 PQ为边向右侧作矩形 PQMN ,使QM 3PQ .
点 P 的运动时间为 t(s)(0 t 4) .
(1)当点Q在边 AC 上时,求QM 的长(用含 t 的代数式表示).
(2)当点M 在边 BC 上时,求 t 的值.
(3)作射线PM 交 BC 于点 D ,连接QN ,当QN 3DM 时,求 t 的值.
(4)连结 BQ,沿直线 BQ将矩形 PQMN 剪开的两部分可以拼成一个无缝隙也不重叠的三角形时,直接写
出 t 的值.
24.(12 分)在平面直角坐标系 xoy中,点 A、B 均在抛物线 y x2 mx 2m 4上,且点 A、B 的横坐标
分别为m 4 和m 4 .
(1)当m 4时,求此时的顶点坐标.
(2)当点 A的纵坐标小于点 B 的纵坐标时,求此时m 的取值范围.
(3)分别过点 A、 B 作 x 轴的垂线,和 x 轴交于D 、C 两点,以 DC 为边向上作正方形CDEF .
①当m 4 时,抛物线在正方形CDEF 内部(包括边界)的函数部分的最高点的纵坐标与最低点的纵坐标
之差为定值时,求m 的取值范围.
②当抛物线与正方形CDEF 的边只有两个交点时,并且这两个交点到抛物线的对称轴的距离之和为 5,直
接写出此时m 的值.
吉林省 数学试题
下学期九年级第三次月考
本试卷包括三道大题,共 24 小题。共 6 页。全卷满分 120 分。考试时间为 120 分钟。考试结束后,
将本试卷和答题卡一并交回。
注意事项:
1.答题前考生务必将自己的姓名、校区、准考证号填写在答题卡上,并将条形码准确粘贴在条形码区
域内。
2.答题时,考生务必按照考试要求在答题卡上的指定区域内作答,在草稿纸、试卷上答题无效。
一、选择题(共 8 题,每题 3 分,共 24 分)
1.若等式 2☆1 1成立,则☆内的运算符号为( )
A. B. C. D.
2.2022 年初,根据当地疫情防控要求,从省外返回的人员原则上需要自行居家观察 14 天,减少外出活动.14
天的时间有 1209600 秒,1209600 用科学记数法表示为( )
A. 0.12096 107 B.1.2096 106 C.1.2096 10 6 D.12.096 105
3.如图是几何体的展开图,这个几何体是( )
A.圆柱 B.三棱锥 C.四棱柱 D.三棱柱
4.设“▲”“●”“■”分别表示三种不同的物体,现用天平秤两次,情况如图所示,那么下列式子成立的
是( )
A.■ 2 ● B.■ 2 ● C.■ 2 ● D.■ 3 ●
5.在北京举行的 2022 年冬季奥运会,激起了人们对冰雪运动的极大热情.如图是某滑雪场雪道缆车线路示
意图,滑雪者从点 A出发,途经点 B 时高度上升了100m ,最后到达终点C .已知 BC 300m ,且 BC 段的
运行路线与水平面的夹角为 37 ,他从点 A运行到点C 垂直上升的高度CF 约是( )(结果保留整数。
参考数据: sin37 0.60 , cos37 0.80, tan37 0.75)
A. 280m B. 300m C. 325m D. 340m
6.如图,△ABC与△BCD是⊙O的内接三角形,AB 是⊙O的直径,且 ABC 50 ,则 D 的度数是( )
A. 40 B. 50 C. 20 D. 25
7.如图是甲和乙两位同学用尺规作 AOB的平分线的图示,对于两人不同的作法下列说法正确的是( )
A.甲对乙不对 B.甲乙都对 C.甲不对乙对 D.甲乙都不对
8.在平面直角坐标系 xOy 中,矩形OBCD的顶点B 在 x 轴正半轴上,顶点 D 在 y 轴正半轴上.如图,若反比
k
例函数 y x 0 的图象与CD交于点 M ,与 BC 交于点 N ,CM 2DM ,连接OM ,ON ,MN ,则
x
S
△CMN ( )
S△OMN
1 1 1
A. B. C. D.1
4 3 2
二、填空题(共 6 题,每题 3 分,共 18 分)
9.在实数范围内因式分解: 4a5 4a ________.
10.如图,△ABC与△A1B1C1 位似,位似中心是点O,则OA :OA 1 1:2 ,△ABC的面积为 3,则△A1B1C1 的
面积是________.
11.若关于 x 的一元二次方程 x2 4x m 1有两个相等的实数根,则实数m 的值是________.
12.如图,正五边形 ABCDE 内接于⊙O,若⊙O的半径为 5,则劣弧 AC 的长为________(结果保留 )
13.如图,矩形 ABCD中,AD 18,AB 24 .点E 为边 DC 上的一个动点,△AD E 与△ADE 关于直线 AE
对称,当 CD E 为直角时, DE 的长为________.
14.如图,抛物线 y x2 2x m(0 m 1)的顶点为 A,与 y 轴交于点B ,BC∥x 轴,与抛物线交于点C ,
CD∥ y 轴,与射线OA交于点 D ,OC OD,则m ________.
三、解答题(共 10 题,共 78 分)
1
15.先化简,再求值: a(a 2b) (a 1)2 2a,其中 a 1,b .
2
16.为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明
喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母 A,B ,C ,D 依次表示这四个
社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗
匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B 的概率是________
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡
片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团 D 的概
率.
17.2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,
很快销售一空,第二次又用 48000 元购进同款冰墩墩,所购进数量是第一次的 2 倍,但单价贵了 10 元.求
该商家第一次购进冰墩墩多少个?
18.如图,在下列5 5的网格中,横、纵坐标均为整点的数叫做格点,例如 A(0,1)、 B(2,1)、C(3,3)都是格
点.仅用无刻度的直尺在网格中做如下操作:
(1)在图 1 中,画出线段 BE ,使 BE AC ,其中E 是格点,并写出点E 的坐标________;
(2)在图 1 中,找格点 F ,使 EAF CAB ,画出△EAF ,并写出点 F 的坐标________;
(3)在图 2 中,在直线 BC 的右侧找格点 D(D 与 B 不重合),使 S△ABC S△ACD ,直接写出格点D 的坐标
________.
19.如图△ABC中 BCA 90 ,CD是边 AB 上的中线,分别过点C ,D 作 BA, BC 的平行线交于点E ,
且 DE 交 AC 于点O,连接 AE .
(1)求证:四边形 ADCE 是菱形;
(2)若 AC 2DE ,求 sin CDB ________.
20.为庆祝中国共产党建党 100 周年,某校开展了以“学习百年党史,汇聚团结伟力”为主题的知识竞赛,
竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成 A, B ,C , D , E 五个等级,并绘制了如
下不完整的统计图.请结合统计图,解答下列问题:
等级 成绩 x
A 50 x 60
B 60 x 70
C 70 x 80
D 80 x 90
E 90 x 100
(1)本次调查一共随机抽取了________名学生的成绩,频数分布直方图中m ________;
(2)补全学生成绩频数分布直方图;
(3)所抽取学生成绩的中位数落在________等级;
(4)若成绩在 80 分及以上为优秀,全校共有 2000 名学生,估计成绩优秀的学生有多少人?
21.甲、乙两地间的直线公路长为 180 千米、一辆摩托车和一辆轿车分别从甲、乙两地出发,沿该公路匀速
行驶,已知轿车比摩托车早出发 1 小时,且轿车到达甲地停留 t 小时后原路原速返回甲地(调头时间忽略
不计),最后两车同时到达乙地,在行驶过程中,两车距乙地的距离 y(千米)与摩托车行驶的时间 x(小
时)的关系如图所示,请结合图象信息解答下列问题:
(1)轿车的速度是________千米/小时、摩托车的速度是________千米/小时, t 的值为________;
(2)写出摩托车距乙地的距离 y (千米)与 x (小时)的关系式;
(3)摩托车出发后几小时,两车在途中相距 30 千米?请直接写出答案.
22.(9 分)在水平方向的一条线段 AB 上取一点 P ,(点 P 不与 A、B 重合),分别以 AP 、BP为边在 AB
上方作正方形 APEF 和正方形 BPDC ,连结 AE 、 BD,并取分别线段 AE 、 BD的中点M 、 N .
(1)①【特殊】
如图 1,已知线段 AB 的长为 12,当点 P 为靠近 A的三等分点时,则线段MN 的长为________.
②【一般】
已知线段 AB 的长为 12,求线段MN 的最小值.
(2)【灵活运用】
如图 3,在△ABC中,AB 10 ,BC 8,AC 6,点P 在边 AC 上(点P 不与点 A重合),以P 为圆心,
PA长为半径作圆,与线段 AB 的另一个交点为点D ,DQ 切圆P 于点 D ,交 BC 于点Q,则线段 PQ的最
小值为________.
23.如图,在Rt△ABC 中, C 90 , A 60 , AB 4cm .动点P 从点 A出发,以1cm/s 的速度沿边 AB
向终点 B 运动.过点 P 作 PQ AB交直线 AC 于点Q,为 PQ为边向右侧作矩形 PQMN ,使QM 3PQ .
点 P 的运动时间为 t(s)(0 t 4) .
(1)当点Q在边 AC 上时,求QM 的长(用含 t 的代数式表示).
(2)当点M 在边 BC 上时,求 t 的值.
(3)作射线PM 交 BC 于点 D ,连接QN ,当QN 3DM 时,求 t 的值.
(4)连结 BQ,沿直线 BQ将矩形 PQMN 剪开的两部分可以拼成一个无缝隙也不重叠的三角形时,直接写
出 t 的值.
24.(12 分)在平面直角坐标系 xoy中,点 A、B 均在抛物线 y x2 mx 2m 4上,且点 A、B 的横坐标
分别为m 4 和m 4 .
(1)当m 4时,求此时的顶点坐标.
(2)当点 A的纵坐标小于点 B 的纵坐标时,求此时m 的取值范围.
(3)分别过点 A、 B 作 x 轴的垂线,和 x 轴交于D 、C 两点,以 DC 为边向上作正方形CDEF .
①当m 4 时,抛物线在正方形CDEF 内部(包括边界)的函数部分的最高点的纵坐标与最低点的纵坐标
之差为定值时,求m 的取值范围.
②当抛物线与正方形CDEF 的边只有两个交点时,并且这两个交点到抛物线的对称轴的距离之和为 5,直
接写出此时m 的值.
同课章节目录
