吉林省长春市北湖学校2021-2022学年第二学期九年级数学5月质量调研试题(PDF版,无答案)
文档属性
| 名称 | 吉林省长春市北湖学校2021-2022学年第二学期九年级数学5月质量调研试题(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 15:34:54 | ||
图片预览

文档简介
长春市十一高中北湖学校九年级 2021-2022 学年度下学期
数学学科质量调研测试
日期:5月 13 日
一、选择题(本大题共 8小题,共 24 分)
1. 如图表示互为相反数的两个点是( )
A. 点 与点 B. 点 与点 C. 点 与点 D. 点 与点
2. 随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,去年“双十一”天猫成
交额高达 2684亿元.将数据“2684亿”用科学记数法表示( )
A. 2.684 × 103 B. 2.684 × 1011 C. 2.684 × 1012 D. 2.684 × 107
3. 下列立体图形中,主视图和左视图不一样的是( )
A. B. C. D.
4. 2 < + 4不等式组 3 + ≥ 3 + 9 的解集在数轴上用阴影表示正确的是( )
A. B. C. D.
5. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一
房空.”诗中后两句的意思是:如果每一间客房住 7人,那么有 7人无房住;如果每一间客房住 9人,那么就
空出一间客房.设该店有客房 间、房客 人,下列方程组中正确的是( )
A. 7 + 7 = B. 7 + 7 = 7 7 = 7 7 = 9( 1) = 9( + 1) = C. 9( 1) = D. 9( + 1) =
6. 如图,长春市某小区核酸检测站屋顶人字架的跨度 = 12 ,上弦 = ,
∠ = 25°.若用科学计算器求上弦 的长,则下列按键顺序正确的是( )
A. B.
C. D.
7. 如图,在 中,∠ = 90°,∠ = 30°,以 为圆心,任意长为半径画弧分别交 ,
于点 和 1,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,
2
连接 并延长交 于点 ,则下列说法中错误的是( )
A. 点 在 的中垂线上 B. = 2
C. 点 到∠ 两边的距离相等 D. = 6
8. 12如图, 为第一象限内一点,过 作 // 轴, // 轴,分别交函数 = 于 ,
两点,若 △ = 4,则 △ 为( )
A. 12 B. 14 C. 16 D. 18
1
二、填空题(本大题共 6 小题,共 18 分)
9. 计算 3 × 2 6的结果是 .
10. 因式分解:4 2 25 = .
11. 若关于 的一元二次方程 2 2 + = 0有两个相等的实数根,则 的值是 .
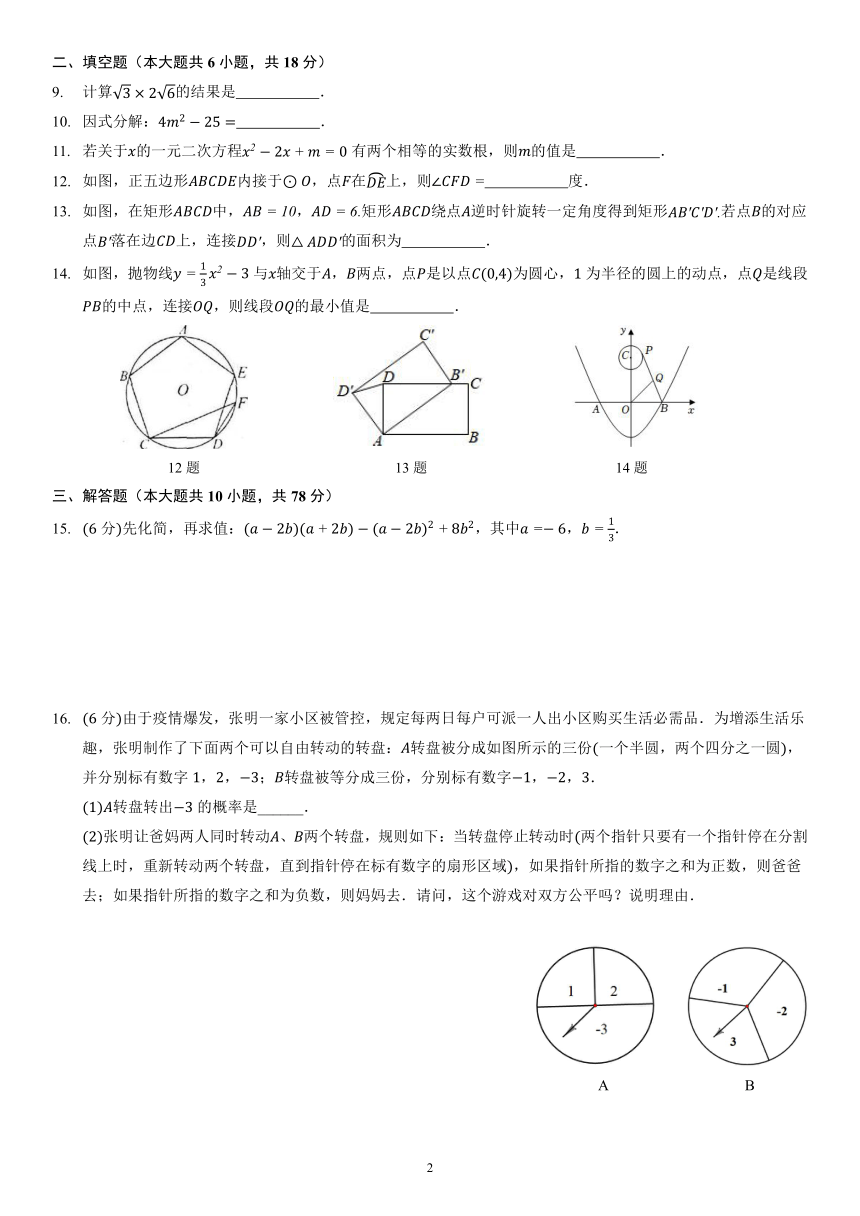
12. 如图,正五边形 内接于⊙ ,点 在 � 上,则∠ = 度.
13. 如图,在矩形 中, = 10, = 6.矩形 绕点 逆时针旋转一定角度得到矩形 ′ ′ ′.若点 的对应
点 ′落在边 上,连接 ′,则△ ′的面积为 .
14. 1如图,抛物线 = 2 3与 轴交于 , 两点,点 是以点 (0,4)为圆心,1为半径的圆上的动点,点 是线段
3
的中点,连接 ,则线段 的最小值是 .
12题 13题 14题
三、解答题(本大题共 10 小题,共 78 分)
15. (6分)先化简,再求值:( 2 )( + 2 ) ( 2 )2 + 8 2,其中 = 6, = 1.
3
16. (6分)由于疫情爆发,张明一家小区被管控,规定每两日每户可派一人出小区购买生活必需品.为增添生活乐
趣,张明制作了下面两个可以自由转动的转盘: 转盘被分成如图所示的三份(一个半圆,两个四分之一圆),
并分别标有数字 1,2, 3; 转盘被等分成三份,分别标有数字 1, 2,3.
(1) 转盘转出 3的概率是______.
(2)张明让爸妈两人同时转动 、 两个转盘,规则如下:当转盘停止转动时(两个指针只要有一个指针停在分割
线上时,重新转动两个转盘,直到指针停在标有数字的扇形区域),如果指针所指的数字之和为正数,则爸爸
去;如果指针所指的数字之和为负数,则妈妈去.请问,这个游戏对双方公平吗?说明理由.
A B
2
17. (6分)2022年北京冬奥会是我国又一次举办的大型国际奥林匹克运动盛会.为了增加学生相关知识,某校开展
“冬奥会知识竞赛”活动并计划购买大小两种型号的吉祥物玩偶作为奖品.已知大型号的单价比小型号的单价
多 16元,且学校用 1950元购买小型号的数量是用 1050元购买大型号数量的三倍.求两种型号玩偶的单价
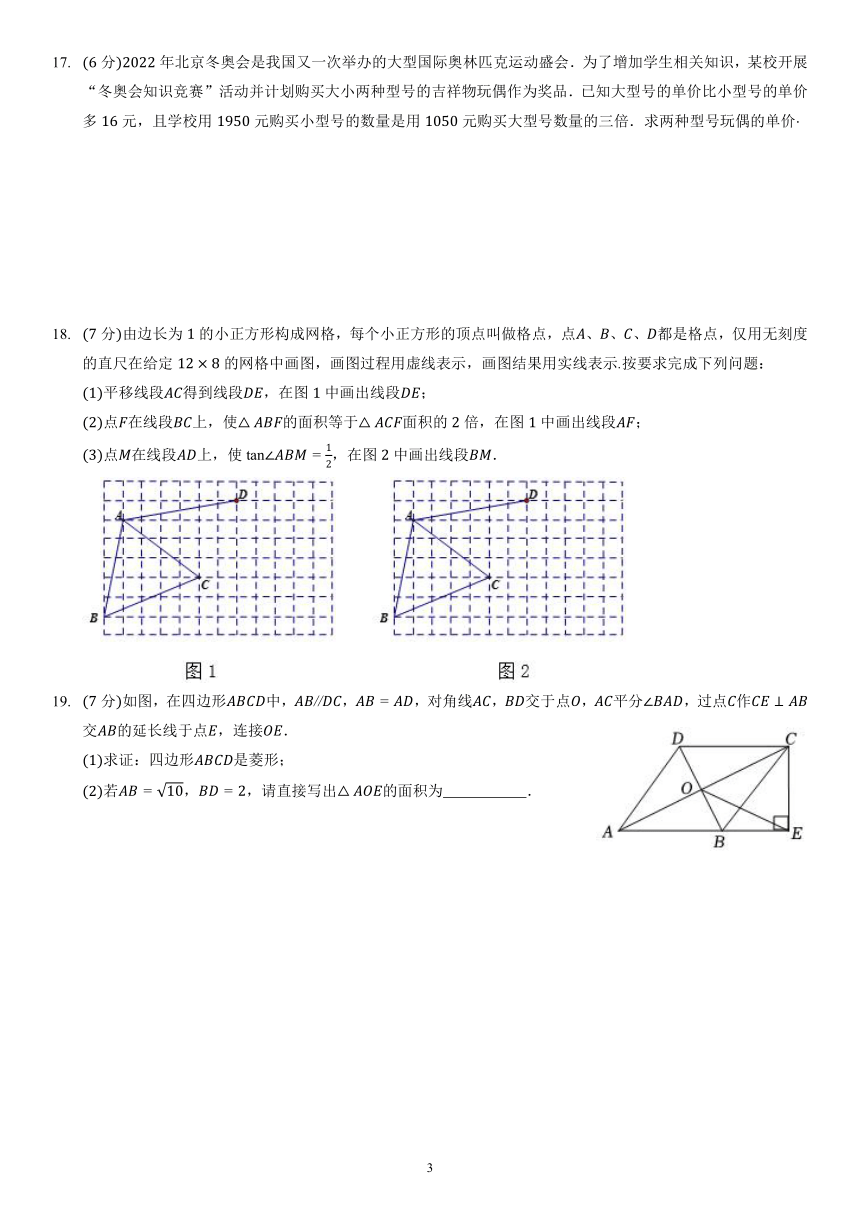
18. (7分)由边长为 1的小正方形构成网格,每个小正方形的顶点叫做格点,点 、 、 、 都是格点,仅用无刻度
的直尺在给定 12 × 8的网格中画图,画图过程用虚线表示,画图结果用实线表示.按要求完成下列问题:
(1)平移线段 得到线段 ,在图 1中画出线段 ;
(2)点 在线段 上,使△ 的面积等于△ 面积的 2倍,在图 1中画出线段 ;
(3)点 在线段 上,使 tan∠ = 1,在图 2中画出线段 .
2
19. (7分)如图,在四边形 中, // , = ,对角线 , 交于点 , 平分∠ ,过点 作 ⊥
交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若 = 10, = 2,请直接写出△ 的面积为 .
3
20. (7分)为了解某地区企业信息化发展水平,从该地区中随机抽取 50家企业调研,针对体现企业信息化发展水平
的 和 两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了
部分信息.
. A项指标成绩的频数分布直方图如图(数据分成 6组:4 ≤ < 5,5 ≤ < 6,6 ≤ < 7,7 ≤ < 8,8 ≤ < 9,
9 ≤ ≤ 10):
. A项指标成绩在 7 ≤ < 8 这一组的是:
7.2,7.3,7.5,7.67,7.7,7.71,7.75,7.82,7.86,7.9,7.92,7.93,7.97.
. A、B两项指标成绩的平均数、中位数、众数如下:
平均数 中位数 众数
A项指标成绩 7.37 8.2
B项指标成绩 7.21 7.3 8
根据以上信息,回答下列问题:
(1)写出表中 的值;
(2)在此次调研评估中,某企业 项指标成绩和 项指标成绩都是 7.5分,该企业成绩排名更靠前的指标是
(填“ “或“ ”),理由是 ;
(3)如果该地区有 500 家企业,估计 项指标成绩超过 7.68分的企业数量.
21. (8分)甲乙两人相约一起去登山,登山过程中,甲先爬了 100 米、乙才开始追赶甲。甲、乙两人距地面的高度
(米)与登山时间 (分)( ≥0)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙提速时距地面的高度 为 米;
(2)若乙提速后,乙的速度是甲登山速度的 3 倍,请求出整个登山过程中乙距离地面的高度 (米)与登山时间
(分)之间的函数关系,并写出相应自变量取值范围.
(3)直接写出甲乙相遇后,甲再经过多长时间与乙相距 30米?
4
22. (9分)【教材呈现】如图是华师版九年级上册数学教材第 77页的部分内容:
如图,在△ 中,点 、 分别是 与 的中点,可以猜想: //
且 = 1 .请写出证明过程.
2
【结论应用】
(1)如图 1,四边形 中, = , 、 、 分别是 、 、 的中点.若∠ = 80°,∠ = 20°,
求∠ 的度数.
(2)如图 2,在△ 外分别作正方形 和 , 是 的中点, , 分别是正方形的中心, = 6, = 4,
则△ 的面积最大值为______.
23. (10分)如图,在 △ 中,∠ = 90°, = 8, = 4,点 从点 出发,以每秒 2 5个单位长度的速度沿
向点 运动,(点 与点 、 不重合),过点 作 ⊥ 交边 或边 于点 ,点 是射线 上的一点,且 =
2 ,以 、 为邻边作矩形 .设点 的运动时间为 (秒).
(1)用含 的代数式表示线段 的长.
(2)当点 落在 上时,求 的值.
(3)当矩形 与△ 重叠部分图形为四边形时,求 的取值范围.
(4)若△ 重心为 ,矩形 中心为 ,当点 与点 到直线 距离相同时,请直接写出 的值.
5
24. (12分)在平面直角坐标系中,抛物线 = 2 2 ( 为常数).
(1)当( 1 , )在抛物线上,求 的值.
2
1 1
(2)当抛物线的最低点到直线 y - 的距离恰好是 时,求 a的值.
2 4
(3)已知 ( 1,1)、 ( 1,2 1 ),连接 .当抛物线与线段 有交点时,记交点为 (点 不与 、 重合),将
2
线段 绕点 顺时针旋转 90°得到线段 ,以 、 为邻边构造矩形 .
①若抛物线在矩形 内部的图象的函数值 随自变量 的增大而减小时,求 的取值范围.
②当抛物线在矩形 内部( 3包含边界)图象所对应的函数的最大值与最小值的差为 时,直接写出 的值.
2
6
数学学科质量调研测试
日期:5月 13 日
一、选择题(本大题共 8小题,共 24 分)
1. 如图表示互为相反数的两个点是( )
A. 点 与点 B. 点 与点 C. 点 与点 D. 点 与点
2. 随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,去年“双十一”天猫成
交额高达 2684亿元.将数据“2684亿”用科学记数法表示( )
A. 2.684 × 103 B. 2.684 × 1011 C. 2.684 × 1012 D. 2.684 × 107
3. 下列立体图形中,主视图和左视图不一样的是( )
A. B. C. D.
4. 2 < + 4不等式组 3 + ≥ 3 + 9 的解集在数轴上用阴影表示正确的是( )
A. B. C. D.
5. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一
房空.”诗中后两句的意思是:如果每一间客房住 7人,那么有 7人无房住;如果每一间客房住 9人,那么就
空出一间客房.设该店有客房 间、房客 人,下列方程组中正确的是( )
A. 7 + 7 = B. 7 + 7 = 7 7 = 7 7 = 9( 1) = 9( + 1) = C. 9( 1) = D. 9( + 1) =
6. 如图,长春市某小区核酸检测站屋顶人字架的跨度 = 12 ,上弦 = ,
∠ = 25°.若用科学计算器求上弦 的长,则下列按键顺序正确的是( )
A. B.
C. D.
7. 如图,在 中,∠ = 90°,∠ = 30°,以 为圆心,任意长为半径画弧分别交 ,
于点 和 1,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,
2
连接 并延长交 于点 ,则下列说法中错误的是( )
A. 点 在 的中垂线上 B. = 2
C. 点 到∠ 两边的距离相等 D. = 6
8. 12如图, 为第一象限内一点,过 作 // 轴, // 轴,分别交函数 = 于 ,
两点,若 △ = 4,则 △ 为( )
A. 12 B. 14 C. 16 D. 18
1
二、填空题(本大题共 6 小题,共 18 分)
9. 计算 3 × 2 6的结果是 .
10. 因式分解:4 2 25 = .
11. 若关于 的一元二次方程 2 2 + = 0有两个相等的实数根,则 的值是 .
12. 如图,正五边形 内接于⊙ ,点 在 � 上,则∠ = 度.
13. 如图,在矩形 中, = 10, = 6.矩形 绕点 逆时针旋转一定角度得到矩形 ′ ′ ′.若点 的对应
点 ′落在边 上,连接 ′,则△ ′的面积为 .
14. 1如图,抛物线 = 2 3与 轴交于 , 两点,点 是以点 (0,4)为圆心,1为半径的圆上的动点,点 是线段
3
的中点,连接 ,则线段 的最小值是 .
12题 13题 14题
三、解答题(本大题共 10 小题,共 78 分)
15. (6分)先化简,再求值:( 2 )( + 2 ) ( 2 )2 + 8 2,其中 = 6, = 1.
3
16. (6分)由于疫情爆发,张明一家小区被管控,规定每两日每户可派一人出小区购买生活必需品.为增添生活乐
趣,张明制作了下面两个可以自由转动的转盘: 转盘被分成如图所示的三份(一个半圆,两个四分之一圆),
并分别标有数字 1,2, 3; 转盘被等分成三份,分别标有数字 1, 2,3.
(1) 转盘转出 3的概率是______.
(2)张明让爸妈两人同时转动 、 两个转盘,规则如下:当转盘停止转动时(两个指针只要有一个指针停在分割
线上时,重新转动两个转盘,直到指针停在标有数字的扇形区域),如果指针所指的数字之和为正数,则爸爸
去;如果指针所指的数字之和为负数,则妈妈去.请问,这个游戏对双方公平吗?说明理由.
A B
2
17. (6分)2022年北京冬奥会是我国又一次举办的大型国际奥林匹克运动盛会.为了增加学生相关知识,某校开展
“冬奥会知识竞赛”活动并计划购买大小两种型号的吉祥物玩偶作为奖品.已知大型号的单价比小型号的单价
多 16元,且学校用 1950元购买小型号的数量是用 1050元购买大型号数量的三倍.求两种型号玩偶的单价
18. (7分)由边长为 1的小正方形构成网格,每个小正方形的顶点叫做格点,点 、 、 、 都是格点,仅用无刻度
的直尺在给定 12 × 8的网格中画图,画图过程用虚线表示,画图结果用实线表示.按要求完成下列问题:
(1)平移线段 得到线段 ,在图 1中画出线段 ;
(2)点 在线段 上,使△ 的面积等于△ 面积的 2倍,在图 1中画出线段 ;
(3)点 在线段 上,使 tan∠ = 1,在图 2中画出线段 .
2
19. (7分)如图,在四边形 中, // , = ,对角线 , 交于点 , 平分∠ ,过点 作 ⊥
交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若 = 10, = 2,请直接写出△ 的面积为 .
3
20. (7分)为了解某地区企业信息化发展水平,从该地区中随机抽取 50家企业调研,针对体现企业信息化发展水平
的 和 两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了
部分信息.
. A项指标成绩的频数分布直方图如图(数据分成 6组:4 ≤ < 5,5 ≤ < 6,6 ≤ < 7,7 ≤ < 8,8 ≤ < 9,
9 ≤ ≤ 10):
. A项指标成绩在 7 ≤ < 8 这一组的是:
7.2,7.3,7.5,7.67,7.7,7.71,7.75,7.82,7.86,7.9,7.92,7.93,7.97.
. A、B两项指标成绩的平均数、中位数、众数如下:
平均数 中位数 众数
A项指标成绩 7.37 8.2
B项指标成绩 7.21 7.3 8
根据以上信息,回答下列问题:
(1)写出表中 的值;
(2)在此次调研评估中,某企业 项指标成绩和 项指标成绩都是 7.5分,该企业成绩排名更靠前的指标是
(填“ “或“ ”),理由是 ;
(3)如果该地区有 500 家企业,估计 项指标成绩超过 7.68分的企业数量.
21. (8分)甲乙两人相约一起去登山,登山过程中,甲先爬了 100 米、乙才开始追赶甲。甲、乙两人距地面的高度
(米)与登山时间 (分)( ≥0)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙提速时距地面的高度 为 米;
(2)若乙提速后,乙的速度是甲登山速度的 3 倍,请求出整个登山过程中乙距离地面的高度 (米)与登山时间
(分)之间的函数关系,并写出相应自变量取值范围.
(3)直接写出甲乙相遇后,甲再经过多长时间与乙相距 30米?
4
22. (9分)【教材呈现】如图是华师版九年级上册数学教材第 77页的部分内容:
如图,在△ 中,点 、 分别是 与 的中点,可以猜想: //
且 = 1 .请写出证明过程.
2
【结论应用】
(1)如图 1,四边形 中, = , 、 、 分别是 、 、 的中点.若∠ = 80°,∠ = 20°,
求∠ 的度数.
(2)如图 2,在△ 外分别作正方形 和 , 是 的中点, , 分别是正方形的中心, = 6, = 4,
则△ 的面积最大值为______.
23. (10分)如图,在 △ 中,∠ = 90°, = 8, = 4,点 从点 出发,以每秒 2 5个单位长度的速度沿
向点 运动,(点 与点 、 不重合),过点 作 ⊥ 交边 或边 于点 ,点 是射线 上的一点,且 =
2 ,以 、 为邻边作矩形 .设点 的运动时间为 (秒).
(1)用含 的代数式表示线段 的长.
(2)当点 落在 上时,求 的值.
(3)当矩形 与△ 重叠部分图形为四边形时,求 的取值范围.
(4)若△ 重心为 ,矩形 中心为 ,当点 与点 到直线 距离相同时,请直接写出 的值.
5
24. (12分)在平面直角坐标系中,抛物线 = 2 2 ( 为常数).
(1)当( 1 , )在抛物线上,求 的值.
2
1 1
(2)当抛物线的最低点到直线 y - 的距离恰好是 时,求 a的值.
2 4
(3)已知 ( 1,1)、 ( 1,2 1 ),连接 .当抛物线与线段 有交点时,记交点为 (点 不与 、 重合),将
2
线段 绕点 顺时针旋转 90°得到线段 ,以 、 为邻边构造矩形 .
①若抛物线在矩形 内部的图象的函数值 随自变量 的增大而减小时,求 的取值范围.
②当抛物线在矩形 内部( 3包含边界)图象所对应的函数的最大值与最小值的差为 时,直接写出 的值.
2
6
同课章节目录
