2021--2022年人教版七年级数学下册第十章《数据的收集、整理与描述》单元同步检测试题(含答案)
文档属性
| 名称 | 2021--2022年人教版七年级数学下册第十章《数据的收集、整理与描述》单元同步检测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 700.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章《数据的收集、整理与描述》单元检测题
题号 一 二 三 总分
21 22 23 24 25 26 27 28
分数
一、选择题(本大题共10小题,每小题3分,共计30分)
1.学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
得分 60 70 80 90 100
人数 7 12 10 8 3
得分的众数和中位数分别是( )
A.70,70 B.80,80 C.70,80 D.80,70
2.某球员参加一场篮球比赛,比赛分4节进行,该球员每节的得分如图1所示,则该球员平均每节的得分为( )
1.
2. 图1
A.7分 B.8分 C.9分 D.10分
一个班有40名学生,在期末体育考核中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是( )
A.144° B.162° C.216° D.250°
4.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
A.4,4 B.3,4 C.4,3 D.3,3
5.济南某中学足球队的18名队员的年龄如下表所示:
年龄/岁 12 13 14 15
人数 3 5 6 4
这18名队员年龄的众数和中位数分别是( )
A.13岁,14岁 B.14岁,14岁 C.14岁,13岁 D.14岁,15岁
(第6题)
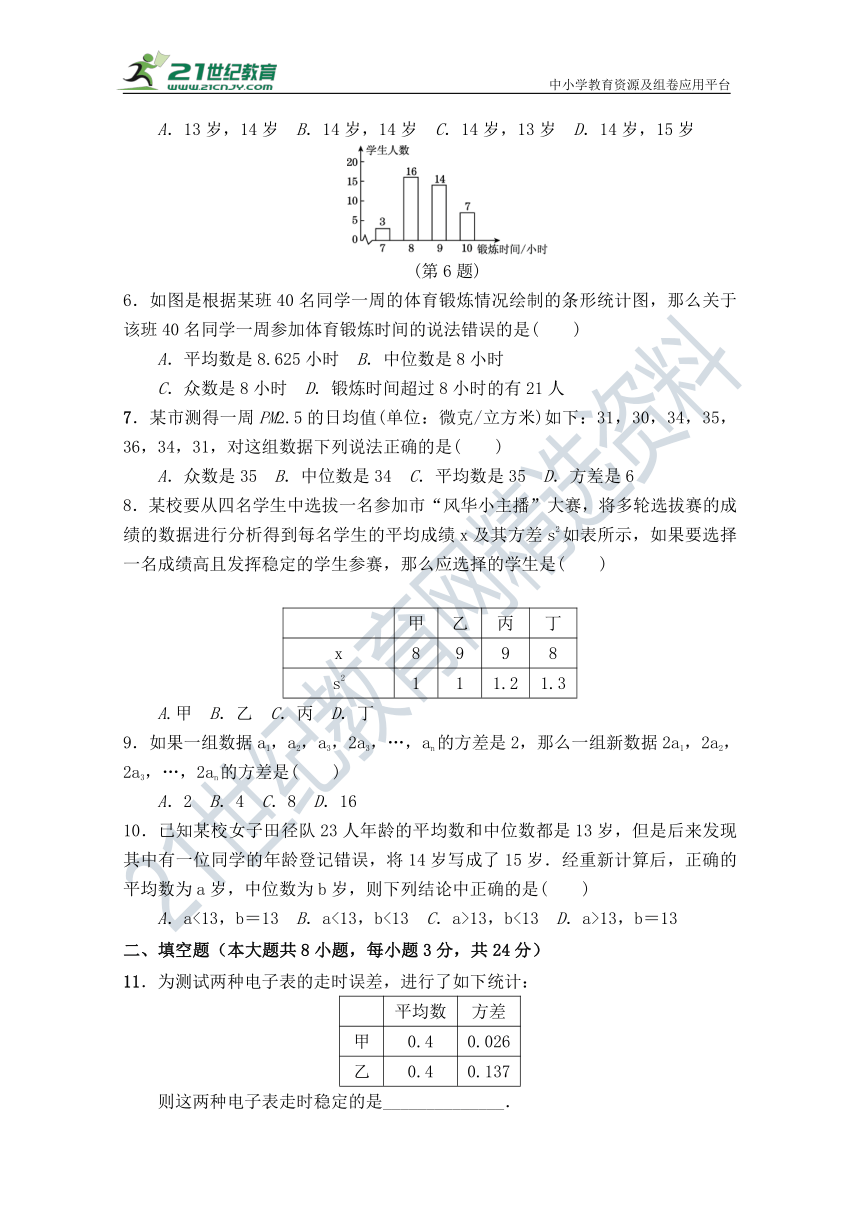
6.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )
A.平均数是8.625小时 B.中位数是8小时
C.众数是8小时 D.锻炼时间超过8小时的有21人
7.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
A.众数是35 B.中位数是34 C.平均数是35 D.方差是6
8.某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如表所示,如果要选择一名成绩高且发挥稳定的学生参赛,那么应选择的学生是( )
甲 乙 丙 丁
x 8 9 9 8
s2 1 1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
9.如果一组数据a1,a2,a3,2a3,…,an的方差是2,那么一组新数据2a1,2a2,2a3,…,2an的方差是( )
A.2 B.4 C.8 D.16
10.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中有一位同学的年龄登记错误,将14岁写成了15岁.经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A.a<13,b=13 B.a<13,b<13 C.a>13,b<13 D.a>13,b=13
二、填空题(本大题共8小题,每小题3分,共24分)
11.为测试两种电子表的走时误差,进行了如下统计:
平均数 方差
甲 0.4 0.026
乙 0.4 0.137
则这两种电子表走时稳定的是______________.
12.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为________.
13.已知一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依次类推,第n个数是n).设这组数据的各数之和是s,中位数是k,则s=________(用只含有k的代数式表示).
14.某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数分布直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5~80.5分这个分数段;④如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
15.对某中学同龄的70名女生的身高进行测量后,得到一组数据,其中最大值为169 cm,最小值为145 cm,对这组数据进行整理后,确定它的组距为2.3 cm,则组数为________.
16.如图是某农场里三种蔬菜种植面积的扇形统计图,若西红柿种植面积为4.2公顷,则这三种蔬菜种植总面积是________公顷,表示黄瓜的扇形圆心角的度数为________.
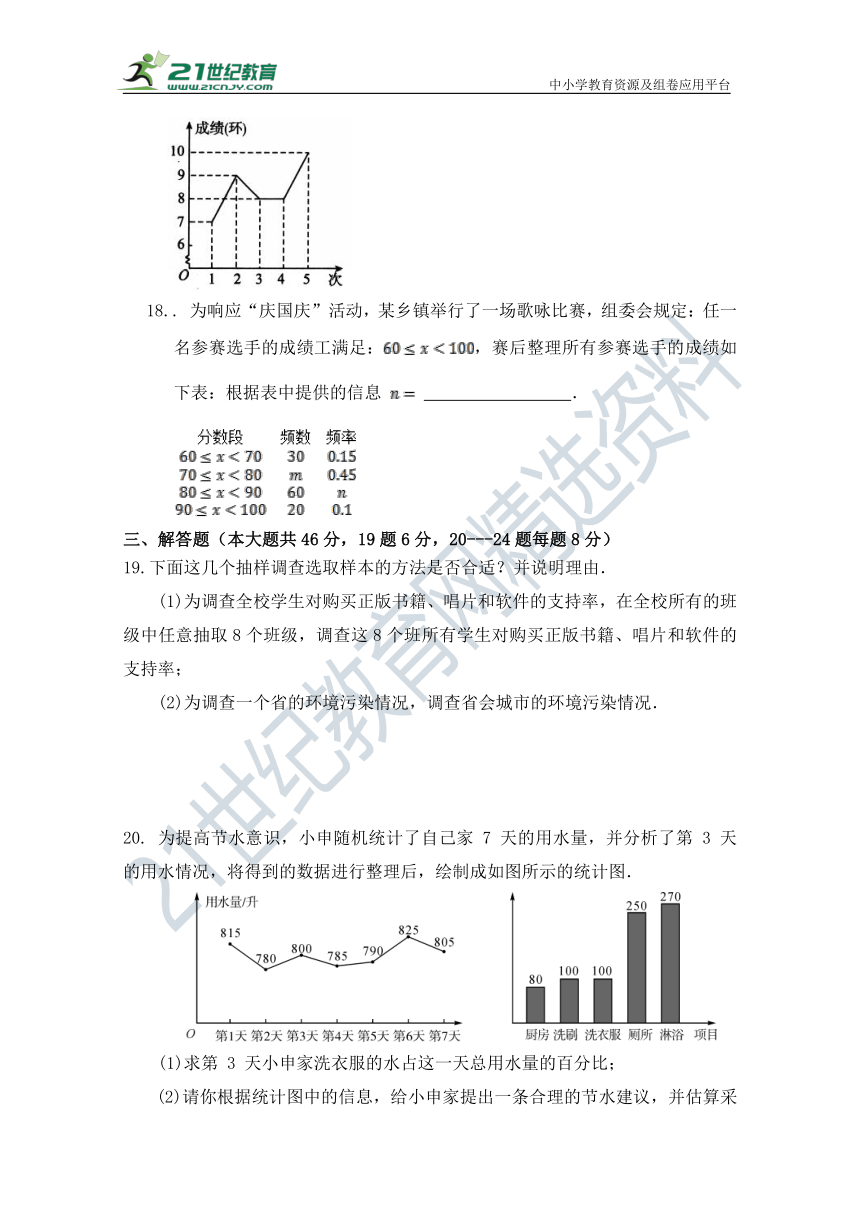
17.如图所示是小敏 次射击成绩的折线图,根据图示信息,这 次成绩的平均数是 环.
18.. 为响应“庆国庆”活动,某乡镇举行了一场歌咏比赛,组委会规定:任一名参赛选手的成绩工满足:,赛后整理所有参赛选手的成绩如下表:根据表中提供的信息 .
三、解答题(本大题共46分,19题6分,20---24题每题8分)
19.下面这几个抽样调查选取样本的方法是否合适?并说明理由.
(1)为调查全校学生对购买正版书籍、唱片和软件的支持率,在全校所有的班级中任意抽取8个班级,调查这8个班所有学生对购买正版书籍、唱片和软件的支持率;
(2)为调查一个省的环境污染情况,调查省会城市的环境污染情况.
20. 为提高节水意识,小申随机统计了自己家 7 天的用水量,并分析了第 3 天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.
(1)求第 3 天小申家洗衣服的水占这一天总用水量的百分比;
(2)请你根据统计图中的信息,给小申家提出一条合理的节水建议,并估算采用你的建议后小申家一个月(按 30 天计算)的节水量..
21.如图是A、B两所学校艺术节期间收到的各类艺术作品的统计图:
(1) 从图中能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
22.某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数.
23.某中学九年级学生在社会实践中,调查了500位市民某天早上出行上班所用的交通工具,结果如下扇形统计图表示.
(1)请你将扇形统计图改成折线统计图;
(2)请根据此项调查,对于城市交通方面给相关部门提出一条建议.
24. 某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品的成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下的统计表和如图9所示的频数分布直方图.
“文明在我身边”摄影比赛成绩统计表
分数段 频数 频率
60≤x<70 18 0.36
70≤x<80 17 c
80≤x<90 a 0.24
90≤x≤100 b 0.06
图9
根据以上信息,解答下列问题:
(1)统计表中,c= ;样本成绩的中位数落在分数段 中.
(2)补全频数分布直方图.
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量.
参考答案:
一.填空题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D B B B B C A
二.选择题
11.甲 点拨:比较统计表中甲、乙方差的大小,方差小的稳定.
126 点拨:由题意得解得
∴这组新数据是3,4,5,6,8,8,8,其中位数是6.
13.2k2-k
14.①③④ 点拨:由题中的频数分布直方图可知,比赛成绩在50.5~60.5分数段的有4人,60.5~70.5分数段的有12人,70.5~80.5分数段的有20人,80.5~90.5分数段的有10人,90.5~100.5分数段的有6人,所以参加比赛的学生共有4+12+20+10+6=52(人),①正确;由已知条件和频数分布直方图得不出比赛成绩为65分的学生人数,②错误;将比赛成绩按从小到大的顺序排列,第26,27个数据都在70.5~80.5分数段内,故比赛成绩的中位数落在70.5~80.5分这个分数段,③正确;如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率为×100%≈30.8%,④正确.
15.11 点拨:(169-145)÷2.3≈10.43,采用进一法确定组数.
16.7.5;108°
17.
18.
三.解答题
19. 解:(1)选取样本方法合适,具有代表性.
(2)选取样本方法不合适,样本缺乏代表性.;
20. 解:(1) ×100%=12.5% .
(2)答案不唯一.例如:可以用洗衣服的水冲厕所.采用该建议,每天大约可以节约用水 100 升,一个月估计可以节约用水 100×30=3 000 升.
21.⑴.不能.因为在只知道各校水粉画作品的百分比而不知道总量的前提下,是不能进行比较的.
⑵设A、B两所学校收到艺术作品的总数分别是x件和y件则解之: 答略.
22. 解:(1)由题意得,E组为(10÷5)×2=4(人),发言人总数为4÷8%=50(人),A组为50×6%=3(人),C组为50×30%=15(人),D组为50×26%=13(人),∴F组为50-3-10-15-13-4=5(人),补全直方图略.
(2)∵在统计的50人中,发言次数不少于12次的有4+5=9(人),∴在这天发言次数不少于12次的频率为=18%,∴全年级500人中,在这天里发言次数不少于12次的人数为500×18%=90(人).
23. 解:(1)步行人数为500×6%=30(人);自行车人数为500×20%=100(人);
电动车人数为500×12%=60(人);公交车人数为500×56%=280(人);私家车人数为500×6%=30(人),改成折线统计图略.
(2)答案不唯一,略.
24. (1)0.34 70≤x<80 (2)略 (3)估计全校被展评的作品数量是180幅.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第十章《数据的收集、整理与描述》单元检测题
题号 一 二 三 总分
21 22 23 24 25 26 27 28
分数
一、选择题(本大题共10小题,每小题3分,共计30分)
1.学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
得分 60 70 80 90 100
人数 7 12 10 8 3
得分的众数和中位数分别是( )
A.70,70 B.80,80 C.70,80 D.80,70
2.某球员参加一场篮球比赛,比赛分4节进行,该球员每节的得分如图1所示,则该球员平均每节的得分为( )
1.
2. 图1
A.7分 B.8分 C.9分 D.10分
一个班有40名学生,在期末体育考核中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是( )
A.144° B.162° C.216° D.250°
4.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
A.4,4 B.3,4 C.4,3 D.3,3
5.济南某中学足球队的18名队员的年龄如下表所示:
年龄/岁 12 13 14 15
人数 3 5 6 4
这18名队员年龄的众数和中位数分别是( )
A.13岁,14岁 B.14岁,14岁 C.14岁,13岁 D.14岁,15岁
(第6题)
6.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )
A.平均数是8.625小时 B.中位数是8小时
C.众数是8小时 D.锻炼时间超过8小时的有21人
7.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
A.众数是35 B.中位数是34 C.平均数是35 D.方差是6
8.某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如表所示,如果要选择一名成绩高且发挥稳定的学生参赛,那么应选择的学生是( )
甲 乙 丙 丁
x 8 9 9 8
s2 1 1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
9.如果一组数据a1,a2,a3,2a3,…,an的方差是2,那么一组新数据2a1,2a2,2a3,…,2an的方差是( )
A.2 B.4 C.8 D.16
10.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中有一位同学的年龄登记错误,将14岁写成了15岁.经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A.a<13,b=13 B.a<13,b<13 C.a>13,b<13 D.a>13,b=13
二、填空题(本大题共8小题,每小题3分,共24分)
11.为测试两种电子表的走时误差,进行了如下统计:
平均数 方差
甲 0.4 0.026
乙 0.4 0.137
则这两种电子表走时稳定的是______________.
12.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为________.
13.已知一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依次类推,第n个数是n).设这组数据的各数之和是s,中位数是k,则s=________(用只含有k的代数式表示).
14.某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数分布直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5~80.5分这个分数段;④如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
15.对某中学同龄的70名女生的身高进行测量后,得到一组数据,其中最大值为169 cm,最小值为145 cm,对这组数据进行整理后,确定它的组距为2.3 cm,则组数为________.
16.如图是某农场里三种蔬菜种植面积的扇形统计图,若西红柿种植面积为4.2公顷,则这三种蔬菜种植总面积是________公顷,表示黄瓜的扇形圆心角的度数为________.
17.如图所示是小敏 次射击成绩的折线图,根据图示信息,这 次成绩的平均数是 环.
18.. 为响应“庆国庆”活动,某乡镇举行了一场歌咏比赛,组委会规定:任一名参赛选手的成绩工满足:,赛后整理所有参赛选手的成绩如下表:根据表中提供的信息 .
三、解答题(本大题共46分,19题6分,20---24题每题8分)
19.下面这几个抽样调查选取样本的方法是否合适?并说明理由.
(1)为调查全校学生对购买正版书籍、唱片和软件的支持率,在全校所有的班级中任意抽取8个班级,调查这8个班所有学生对购买正版书籍、唱片和软件的支持率;
(2)为调查一个省的环境污染情况,调查省会城市的环境污染情况.
20. 为提高节水意识,小申随机统计了自己家 7 天的用水量,并分析了第 3 天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.
(1)求第 3 天小申家洗衣服的水占这一天总用水量的百分比;
(2)请你根据统计图中的信息,给小申家提出一条合理的节水建议,并估算采用你的建议后小申家一个月(按 30 天计算)的节水量..
21.如图是A、B两所学校艺术节期间收到的各类艺术作品的统计图:
(1) 从图中能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
22.某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数.
23.某中学九年级学生在社会实践中,调查了500位市民某天早上出行上班所用的交通工具,结果如下扇形统计图表示.
(1)请你将扇形统计图改成折线统计图;
(2)请根据此项调查,对于城市交通方面给相关部门提出一条建议.
24. 某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品的成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下的统计表和如图9所示的频数分布直方图.
“文明在我身边”摄影比赛成绩统计表
分数段 频数 频率
60≤x<70 18 0.36
70≤x<80 17 c
80≤x<90 a 0.24
90≤x≤100 b 0.06
图9
根据以上信息,解答下列问题:
(1)统计表中,c= ;样本成绩的中位数落在分数段 中.
(2)补全频数分布直方图.
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量.
参考答案:
一.填空题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D B B B B C A
二.选择题
11.甲 点拨:比较统计表中甲、乙方差的大小,方差小的稳定.
126 点拨:由题意得解得
∴这组新数据是3,4,5,6,8,8,8,其中位数是6.
13.2k2-k
14.①③④ 点拨:由题中的频数分布直方图可知,比赛成绩在50.5~60.5分数段的有4人,60.5~70.5分数段的有12人,70.5~80.5分数段的有20人,80.5~90.5分数段的有10人,90.5~100.5分数段的有6人,所以参加比赛的学生共有4+12+20+10+6=52(人),①正确;由已知条件和频数分布直方图得不出比赛成绩为65分的学生人数,②错误;将比赛成绩按从小到大的顺序排列,第26,27个数据都在70.5~80.5分数段内,故比赛成绩的中位数落在70.5~80.5分这个分数段,③正确;如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率为×100%≈30.8%,④正确.
15.11 点拨:(169-145)÷2.3≈10.43,采用进一法确定组数.
16.7.5;108°
17.
18.
三.解答题
19. 解:(1)选取样本方法合适,具有代表性.
(2)选取样本方法不合适,样本缺乏代表性.;
20. 解:(1) ×100%=12.5% .
(2)答案不唯一.例如:可以用洗衣服的水冲厕所.采用该建议,每天大约可以节约用水 100 升,一个月估计可以节约用水 100×30=3 000 升.
21.⑴.不能.因为在只知道各校水粉画作品的百分比而不知道总量的前提下,是不能进行比较的.
⑵设A、B两所学校收到艺术作品的总数分别是x件和y件则解之: 答略.
22. 解:(1)由题意得,E组为(10÷5)×2=4(人),发言人总数为4÷8%=50(人),A组为50×6%=3(人),C组为50×30%=15(人),D组为50×26%=13(人),∴F组为50-3-10-15-13-4=5(人),补全直方图略.
(2)∵在统计的50人中,发言次数不少于12次的有4+5=9(人),∴在这天发言次数不少于12次的频率为=18%,∴全年级500人中,在这天里发言次数不少于12次的人数为500×18%=90(人).
23. 解:(1)步行人数为500×6%=30(人);自行车人数为500×20%=100(人);
电动车人数为500×12%=60(人);公交车人数为500×56%=280(人);私家车人数为500×6%=30(人),改成折线统计图略.
(2)答案不唯一,略.
24. (1)0.34 70≤x<80 (2)略 (3)估计全校被展评的作品数量是180幅.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
